摘要: 在求解线性方程组时,直接解法有顺序高斯消元法、列主元高斯消元法、全主元高斯消元法、高斯约当消元法、消元形式的追赶法、LU分解法、矩阵形式的追赶法,当我们遇到对称正定线性方程组时,我们就要用到平方根法(对称LLT分解法)来求解,为了熟悉和熟练运用平方根法求解线性...
在求解线性方程组时,直接解法有顺序高斯消元法、列主元高斯消元法、全主元高斯消元法、高斯约当消元法、消元形式的追赶法、LU分解法、矩阵形式的追赶法,当我们遇到对称正定线性方程组时,我们就要用到平方根法(对称LLT分解法)来求解,为了熟悉和熟练运用平方根法求解线性方程组,下面对运用平方根法求解线性方程组进行解析。
一、运用平方根法求解线性方程组涉及到的定理及定义 我们在运用平方根法求解线性方程组时,要判定线性方程组Ax=b的系数矩阵A是否是对称正定矩阵,那么我们就要了解正定矩阵的性质和如下定理及定义:
1、由线性代数知,正定矩阵具有如下性质:
1) 正定矩阵A是非奇异的
2) 正定矩阵A的任一主子矩阵也必为正定矩阵
3) 正定矩阵A的主对角元素均为正数
4) 正定矩阵 A的特征值均大于零
5) 正定矩阵A的行列式必为正数 定义一 线性方程组Ax=b的系数矩阵A是对称正定矩阵,那么Ax=b是对称正定线性方程组。 定义二 如果方阵A满足A=AT,那么A是对称阵。
2平方根法和改进的平方根法 如果A是n阶对称矩阵,由定理2还可得如下分解定理:
定理2 若A为n阶对称矩阵,且A的各阶顺序主子式都不为零,则A可惟一分解为:A=LDLT,其中L为单位下三角阵,D为对角阵。
定理3 对称矩阵A为正定的充分必要条件是A的各阶顺序主子式大于零。
2 对称正定矩阵的三角分解
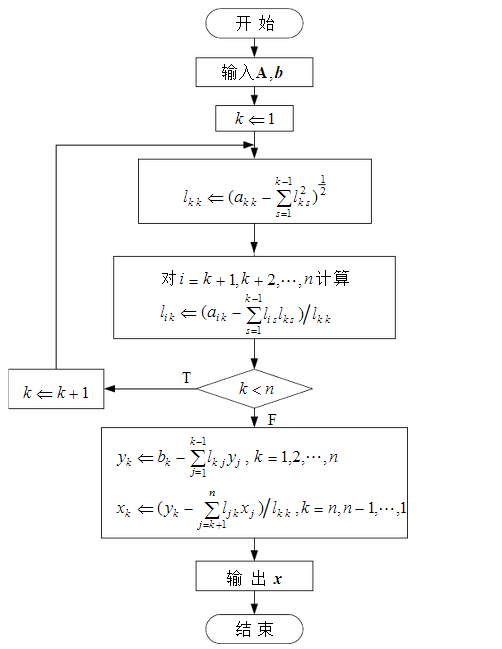
定理 (Cholesky分解)设A为n阶对称正定矩阵,则存在惟一的主对角线元素都是正数的下三角阵L,使得:A=LLT。 分解式A=LLT称为正定矩阵的Cholesky分解,利用Cholesky分解来求解系数矩阵为对称正定矩阵的方程组AX=b的方法称为平方根法。
二、平方根法的算法流程图