几何平均数的定义和公式

几何平均数的定义和公式

几何平均数（geometric mean）是指n个观察值连乘积的n次方根。根据资料的条件不同，几何平均数有加权和不加权之分。中国古代数学书中提到的矩形面积时往往用长宽的几何平均数来表示。

我们知道算术平均数，\( \frac {a+b}{2} \)体现纯粹数字上的关系；

而√[ab]称为几何平均数，这个体现了一个几何关系。

作一正方形，使其面积等于以a,b为长宽的矩形，则该正方形的边长即为a、b的几何平均数。

中国古代数学书中提到的矩形面积时往往用长宽的几何平均数来表示。

公式：

\(X=n√[X1 \times X2 \times X3 \times … \times Xn]\)

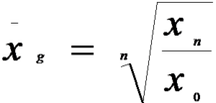
几何平均数的主要用途

计算几何平均数要求各观察值之间存在连乘积关系，它的主要用途是：

1.对比率、指数等进行平均；

2.计算平均发展速度；

其中：样本数据非负，主要用于对数正态分布。

3.复利下的平均年利率；

4.连续作业的车间求产品的平均合格率。