解析算术平均数与调和平均数的关系

平均指标又称统计平均数，用以反映社会经济现象总体各单位某一数量标志在一定时间，地点条件下所达到的一般水平。包括算术平均数、调和平均数、几何平均数、众数和中位数。算术平均数和调和平均数的联系与区别是一大难题，下面就这一问题进行分析。

一、计算公式

算术平均数和社会经济统计中常用的调和平均数均符从以上基本公式，其具体计算公式分别为：

其中：x为各组标志值；权数（对平均指标的大小有权衡轻重影响作用的因素）f为各组单位数；权数m为各组标志总量。

二、算术平均数和调和平均数的关系

从算术平均数和调和平均数常用的计算公式可看出，两者既有区别，又有联系。

（1）两者的联系

第一，算术平均数和调和平均数都满足平均指标的基本公式：

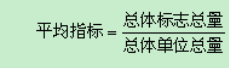
由于在社会经济统计中，调和平均数采用特定形式的权数，即m=xf，所以调和平均数是算术平均数的一种变形，其基本关系式为：

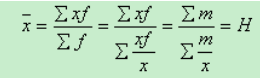
（2）两者的区别

第一，两者所取权数的含义不同。算术平均数的权数f是指各组的单位数或各组单位数占总体单位数的比重；而调和平均数的权数m是指各组的标志总量。

第二，两者的应用条件不同。

如果已知各组职工人数,分母资料，就以各组职工人数为权数f或f/åf，采用算术平均数公式计算。

如果已知各组工资总额，分子资料，就以工资总额为权数m，采用调和平均数公式计算。

所以在已知所求平均数的分子资料时，应以分子资料为权数m，采用调和平均数公式计算。