将位置和速度转换到银河系中心框架和从银河系中心框架转换#
此示例演示如何使用和自定义 Galactocentric 框架将日心天空位置、距离、自行和辐射速度转换为银河心、直角坐标系,反之亦然。
的主要可配置参数 Galactocentric 框架控制银河系内太阳系重心的位置和速度。这些是通过设置银河系中心的ICRS坐标、到银河系中心的距离(太阳-银河中心线始终假设为银河系中心框架的x轴)以及银河系中心框架中太阳的笛卡儿3速度来指定的。我们将首先演示如何自定义这些值,然后演示如何通过输入Sgr A* 的自行来设置太阳运动。
请注意,为了简洁起见,我们可以在下面的例子中将太阳系重心称为“太阳”。
让我们首先定义ICRS框架中的重心坐标和速度。我们将使用来自 Simbad 数据库:
>>> import astropy.coordinates as coord
>>> from astropy import units as u
>>> c1 = coord.SkyCoord(
... ra=89.014303 * u.degree,
... dec=13.924912 * u.degree,
... distance=(37.59 * u.mas).to(u.pc, u.parallax()),
... pm_ra_cosdec=372.72 * (u.mas / u.yr),
... pm_dec=-483.69 * (u.mas / u.yr),
... radial_velocity=0.37 * (u.km / u.s),
... frame="icrs",
... )
这是一颗高自行恒星;假设我们想将其位置和速度转换为银河系中心框架,看看它是否也具有很大的3D速度。要使用Astropy默认太阳位置和运动参数,我们可以执行以下操作:
>>> gc1 = c1.transform_to(coord.Galactocentric)
从这里,我们可以访问结果的组件 Galactocentric 实例以查看3D Cartesian速度分量:
>>> print(gc1.v_x, gc1.v_y, gc1.v_z)
30.254684717897074 km / s 171.29916086104885 km / s 18.19390627095307 km / s
的默认参数 Galactocentric 链接文档中详细介绍了框架,但我们可以使用关键字修改最常更改的值 galcen_distance , galcen_v_sun ,而且 z_sun 它们分别设置太阳与银河系中心距离、太阳的3D速度载体以及太阳在银河系中平面上方的高度。太阳的速度可以指定为 Quantity 具有速度单位的对象,并被解释为Cartesian速度,如下例所示。请注意,与位置一样,银河系中心框架是右手系统(即,太阳处于负x值)所以 v_x 与银河系中心辐射速度相反:
>>> v_sun = [11.1, 244, 7.25] * (u.km / u.s) # [vx, vy, vz]
>>> gc_frame = coord.Galactocentric(
... galcen_distance=8 * u.kpc, galcen_v_sun=v_sun, z_sun=0 * u.pc
... )
然后我们可以使用自定义参数转换到这个帧:
>>> gc2 = c1.transform_to(gc_frame)
>>> print(gc2.v_x, gc2.v_y, gc2.v_z)
28.427958360720748 km / s 169.69916086104888 km / s 17.70831652451455 km / s
使用指定太阳运动有时很有用 proper motion of Sgr A* 而不是笛卡儿速度分量。通过假设的距离,我们可以使用以下方法将自行分量转换为Cartesian速度分量 astropy.units :
>>> galcen_distance = 8 * u.kpc
>>> pm_gal_sgrA = [-6.379, -0.202] * (u.mas / u.yr) # from Reid & Brunthaler 2004
>>> vy, vz = -(galcen_distance * pm_gal_sgrA).to(u.km / u.s, u.dimensionless_angles())
我们仍然必须假设银河系中心的视线速度,我们将再次采取11公里/秒:
>>> vx = 11.1 * (u.km / u.s)
>>> v_sun2 = u.Quantity([vx, vy, vz]) # List of Quantity -> a single Quantity
>>> gc_frame2 = coord.Galactocentric(
... galcen_distance=galcen_distance, galcen_v_sun=v_sun2, z_sun=0 * u.pc
... )
>>> gc3 = c1.transform_to(gc_frame2)
>>> print(gc3.v_x, gc3.v_y, gc3.v_z)
28.427958360720748 km / s 167.61484955608267 km / s 18.118916793584443 km / s
转换也朝着相反的方向进行。这对于将模拟或理论数据转换为可观察量非常有用。例如,我们将生成4个具有相同圆速度、不同银河中心半径的理论圆轨道,并将它们转换为日心坐标:
>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> import astropy.coordinates as coord
>>> from astropy import units as u
>>> ring_distances = np.arange(10, 26, 5) * u.kpc
>>> circ_velocity = 220 * (u.km / u.s)
>>> phi_grid = np.linspace(90, 270, 512) * u.degree # grid of azimuths
>>> ring_rep = coord.CylindricalRepresentation(
... rho=ring_distances[:, np.newaxis],
... phi=phi_grid[np.newaxis],
... z=np.zeros_like(ring_distances)[:, np.newaxis],
... )
>>> angular_velocity = (-circ_velocity / ring_distances).to(
... u.mas / u.yr, u.dimensionless_angles()
... )
>>> ring_dif = coord.CylindricalDifferential(
... d_rho=np.zeros(phi_grid.shape)[np.newaxis] * (u.km / u.s),
... d_phi=angular_velocity[:, np.newaxis],
... d_z=np.zeros(phi_grid.shape)[np.newaxis] * (u.km / u.s),
... )
>>> ring_rep = ring_rep.with_differentials(ring_dif)
>>> gc_rings = coord.SkyCoord(ring_rep, frame=coord.Galactocentric)
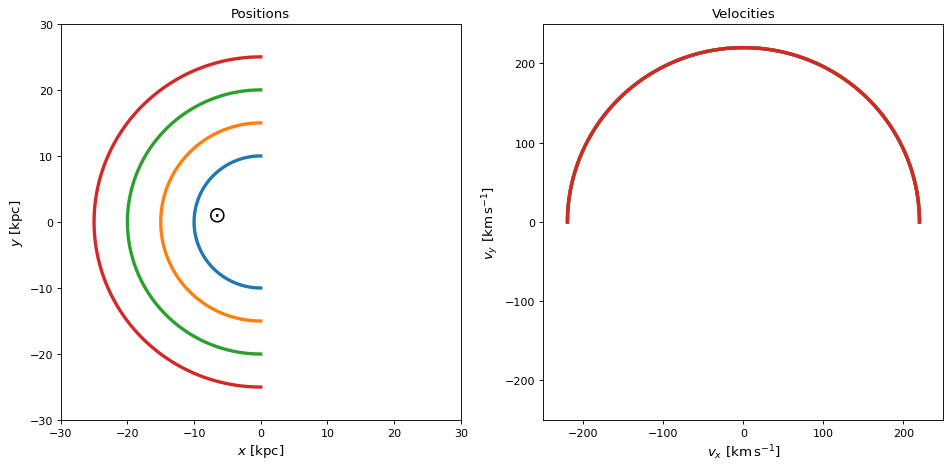
首先,让我们可视化银河系中心坐标中的几何形状。以下是环的位置和速度;请注意,在速度图中,4个环的速度相同,因此重叠在同一条曲线下:
>>> fig, axes = plt.subplots(1, 2, figsize=(12, 6))
>>> axes[0].plot(gc_rings.x.T, gc_rings.y.T, marker="None", linewidth=3)
>>> axes[0].text(-8.0, 0, r"$\odot$", fontsize=20)
>>> axes[0].set_xlim(-30, 30)
>>> axes[0].set_ylim(-30, 30)
>>> axes[0].set_xlabel("$x$ [kpc]")
>>> axes[0].set_ylabel("$y$ [kpc]")
>>> axes[0].set_title("Positions")
>>> axes[1].plot(gc_rings.v_x.T, gc_rings.v_y.T, marker="None", linewidth=3)
>>> axes[1].set_xlim(-250, 250)
>>> axes[1].set_ylim(-250, 250)
>>> axes[1].set_xlabel(f"$v_x$ [{(u.km / u.s).to_string('latex_inline')}]")
>>> axes[1].set_ylabel(f"$v_y$ [{(u.km / u.s).to_string('latex_inline')}]")
>>> axes[1].set_title("Velocities")
>>> fig.tight_layout()
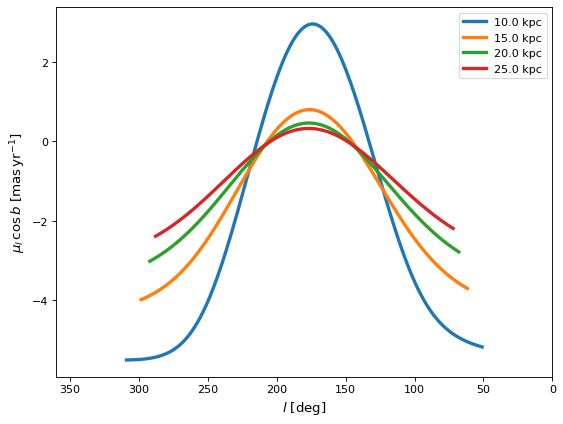
现在我们可以转换到银河系坐标并在可观测坐标中可视化环:
>>> gal_rings = gc_rings.transform_to(coord.Galactic)
>>> fig, ax = plt.subplots(1, 1, figsize=(8, 6))
>>> for i in range(len(ring_distances)):
... ax.plot(
... gal_rings[i].l.degree,
... gal_rings[i].pm_l_cosb.value,
... label=str(ring_distances[i]),
... marker="None",
... linewidth=3,
... )
>>> ax.set_xlim(360, 0)
>>> ax.set_xlabel("$l$ [deg]")
>>> ax.set_ylabel(rf'$\mu_l \, \cos b$ [{(u.mas/u.yr).to_string("latex_inline")}]')
>>> ax.legend()
>>> plt.draw()