使用角度#
各种坐标对象的角度分量由 Angle 班级。虽然最有可能在坐标对象的上下文中遇到, Angle 在需要角度表示的地方,对象也可以单独使用。
创造#
创建 Angle 对象非常灵活,支持多种输入对象类型和格式。数组的类型可以是标量,数组的类型可以是, Quantity 或者别的什么 Angle . 这一点最好用一些创建 Angle .
实例#
有多种方法可以创建 Angle ::
>>> import numpy as np
>>> from astropy import units as u
>>> from astropy.coordinates import Angle
>>> Angle('10.2345d') # String with 'd' abbreviation for degrees
<Angle 10.2345 deg>
>>> Angle(['10.2345d', '-20d']) # Array of strings
<Angle [ 10.2345, -20. ] deg>
>>> Angle('1:2:30.43 degrees') # Sexagesimal degrees
<Angle 1.04178611 deg>
>>> Angle('1 2 0 hours') # Sexagesimal hours
<Angle 1.03333333 hourangle>
>>> Angle(np.arange(1., 8.), unit=u.deg) # Numpy array from 1..7 in degrees
<Angle [1., 2., 3., 4., 5., 6., 7.] deg>
>>> Angle('1°2′3″') # Unicode degree, arcmin and arcsec symbols
<Angle 1.03416667 deg>
>>> Angle('1°2′3″N') # Unicode degree, arcmin, arcsec symbols and direction
<Angle 1.03416667 deg>
>>> Angle('1d2m3.4s') # Degree, arcmin, arcsec.
<Angle 1.03427778 deg>
>>> Angle('1d2m3.4sS') # Degree, arcmin, arcsec, direction.
<Angle -1.03427778 deg>
>>> Angle('-1h2m3s') # Hour, minute, second
<Angle -1.03416667 hourangle>
>>> Angle('-1h2m3sW') # Hour, minute, second, direction
<Angle 1.03416667 hourangle>
>>> Angle(10.2345 * u.deg) # From a Quantity object in degrees
<Angle 10.2345 deg>
>>> Angle(Angle(10.2345 * u.deg)) # From another Angle object
<Angle 10.2345 deg>
表现#
这个 Angle 对象还支持多种表示角度值的方法,既可以是浮点数,也可以是字符串。
实例#
有许多方法可以表示 Angle ::
>>> a = Angle(1, u.radian)
>>> a
<Angle 1. rad>
>>> a.radian
1.0
>>> a.degree
57.29577951308232
>>> a.hour
3.8197186342054885
>>> a.hms
hms_tuple(h=3.0, m=49.0, s=10.987083139758766)
>>> a.dms
dms_tuple(d=57.0, m=17.0, s=44.806247096362313)
>>> a.signed_dms
signed_dms_tuple(sign=1.0, d=57.0, m=17.0, s=44.806247096362313)
>>> (-a).dms
dms_tuple(d=-57.0, m=-17.0, s=-44.806247096362313)
>>> (-a).signed_dms
signed_dms_tuple(sign=-1.0, d=57.0, m=17.0, s=44.806247096362313)
>>> a.arcminute
3437.7467707849396
>>> f"{a}"
'1.0 rad'
>>> f"{a:latex}"
'$1\\;\\mathrm{rad}$'
>>> f"{a.to(u.deg):latex}"
'$57^\\circ17{}^\\prime44.8062471{}^{\\prime\\prime}$'
>>> a.to_string()
'1 rad'
>>> a.to_string(unit=u.degree)
'57d17m44.8062471s'
>>> a.to_string(unit=u.degree, sep=':')
'57:17:44.8062471'
>>> a.to_string(unit=u.degree, sep=('deg', 'm', 's'))
'57deg17m44.8062471s'
>>> a.to_string(unit=u.hour)
'3h49m10.98708314s'
>>> a.to_string(unit=u.hour, decimal=True)
'3.81972'
使用#
对于适当的算术运算,角度也会表现正确。
例子#
使用 Angle 算术运算中的对象:
>>> a = Angle(1.0, u.radian)
>>> a + 0.5 * u.radian + 2 * a
<Angle 3.5 rad>
>>> np.sin(a / 2)
<Quantity 0.47942554>
>>> a == a
array(True, dtype=bool)
>>> a == (a + a)
array(False, dtype=bool)
Angle 对象也可用于创建坐标对象。
例子#
使用 Angle ::
>>> from astropy.coordinates import ICRS
>>> ICRS(Angle(1, u.deg), Angle(0.5, u.deg))
<ICRS Coordinate: (ra, dec) in deg
(1., 0.5)>
包装和边界#
有两种实用方法用于处理应该有边界的角度。这个 wrap_at() 方法允许获取一个或多个角度,并将其包装在单个360度切片内。这个 is_within_bounds() 方法返回一个布尔值,指示一个或多个角度是否在指定的边界内。
备注
在创建时 Angle 具有整型数据类型的数组的实例在技术上是可能的(例如,使用 dtype=int ),它的功能非常有限,尤其是不支持对此类对象进行包装。
经纬度对象#
Longitude 和 Latitude 是 Angle 类,该类用于所有球坐标类。 Longitude 用于表示诸如赤经、银河经度和方位角等值(分别表示赤道坐标、银河坐标和Alt-Az坐标)。 Latitude 用于赤纬、星系纬度和仰角。
经度#
A Longitude 物体不同于纯粹的 Angle 凭借 wrap_angle 属性。这个 wrap_angle 指定对象表示的所有角度值都在以下范围内:
wrap_angle - 360 * u.deg <= angle(s) < wrap_angle
默认值 wrap_angle 是360度设置 'wrap_angle=180 * u.deg' 会导致值介于-180和+180度之间。设置 wrap_angle 现有的属性 Longitude 将重新放置对象的角度值。例如::
>>> from astropy.coordinates import Longitude
>>> a = Longitude([-20, 150, 350, 360] * u.deg)
>>> a.degree
array([340., 150., 350., 0.])
>>> a.wrap_angle = 180 * u.deg
>>> a.degree
array([-20., 150., -10., 0.])
纬度#
纬度物体不同于纯物体 Angle 由于受到约束而:
-90.0 * u.deg <= angle(s) <= +90.0 * u.deg
任何试图设置超出该范围的值都将导致 ValueError .
生成角度值#
Astropy提供了用于通过随机采样或值栅格生成角度或球面位置的实用函数。这些函数都返回 BaseRepresentation 子类实例,可以直接传递到坐标框类或 SkyCoord 创建随机或栅格坐标对象。
使用随机抽样#
这两个函数都使用标准、随机 spherical point picking 以生成在单位球体的表面上均匀分布的角度位置。若要仅检索角度值,请使用 uniform_spherical_random_surface 。例如,要生成4个随机角度位置:
>>> from astropy.coordinates import uniform_spherical_random_surface
>>> pts = uniform_spherical_random_surface(size=4)
>>> pts
<UnitSphericalRepresentation (lon, lat) in rad
[(0.52561028, 0.38712031), (0.29900285, 0.52776066),
(0.98199282, 0.34247723), (2.15260367, 1.01499232)]>
若要在由最大半径设置的球形体积内均匀生成三维位置,请改用 uniform_spherical_random_volume 功能。例如,要生成4个随机3D位置:
>>> from astropy.coordinates import uniform_spherical_random_volume
>>> pts_3d = uniform_spherical_random_volume(size=4)
>>> pts_3d
<SphericalRepresentation (lon, lat, distance) in (rad, rad, )
[(4.98504602, -0.74247419, 0.39752416),
(5.53281607, 0.89425191, 0.7391255 ),
(0.88100456, 0.21080555, 0.5531785 ),
(6.00879324, 0.61547168, 0.61746148)]>
默认情况下,返回的距离值在单位球体内均匀分布(即,距离值是无量纲的)。要在给定维度半径的球体内生成随机点(例如,1秒),请传入 Quantity 属性的对象 max_radius 论点::
>>> import astropy.units as u
>>> pts_3d = uniform_spherical_random_volume(size=4, max_radius=2*u.pc)
>>> pts_3d
<SphericalRepresentation (lon, lat, distance) in (rad, rad, pc)
[(3.36590297, -0.23085809, 1.47210093),
(6.14591179, 0.06840621, 0.9325143 ),
(2.19194797, 0.55099774, 1.19294064),
(5.25689272, -1.17703409, 1.63773358)]>
在网格上#
球体上的任何网格或点阵都不能在所有网格点之间产生相等的间距,但是存在许多近似算法来生成具有几乎均匀间距的角度网格(例如, see this page )。
在这种情况下,一种简单而流行的方法是 golden spiral method ,可在 astropy.coordinates 通过实用程序函数 golden_spiral_grid 。此函数接受单个参数, size ,它指定要在网格中生成的点数:
>>> from astropy.coordinates import golden_spiral_grid
>>> golden_pts = golden_spiral_grid(size=32)
>>> golden_pts
<UnitSphericalRepresentation (lon, lat) in rad
[(1.94161104, 1.32014066), (5.82483312, 1.1343273 ),
(3.42486989, 1.004232 ), (1.02490666, 0.89666582),
(4.90812873, 0.80200278), (2.5081655 , 0.71583806),
(0.10820227, 0.63571129), (3.99142435, 0.56007531),
(1.59146112, 0.48787515), (5.4746832 , 0.41834639),
(3.07471997, 0.35090734), (0.67475674, 0.28509644),
(4.55797882, 0.22053326), (2.15801559, 0.15689287),
(6.04123767, 0.09388788), (3.64127444, 0.03125509),
(1.24131121, -0.03125509), (5.12453328, -0.09388788),
(2.72457005, -0.15689287), (0.32460682, -0.22053326),
(4.2078289 , -0.28509644), (1.80786567, -0.35090734),
(5.69108775, -0.41834639), (3.29112452, -0.48787515),
(0.89116129, -0.56007531), (4.77438337, -0.63571129),
(2.37442014, -0.71583806), (6.25764222, -0.80200278),
(3.85767899, -0.89666582), (1.45771576, -1.004232 ),
(5.34093783, -1.1343273 ), (2.9409746 , -1.32014066)]>
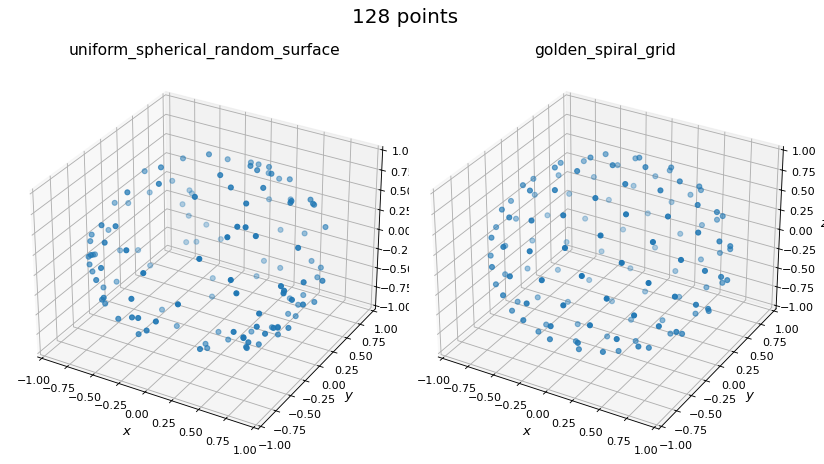
球点生成方法的比较#