使用SkyCoord高级课程#
这个 SkyCoord 类为天体坐标表示、操作和坐标系之间的转换提供了一个简单而灵活的用户界面。这是一个高级类,作为底层坐标系类的包装器,例如 ICRS 和 FK5 他们承担了大部分的重担。
两者之间的主要区别 SkyCoord 低层阶级 (坐标系的使用与设计 )具体如下:
这个
SkyCoord对象可以维护中所有内置和用户定义的坐标系的帧属性的并集astropy.coordinates.frame_transform_graph. 单个帧类只保存该帧所需的属性(例如,春分点、观测时间或观察者位置)。这意味着FK4(有春分和观测时间)到ICRS(既没有)又回到FK4通过低层班不会记得原来的春分和观测时间。自从SkyCoord对象存储所有属性,这样的往返转换将返回到同一个坐标对象。这个
SkyCoord类在输入方面更加灵活,以适应各种用户首选项和可用的数据格式,而Frame类期望接收具有角度单位的类似数量的对象。这个
SkyCoord类具有许多在典型分析中有用的方便方法。目前,
SkyCoord对象只能使用在astropy.coordinates.frame_transform_graph变换图形对象。
创建SkyCoord对象#
这个 SkyCoord 类接受各种各样的输入进行初始化。至少,这些必须提供一个或多个具有明确单位的天体坐标值。通常还必须指定坐标系,但这不是必需的。
常见模式如下所示。在这个描述中,大写的值如下 COORD 或 FRAME 表示在中详细描述的输入 Initialization Syntax 第节。方括号中的元素 [unit=UNIT] 是可选的。:
SkyCoord(COORD, [FRAME], keyword_args ...)
SkyCoord(LON, LAT, [frame=FRAME], [unit=UNIT], keyword_args ...)
SkyCoord([FRAME], <lon_attr>=LON, <lat_attr>=LAT, keyword_args ...)
下面的示例说明初始化 SkyCoord 对象。这些都反映了使用球坐标进行初始化,这是所有内置帧的默认设置。要了解使用不同表示法(如笛卡尔坐标或圆柱坐标)处理坐标,请参见 Representations . 首先,一些进口商品:
>>> from astropy.coordinates import SkyCoord # High-level coordinates
>>> from astropy.coordinates import ICRS, Galactic, FK4, FK5 # Low-level frames
>>> from astropy.coordinates import Angle, Latitude, Longitude # Angles
>>> import astropy.units as u
>>> import numpy as np
实例#
坐标值和帧规范可以使用位置参数和关键字参数提供。首先,我们展示了RA和Dec的位置参数:
>>> SkyCoord(10, 20, unit='deg') # Defaults to ICRS
<SkyCoord (ICRS): (ra, dec) in deg
(10., 20.)>
>>> SkyCoord([1, 2, 3], [-30, 45, 8], frame='icrs', unit='deg')
<SkyCoord (ICRS): (ra, dec) in deg
[(1., -30.), (2., 45.), (3., 8.)]>
请注意,上面的第一个示例没有显式地给出一个框架。在这种情况下,默认设置为ICRS系统(对于“J2000”赤道坐标,该系统大致正确)。然而,当已知帧是icr时,最好显式地指定它,因为任何阅读代码的人都能够更好地理解其意图。
通用格式的字符串输入是可以接受的,框架可以作为类类型提供,比如 FK4 ,一个框架类的实例,一个 SkyCoord 实例(将从中提取帧)或作为字符串的帧名称的小写版本,例如, "fk4" ::
>>> coords = ["1:12:43.2 +1:12:43", "1 12 43.2 +1 12 43"]
>>> sc = SkyCoord(coords, frame=FK4, unit=(u.hourangle, u.deg), obstime="J1992.21")
>>> sc = SkyCoord(coords, frame=FK4(obstime="J1992.21"), unit=(u.hourangle, u.deg))
>>> sc = SkyCoord(coords, frame='fk4', unit='hourangle,deg', obstime="J1992.21")
>>> sc = SkyCoord("1h12m43.2s", "+1d12m43s", frame=Galactic) # Units from strings
>>> sc = SkyCoord("1h12m43.2s +1d12m43s", frame=Galactic) # Units from string
>>> sc = SkyCoord(l="1h12m43.2s", b="+1d12m43s", frame='galactic')
>>> sc = SkyCoord("1h12.72m +1d12.71m", frame='galactic')
请注意,使用数据和 SkyCoord 实例只能作为使用 frame= 关键字参数而不是位置参数。
对于具有 ra 和 dec 属性可以提供其他多种常用格式的坐标字符串。示例包括:
>>> sc = SkyCoord("15h17+89d15")
>>> sc = SkyCoord("275d11m15.6954s+17d59m59.876s")
>>> sc = SkyCoord("8 00 -5 00.6", unit=(u.hour, u.deg))
>>> sc = SkyCoord("J080000.00-050036.00", unit=(u.hour, u.deg))
>>> sc = SkyCoord("J1874221.31+122328.03", unit=u.deg)
阿谀奉承 Quantity -可接受并鼓励将类型对象作为输入形式:
>>> ra = Longitude([1, 2, 3], unit=u.deg) # Could also use Angle
>>> dec = np.array([4.5, 5.2, 6.3]) * u.deg # Astropy Quantity
>>> sc = SkyCoord(ra, dec, frame='icrs')
>>> sc = SkyCoord(ra=ra, dec=dec, frame=ICRS, obstime='2001-01-02T12:34:56')
最后,可以从低级坐标系对象初始化。
>>> c = FK4(1 * u.deg, 2 * u.deg)
>>> sc = SkyCoord(c, obstime='J2010.11', equinox='B1965') # Override defaults
这里突出显示的一个关键微妙之处是,当创建低级对象时,它们具有某些默认属性值。例如 FK4 帧使用 equinox='B1950.0 和 obstime=equinox 作为默认值。如果此对象用于初始化 SkyCoord 可以重写未显式设置的低级对象属性。如果上面的坐标是用 c = FK4(1 * u.deg, 2 * u.deg, equinox='B1960') 然后创建一个 SkyCoord 用不同的 equinox 会引发一个例外。
初始化语法#
对于最常见的球形表示,它是所有内置帧的默认输入格式,其语法 SkyCoord 如下所示:
SkyCoord(COORD, [FRAME | frame=FRAME], [unit=UNIT], keyword_args ...)
SkyCoord(LON, LAT, [DISTANCE], [FRAME | frame=FRAME], [unit=UNIT], keyword_args ...)
SkyCoord([FRAME | frame=FRAME], <lon_name>=LON, <lat_name>=LAT, [unit=UNIT],
keyword_args ...)
在上述描述中,所有大写字母的元素(例如。, FRAME )描述该元素类型的用户输入。方括号中的元素是可选的。有关非球形输入,请参见 Representations 部分。
Lon,LAT#
经度和纬度值可以指定为单独的位置参数。以下选项可用于经度和纬度:
单角度值:
列出或
Quantity数组,或角度值的NumPy数组
备注
同时 SkyCoord 在指定经度和纬度分量输入方面是灵活的,帧类期望接收 Quantity -比如有角度单位的物体(例如。, Angle 或 Quantity ). 例如,在指定组件时,框架类(例如。, ICRS )必须创建为
>>> ICRS(0 * u.deg, 0 * u.deg)
<ICRS Coordinate: (ra, dec) in deg
(0., 0.)>
以及其他灵活的初始化方法(使用 SkyCoord )行不通
>>> ICRS(0, 0, unit=u.deg)
UnitTypeError: Longitude instances require units equivalent to 'rad', but no unit was given.
DISTANCE#
可以选择指定从帧中心到对象的距离:
COORD#
此输入表单使用单个对象来提供坐标数据。对于球面坐标系,坐标可以包括一个或多个经纬度对,方法如下:
单坐标字符串,LON和LAT值用空格分隔。相应的值可以是格式化为的任何字符串 创造 属于
Longitude或Latitude对象。这种坐标字符串的列表或NumPy数组。
(LON,LAT)元组的列表,其中每个LON和LAT都是标量(不是数组)。
N x 2NumPy或Quantity值数组,其中第一列是经度,第二列是纬度,例如,[[270, -30], [355, +85]] * u.deg.(LON,LAT,DISTANCE)元组的列表。
N x 3NumPy或Quantity值数组,其中列分别是经度、纬度和距离。
输入也可以是不一定用标准球坐标表示的更通用的对象:
坐标框对象(例如。,
FK4(1*u.deg, 2*u.deg, obstime='J2012.2'))SkyCoord对象(只复制对象)。BaseRepresentation类对象类SphericalRepresentation,CylindricalRepresentation或CartesianRepresentation.
FRAME
这可能是一个 BaseCoordinateFrame 框架类,此类的实例,或相应的字符串别名。Astropy内置的框架类是 ICRS , FK5 , FK4 , FK4NoETerms , Galactic 和 AltAz . 字符串别名是类名的小写版本。
如果没有提供框架,您将看到一个特殊的 ICRS 标识符。这表示未指定帧,并且不允许进行需要比较坐标(即使在该对象内)的操作。
unit=UNIT
单位说明符可以是以下值之一:
Unit对象,它是一个角度单位,相当于Unit('radian').具有有效角度单位名称的单个字符串。
2元组
Unit对象或字符串单元名称,分别指定LON和LAT单位(例如。,('hourangle', 'degree'))一个字符串,两个单元名用逗号隔开(例如。,
'hourangle,degree')
如果只提供一个单元,则它同时适用于LON和LAT。
其他关键字参数
与指定经度和纬度的位置参数不同,帧特定的名称可以用作关键字参数:
- ra , dec : LON , LAT 值,可选
RA和Dec表示帧,包括 [FIXME]
ICRS,FK5,FK4和FK4NoETerms.- l , b : LON , LAT 值,可选
银河系
l和b对于Galactic框架。
可以为任何帧指定以下关键字:
- distance :类似距离的数量,可选
从中心到源的参考距离
- obstime :像时间一样,可选
观察时间
- equinox :像时间一样,可选
坐标系分点
如果自定义用户定义的帧包含在变换图中,并且它们具有其他帧属性,则也可以通过 SkyCoord 初始化。
阵列操作#
可以将坐标数组存储在 SkyCoord 对象,并且以这种方式进行的操作将比在单个列表上循环快几个数量级 SkyCoord 物体。
实例#
将坐标数组存储在 SkyCoord 对象:
>>> ra = np.linspace(0, 36000, 1001) * u.deg
>>> dec = np.linspace(-90, 90, 1001) * u.deg
>>> sc_list = [SkyCoord(r, d, frame='icrs') for r, d in zip(ra, dec)]
>>> timeit sc_gal_list = [c.galactic for c in sc_list]
1 loops, best of 3: 20.4 s per loop
>>> sc = SkyCoord(ra, dec, frame='icrs')
>>> timeit sc_gal = sc.galactic
100 loops, best of 3: 21.8 ms per loop
除了矢量化转换之外,您还可以使用与用于相同的方法和属性来执行常见的数组切片、分割和选择 ndarray 实例。相应的函数,以及影响形状的其他函数,例如 atleast_1d 和 rollaxis ,如预期般工作。(相关功能必须在中明确启用 astropy 源代码;如果一个 numpy 不支持您认为应该起作用的函数。)::
>>> north_mask = sc.dec > 0
>>> sc_north = sc[north_mask]
>>> len(sc_north)
500
>>> sc[2:4]
<SkyCoord (ICRS): (ra, dec) in deg
[( 72., -89.64), (108., -89.46)]>
>>> sc[500]
<SkyCoord (ICRS): (ra, dec) in deg
(0., 0.)>
>>> sc[0:-1:100].reshape(2, 5)
<SkyCoord (ICRS): (ra, dec) in deg
[[(0., -90.), (0., -72.), (0., -54.), (0., -36.), (0., -18.)],
[(0., 0.), (0., 18.), (0., 36.), (0., 54.), (0., 72.)]]>
>>> np.roll(sc[::100], 1)
<SkyCoord (ICRS): (ra, dec) in deg
[(0., 90.), (0., -90.), (0., -72.), (0., -54.), (0., -36.),
(0., -18.), (0., 0.), (0., 18.), (0., 36.), (0., 54.),
(0., 72.)]>
请注意,与 ndarray 方法,除了 flatten 尝试使用新的数据视图,只有在不可能的情况下才复制数据(如NumPy文档中所讨论的那样) reshape() )
在位修改坐标对象#
数组中的坐标值 SkyCoord 对象可以就地修改(在Astropy4.1中添加)。这需要从另一个 SkyCoord 对象,除了实际的坐标数据值外,在所有方面都是等效的。这样,不需要帧转换,并且项目设置操作非常健壮。
具体来说,右手 value 必须与要修改的对象严格一致:
同级
等效框架 (
is_equivalent_frame)相同的表示类型
相同表示法差分键
相同的帧属性
相同的“额外”帧属性(例如。,
obstime对于ICRS坐标)
修改 SkyCoord 对象对numpy数组使用相同的语法:
>>> sc1 = SkyCoord([1, 2] * u.deg, [3, 4] * u.deg)
>>> sc2 = SkyCoord(10 * u.deg, 20 * u.deg)
>>> sc1[0] = sc2
>>> sc1
<SkyCoord (ICRS): (ra, dec) in deg
[(10., 20.), ( 2., 4.)]>
可以插入标量或数组值 SkyCoord 对象转换为另一个兼容的 SkyCoord 对象:
>>> sc1 = SkyCoord([1, 2] * u.deg, [3, 4] * u.deg)
>>> sc2 = SkyCoord(10 * u.deg, 20 * u.deg)
>>> sc1.insert(1, sc2)
<SkyCoord (ICRS): (ra, dec) in deg
[( 1., 3.), (10., 20.), ( 2., 4.)]>
能够修改 SkyCoord 对象就位,所有 表操作 例如,连接、堆叠和插入都与 SkyCoord 混合柱(只要不需要掩蔽)。
这些方法相对较慢,因为它们需要从现有的 SkyCoord 对象,并执行广泛的验证以确保操作有效。对于某些应用程序,可能需要采用本节中描述的不同的较低级别方法 坐标的快速在位修改 .
警告
例如,您可能会尝试一种显而易见的方法,通过直接更新组件属性来就地修改坐标对象 sc1.ra[1] = 40 * u.deg . 然而,虽然这会 出现 为了给出正确的结果,它实际上并不修改底层表示数据。这与基于性能的缓存的当前实现有关。当前的缓存实现同样无法处理对表示的就地更改 (.data )或帧属性,例如 .obstime .
属性#
这个 SkyCoord 对象有许多有用的属性,这些属性非常有用。通过挖掘这些,我们将了解一点 SkyCoord 以及它的工作原理。
首先,学习对象属性和方法的最重要工具之一是“TAB discovery”。在IPython中,您可以键入对象名称、句点,然后按<TAB>键查看可用的内容。这通常比阅读文档要快:
>>> sc = SkyCoord(1, 2, frame='icrs', unit='deg', obstime='2013-01-02 14:25:36')
>>> sc.<TAB>
sc.T sc.match_to_catalog_3d
sc.altaz sc.match_to_catalog_sky
sc.barycentrictrueecliptic sc.name
sc.cartesian sc.ndim
sc.cirs sc.obsgeoloc
sc.copy sc.obsgeovel
sc.data sc.obstime
sc.dec sc.obswl
sc.default_representation sc.position_angle
sc.diagonal sc.precessedgeocentric
sc.distance sc.pressure
sc.equinox sc.ra
sc.fk4 sc.ravel
sc.fk4noeterms sc.realize_frame
sc.fk5 sc.relative_humidity
sc.flatten sc.represent_as
sc.frame sc.representation_component_names
sc.frame_attributes sc.representation_component_units
sc.frame_specific_representation_info sc.representation_info
sc.from_name sc.reshape
sc.from_pixel sc.roll
sc.galactic sc.search_around_3d
sc.galactocentric sc.search_around_sky
sc.galcen_distance sc.separation
sc.gcrs sc.separation_3d
sc.geocentrictrueecliptic sc.shape
sc.get_constellation sc.size
sc.guess_from_table sc.spherical
sc.has_data sc.spherical_offsets_to
sc.hcrs sc.squeeze
sc.heliocentrictrueecliptic sc.supergalactic
sc.icrs sc.swapaxes
sc.info sc.take
sc.is_equivalent_frame sc.temperature
sc.is_frame_attr_default sc.to_pixel
sc.is_transformable_to sc.to_string
sc.isscalar sc.transform_to
sc.itrs sc.transpose
sc.location sc.z_sun
这里我们看到许多属性和方法。最容易识别的可能是经度和纬度属性,它们被命名为 ra 和 dec 对于 ICRS 框架:
>>> sc.ra
<Longitude 1. deg>
>>> sc.dec
<Latitude 2. deg>
接下来,请注意所有的内置框架名称 icrs , galactic , fk5 , fk4 和 fk4noeterms 有。通过Python属性的魔力,访问这些属性调用对象 transform_to 方法,并返回一个新的 SkyCoord 请求帧中的对象::
>>> sc_gal = sc.galactic
>>> sc_gal
<SkyCoord (Galactic): (l, b) in deg
(99.63785528, -58.70969293)>
您可能认识到的其他属性包括 distance , equinox , obstime 和 shape .
深入调查#
[[普通用户可以跳过此部分]]
在转换为银河系之后,经度和纬度值现在被标记 l 和 b ,遵循银河系坐标的常规。对象如何知道如何调用其值?答案在于一些不那么明显的特征:
>>> sc_gal.representation_component_names
{'l': 'lon', 'b': 'lat', 'distance': 'distance'}
>>> sc_gal.representation_component_units
{'l': Unit("deg"), 'b': Unit("deg")}
>>> sc_gal.representation_type
<class 'astropy.coordinates...SphericalRepresentation'>
它们一起告诉物体 l 和 b 是经度和纬度,它们都应以度为单位显示为球形坐标(而不是笛卡尔坐标)。此外,框架的 representation_component_names 属性定义的坐标关键字参数 SkyCoord 会接受的。
另一个重要属性是 frame_attributes ,它定义了完全定义框架所需的其他属性:
>>> sc_fk4 = SkyCoord(1, 2, frame='fk4', unit='deg')
>>> sc_fk4.frame_attributes
{'equinox': <...TimeAttribute ...>, 'obstime': <...TimeAttribute ...>}
此示例显示, FK4 Frame具有两个属性, equinox 和 obstime ,这是完全定义帧所需的。
这里发生了一些诡计,因为这些属性中的许多实际上是由底层坐标所拥有的 frame 对象,它执行大部分实际工作。这是三层对象系统中的中间层:表示(球形、笛卡尔等)、框架(又称底层框架类)和 SkyCoord (又称高级班;见 概述 astropy.coordinates 概念 和 重要定义 ):
>>> sc.frame
<ICRS Coordinate: (ra, dec) in deg
(1., 2.)>
>>> sc.has_data is sc.frame.has_data
True
>>> sc.frame.<TAB>
sc.frame.T sc.frame.ra
sc.frame.cartesian sc.frame.ravel
sc.frame.copy sc.frame.realize_frame
sc.frame.data sc.frame.represent_as
sc.frame.dec sc.frame.representation
sc.frame.default_representation sc.frame.representation_component_names
sc.frame.diagonal sc.frame.representation_component_units
sc.frame.distance sc.frame.representation_info
sc.frame.flatten sc.frame.reshape
sc.frame.frame_attributes sc.frame.separation
sc.frame.frame_specific_representation_info sc.frame.separation_3d
sc.frame.has_data sc.frame.size
sc.frame.is_equivalent_frame sc.frame.spherical
sc.frame.is_frame_attr_default sc.frame.squeeze
sc.frame.is_transformable_to sc.frame.swapaxes
sc.frame.isscalar sc.frame.take
sc.frame.name sc.frame.transform_to
sc.frame.ndim sc.frame.transpose
>>> sc.frame.name
'icrs'
这个 SkyCoord 对象公开 frame 对象属性。虽然一开始看起来有点困惑,但这是件好事,因为它使 SkyCoord 对象和 BaseCoordinateFrame 对象的行为非常相似,大多数例程都可以接受其中一个作为输入,而无需太多麻烦(duck typing!)。
堆栈中最底层是抽象层 UnitSphericalRepresentation 对象:
>>> sc_gal.frame.data
<UnitSphericalRepresentation (lon, lat) in rad
(1.73900863, -1.02467744)>
变换#
转换的主题在 系统间转换 .
为了完整起见,我们将给出一些例子。一旦定义了坐标和参考坐标系,就可以从该坐标系变换到另一坐标系。您可以用几种不同的方法来实现这一点:如果只需要该帧的默认版本,则可以使用属性样式访问(如前所述)。为了获得更多的控制,可以使用 transform_to 方法,它接受框架名称、框架类、框架实例或 SkyCoord .
实例#
从一帧转换到另一帧:
>>> from astropy.coordinates import FK5
>>> sc = SkyCoord(1, 2, frame='icrs', unit='deg')
>>> sc.galactic
<SkyCoord (Galactic): (l, b) in deg
(99.63785528, -58.70969293)>
>>> sc.transform_to('fk5') # Same as sc.fk5 and sc.transform_to(FK5)
<SkyCoord (FK5: equinox=J2000.000): (ra, dec) in deg
(1.00000656, 2.00000243)>
>>> sc.transform_to(FK5(equinox='J1975')) # Transform to FK5 with a different equinox
<SkyCoord (FK5: equinox=J1975.000): (ra, dec) in deg
(0.67967282, 1.86083014)>
转换为 SkyCoord 实例是确保两个坐标处于完全相同的参考坐标系中的一种方便方法:
>>> sc2 = SkyCoord(3, 4, frame='fk4', unit='deg', obstime='J1978.123', equinox='B1960.0')
>>> sc.transform_to(sc2)
<SkyCoord (FK4: equinox=B1960.000, obstime=J1978.123): (ra, dec) in deg
(0.48726331, 1.77731617)>
陈述#
到目前为止,我们在所有的示例中都使用了球形坐标表示,这是内置框架的默认值。通常,使用笛卡尔或圆柱等不同的表示形式初始化或使用坐标很方便。在本节中,我们将讨论如何使用不同的表示来初始化对象,以及如何更改对象的表示。有关表示对象本身的详细信息,请参见 使用和设计坐标表示法 .
初始化#
您需要知道的大部分内容都可以从下面的示例中推断出来,也可以通过推断之前的球面表示文档来推断。初始化需要设置 representation_type 关键字,并为该表示形式提供相应的组件。
实例#
要使用非球形的表示类型初始化对象,请执行以下操作:
>>> c = SkyCoord(x=1, y=2, z=3, unit='kpc', representation_type='cartesian')
>>> c
<SkyCoord (ICRS): (x, y, z) in kpc
(1., 2., 3.)>
>>> c.x, c.y, c.z
(<Quantity 1. kpc>, <Quantity 2. kpc>, <Quantity 3. kpc>)
其他变化包括:
>>> SkyCoord(1, 2*u.deg, 3, representation_type='cylindrical')
<SkyCoord (ICRS): (rho, phi, z) in (, deg, )
(1., 2., 3.)>
>>> SkyCoord(rho=1*u.km, phi=2*u.deg, z=3*u.m, representation_type='cylindrical')
<SkyCoord (ICRS): (rho, phi, z) in (km, deg, m)
(1., 2., 3.)>
>>> SkyCoord(rho=1, phi=2, z=3, unit=(u.km, u.deg, u.m), representation_type='cylindrical')
<SkyCoord (ICRS): (rho, phi, z) in (km, deg, m)
(1., 2., 3.)>
>>> SkyCoord(1, 2, 3, unit=(None, u.deg, None), representation_type='cylindrical')
<SkyCoord (ICRS): (rho, phi, z) in (, deg, )
(1., 2., 3.)>
一般来说,允许的语法如下:
SkyCoord(COORD, [FRAME | frame=FRAME], [unit=UNIT], [representation_type=REPRESENTATION],
keyword_args ...)
SkyCoord(COMP1, COMP2, [COMP3], [FRAME | frame=FRAME], [unit=UNIT],
[representation_type=REPRESENTATION], keyword_args ...)
SkyCoord([FRAME | frame=FRAME], <comp1_name>=COMP1, <comp2_name>=COMP2,
<comp3_name>=COMP3, [representation_type=REPRESENTATION], [unit=UNIT],
keyword_args ...)
在这种情况下, keyword_args 现在包括元素 representation_type=REPRESENTATION . 在上述描述中,所有大写字母的元素(例如。, FRAME )描述该元素类型的用户输入。方括号中的元素是可选的。
组件1 , 组件2 , 组件3
组件值可以指定为单独的位置参数或关键字参数。在这种形式中,允许输入的确切类型取决于表示的细节。通常,支持以下输入表单:
单一值:
组件类对象
纯数值
unit指定单位的关键字
列表或组件类数组,或数值数组
每个表示组件都有一个指定的类(“组件类”),用于将通用输入数据转换为具有特定单位的预定义对象类。这些组件类应该是 Quantity 班级。
COORD
此输入表单使用单个对象来提供坐标数据。坐标可以指定一个或多个坐标位置,如下所示:
名单
(COMP1, .., COMP<M>)元组,其中每个组件都是标量(不是数组),并且M表示中的组件。通常有三种成分,但有些成分(例如。,UnitSphericalRepresentation)可以少一些。N x MNumPy或Quantity值数组,其中N是坐标和M是组件的数量。
REPRESENTATION
该表示形式可以作为 BaseRepresentation 类(例如, CartesianRepresentation )或作为字符串名,它只是小写的类名,不带 'representation' 后缀(例如, 'cartesian' )。
用于创建 SkyCoord 一般情况下的对象与球形对象相同。
细节#
可用的表示集是动态的,可能会根据定义的表示类进行更改。内置表示法包括:
名字 |
等级 |
|---|---|
|
|
|
|
|
|
|
|
|
每个帧都知道所有可用的表示法,但不同的帧可能对相同的组件使用不同的名称。一个常见的例子是 Galactic 帧使用 l 和 b 而不是 ra 和 dec 对于 lon 和 lat 的组件 SphericalRepresentation .
对于一个特定的框架,为了查看表示的完整列表以及它如何命名所有组件,首先创建一个没有任何数据的框架实例,然后打印 representation_info 属性:
>>> ICRS().representation_info
{astropy.coordinates...CartesianRepresentation:
{'names': ('x', 'y', 'z'),
'units': (None, None, None)},
astropy.coordinates...SphericalRepresentation:
{'names': ('ra', 'dec', 'distance'),
'units': (Unit("deg"), Unit("deg"), None)},
astropy.coordinates...UnitSphericalRepresentation:
{'names': ('ra', 'dec'),
'units': (Unit("deg"), Unit("deg"))},
astropy.coordinates...PhysicsSphericalRepresentation:
{'names': ('phi', 'theta', 'r'),
'units': (Unit("deg"), Unit("deg"), None)},
astropy.coordinates...CylindricalRepresentation:
{'names': ('rho', 'phi', 'z'),
'units': (None, Unit("deg"), None)}
}
这有点混乱,但它表明对于每个表示都有一个 dict 有两个键:
names:定义如何在该框架中命名每个组件。units:定义输出时每个组件的单位,其中None意思是不强迫一个特定的单位。
对于特定的坐标实例,可以使用 representation_type 属性与 representation_component_names 属性来计算特定类对象接受哪些关键字。前者是表示系统的表示类(例如赤道框架的球形表示),后者是将该框架的名称映射到表示类上组件名称的字典:
>>> import astropy.units as u
>>> icrs = ICRS(1*u.deg, 2*u.deg)
>>> icrs.representation_type
<class 'astropy.coordinates...SphericalRepresentation'>
>>> icrs.representation_component_names
{'ra': 'lon', 'dec': 'lat', 'distance': 'distance'}
改变表象#
可以更改坐标对象的表示,如下所示。这确实是 没有什么 存储坐标值的对象内部数据,但它以两种方式更改该数据的外部视图:
这个物体按照新的表示法打印自己。
可用属性将更改以匹配新表示形式的属性(例如,从
ra, dec, distance到x, y, z)
设置 representation_type 从而改变了 属性 在不改变代表三维空间中一个点的内在对象本身的情况下(它是如何出现的)。
实例#
通过设置 representation_type ::
>>> c = SkyCoord(x=1, y=2, z=3, unit='kpc', representation_type='cartesian')
>>> c
<SkyCoord (ICRS): (x, y, z) in kpc
(1., 2., 3.)>
>>> c.representation_type = 'cylindrical'
>>> c
<SkyCoord (ICRS): (rho, phi, z) in (kpc, deg, kpc)
(2.23606798, 63.43494882, 3.)>
>>> c.phi.to(u.deg)
<Angle 63.43494882 deg>
>>> c.x
Traceback (most recent call last):
...
AttributeError: 'SkyCoord' object has no attribute 'x'
>>> c.representation_type = 'spherical'
>>> c
<SkyCoord (ICRS): (ra, dec, distance) in (deg, deg, kpc)
(63.43494882, 53.3007748, 3.74165739)>
>>> c.representation_type = 'unitspherical'
>>> c
<SkyCoord (ICRS): (ra, dec) in deg
(63.43494882, 53.3007748)>
也可以使用任何表示类来设置表示:
>>> from astropy.coordinates import CartesianRepresentation
>>> c.representation_type = CartesianRepresentation
请注意,如果您只需要一个特定的表示而不更改 SkyCoord 对象,则应改为使用 astropy.coordinates.SkyCoord.represent_as() 方法:
>>> c.representation_type = 'spherical'
>>> cart = c.represent_as(CartesianRepresentation)
>>> cart
<CartesianRepresentation (x, y, z) in kpc
(1., 2., 3.)>
>>> c.representation_type
<class 'astropy.coordinates...SphericalRepresentation'>
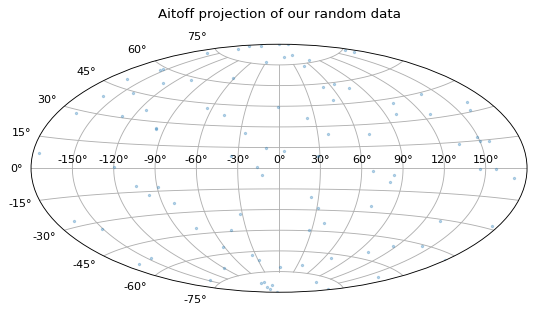
例1:在Aitoff投影中绘制随机数据#
这是一个如何在Aitoff投影中使用 SkyCoord 对象。这里,将使用随机生成的数据集。
首先我们需要导入所需的包。我们使用 matplotlib 在这里策划和 numpy 得到pi值并生成随机数据。
>>> from astropy import units as u
>>> from astropy.coordinates import SkyCoord
>>> import numpy as np
我们现在生成随机数据进行可视化。对于RA,这是在0到360度范围内完成的 (ra_random ),适用于-90度和+90度之间的DEC (dec_random ). 最后,我们将这些值乘以度数得到 Quantity 以度为单位。
>>> rng = np.random.default_rng()
>>> ra_random = rng.uniform(0, 360, 100) * u.degree
>>> dec_random = rng.uniform(-90, 90, 100) * u.degree
As the next step, those coordinates are transformed into an
astropy.coordinates SkyCoord object.
>>> c = SkyCoord(ra=ra_random, dec=dec_random, frame='icrs')
因为matplotlib需要以弧度表示的坐标 \(-\pi\) 和 \(\pi\) ,不是0和 \(2\pi\) ,我们必须转换它们。为此目的 astropy.coordinates.Angle 对象提供了一个特殊的方法,我们在这里用它来包装180:
>>> ra_rad = c.ra.wrap_at(180 * u.deg).radian
>>> dec_rad = c.dec.radian
最后一步,我们用matplotlib设置绘图环境,使用Aitoff投影(具有特定标题、网格、填充圆作为标记,标记大小为2,alpha值为0.3)。我们使用一个x-y比率的图形,它非常适合这样的投影,我们将标题从其通常的位置向上移动,以避免与轴标签重叠。
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(figsize=(8, 4.2), subplot_kw=dict(projection="aitoff"))
>>> ax.title("Aitoff projection of our random data")
>>> ax.grid(True)
>>> ax.scatter(ra_rad, dec_rad, marker="o", s=2, alpha=0.3)
>>> fig.subplots_adjust(top=0.95, bottom=0.0)
>>> plt.show()
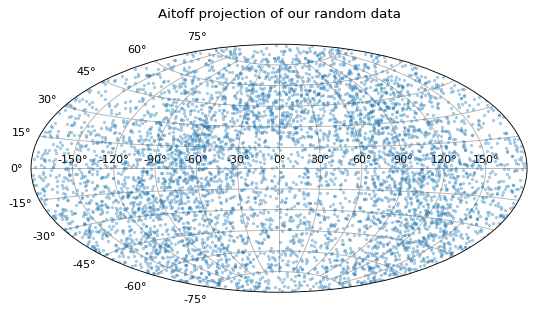
示例2:绘制凸起和圆盘中的星形位置#
这是一个更现实的例子,说明如何使用 SkyCoord 对象。在这里,我们将使用一个随机生成的数据集(多元正态分布)来描述星系中的两颗恒星。两种类型都将以不同的计数绘制。
与上一个示例一样,我们首先导入所需的包。
>>> from astropy import units as u
>>> from astropy.coordinates import SkyCoord
>>> import numpy as np
现在,我们使用以下工具生成用于可视化的随机数据 numpy.random.Generator.multivariate_normal 。
>>> rng = np.random.default_rng()
>>> disk = rng.multivariate_normal(mean=[0,0,0], cov=np.diag([1,1,0.5]), size=5000)
>>> bulge = rng.multivariate_normal(mean=[0,0,0], cov=np.diag([1,1,1]), size=500)
>>> galaxy = np.concatenate([disk, bulge])
As the next step, those coordinates are transformed into an
astropy.coordinates SkyCoord object.
>>> c_gal = SkyCoord(galaxy, representation_type='cartesian', frame='galactic')
>>> c_gal_icrs = c_gal.icrs
同样,与上一个示例一样,我们需要以弧度转换坐标,并确保它们介于 \(-\pi\) 和 \(\pi\) :
>>> ra_rad = c_gal_icrs.ra.wrap_at(180 * u.deg).radian
>>> dec_rad = c_gal_icrs.dec.radian
我们使用与上一个示例相同的打印设置:
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(figsize=(8, 4.2), subplot_kw=dict(projection="aitoff"))
>>> ax.set_title("Aitoff projection of our random data")
>>> ax.grid(True)
>>> ax.scatter(ra_rad, dec_rad, marker="o", s=2, alpha=0.3)
>>> fig.subplots_adjust(top=0.95, bottom=0.0)
>>> plt.show()
比较SkyCoord对象#
有两种主要的比较方法 SkyCoord 互相反对。首先是检查坐标是否在彼此指定的距离内。这是大多数用户在科学或处理分析工作中应该做的,因为它允许由于浮点表示问题而产生的公差。第二个是检查两个对象的精确等价性,这对于编写测试的开发人员非常有用。
下面的示例说明了使用精确相等比较的浮点问题,其中我们进行往返转换FK4=>ICRS=>FK4,然后进行比较:
>>> sc1 = SkyCoord(1*u.deg, 2*u.deg, frame='fk4')
>>> sc1.icrs.fk4 == sc1
np.False_
公差内匹配#
若要测试坐标是否在彼此之间的某个角度距离内,请使用 separation() 方法:
>>> sc1.icrs.fk4.separation(sc1).to(u.arcsec)
<Angle 7.98873629e-13 arcsec>
>>> sc1.icrs.fk4.separation(sc1) < 1e-9 * u.arcsec
np.True_
完全相等#
Astropy还为坐标提供了精确的相等运算符。例如,当比较时,例如两个 SkyCoord 物体::
>>> left_skycoord == right_skycoord
右对象必须与左对象严格一致,以便比较:
同级
等效框架 (
is_equivalent_frame)相同的表示类型
相同表示法差分键
相同的帧属性
相同的“额外”帧属性(例如。,
obstime对于ICRS坐标)
在第一个示例中,我们展示了使用数组值坐标进行的简单比较:
>>> sc1 = SkyCoord([1, 2]*u.deg, [3, 4]*u.deg)
>>> sc2 = SkyCoord([1, 20]*u.deg, [3, 4]*u.deg)
>>> sc1 == sc2 # Array-valued comparison
array([ True, False])
>>> sc2 == sc2[1] # Broadcasting comparison with a scalar
array([False, True])
>>> sc2[0] == sc2[1] # Scalar to scalar comparison
np.False_
>>> sc1 != sc2 # Not equal
array([False, True])
除了在数值上比较表示组件数据(可能包括速度),等式比较还包括所有帧属性都喜欢的严格测试 equinox 或 obstime 完全相等。属性中的任何不匹配都将导致引发异常。例如::
>>> sc1 = SkyCoord([1, 2]*u.deg, [3, 4]*u.deg)
>>> sc2 = SkyCoord([1, 20]*u.deg, [3, 4]*u.deg, obstime='2020-01-01')
>>> sc1 == sc2
...
ValueError: cannot compare: extra frame attribute 'obstime' is not equivalent
(perhaps compare the frames directly to avoid this exception)
在这个例子中, obstime 属性是所谓的“额外”帧属性,不直接应用于ICRS坐标系。所以我们可以和下面的比较,这次使用 != 品种操作员:
>>> sc1.frame != sc2.frame
array([False, True])
一个稍微特殊的情况是比较两个都没有数据的帧,其中返回值与 frame1.is_equivalent_frame(frame2) . 例如::
>>> from astropy.coordinates import FK4
>>> FK4() == FK4(obstime='2020-01-01')
False
将SkyCoord转换为表格#
A SkyCoord 对象可以转换为 QTable 使用ITS to_table() 方法。对象的属性 SkyCoord 转换为表的列或添加到表的元数据中,具体取决于它们是否与 SkyCoord 。这意味着属性,如 obstime 可以成为列或元数据::
>>> from astropy.coordinates import SkyCoord
>>> from astropy.time import Time
>>> sc = SkyCoord(ra=[15, 30], dec=[-70, -50], unit=u.deg,
... obstime=Time([2000, 2010], format='jyear'))
>>> t = sc.to_table()
>>> t
<QTable length=2>
ra dec obstime
deg deg
float64 float64 Time
------- ------- -------
15.0 -70.0 2000.0
30.0 -50.0 2010.0
>>> t.meta
{'representation_type': 'spherical', 'frame': 'icrs'}
>>> sc = SkyCoord(l=[0, 20], b=[20, 0], unit=u.deg, frame='galactic',
... obstime=Time(2000, format='jyear'))
>>> t = sc.to_table()
>>> t
<QTable length=2>
l b
deg deg
float64 float64
------- -------
0.0 20.0
20.0 0.0
>>> t.meta
{'representation_type': 'spherical', 'frame': 'galactic',
'obstime': <Time object: scale='tt' format='jyear' value=2000.0>}
方便方法#
提供了许多方便的方法,建议您阅读以下可用的docstring:
有关其他信息和示例,请参见 分隔、偏移、目录匹配和相关功能 和 空间运动的解释 .

