多维图像处理 (scipy.ndimage )

引言

图像处理和分析通常被视为对二维值数组的操作。然而，有许多领域必须对高维图像进行分析。医学成像和生物成像就是很好的例子。 numpy 由于其固有的多维性质，非常适合这种类型的应用。这个 scipy.ndimage Packages提供了许多常规图像处理和分析函数，这些函数旨在与任意维数的数组一起操作。该软件包目前包括：用于线性和非线性滤波、二进制形态学、B样条插值和对象测量的函数。

所有函数共享的属性

所有函数都有一些共同的属性。值得注意的是，所有函数都允许使用 输出 论点。使用此参数，您可以指定一个数组，该数组将随操作的结果就地更改。在这种情况下，不返回结果。通常，使用 输出 参数的效率更高，因为使用现有数组存储结果。

返回的数组类型取决于操作的类型，但在大多数情况下，它等于输入的类型。但是，如果 输出 参数，则结果的类型等于指定的输出参数的类型。如果没有给出输出参数，仍然可以指定输出的结果。这只需将所需的 numpy 在输出参数中键入Object。例如：

>>> from scipy.ndimage import correlate
>>> correlate(np.arange(10), [1, 2.5])
array([ 0,  2,  6,  9, 13, 16, 20, 23, 27, 30])
>>> correlate(np.arange(10), [1, 2.5], output=np.float64)
array([  0. ,   2.5,   6. ,   9.5,  13. ,  16.5,  20. ,  23.5,  27. ,  30.5])

过滤函数

本节中描述的函数都对输入数组执行某种类型的空间过滤：输出中的元素是相应输入元素附近的值的某个函数。我们将这种元素的邻域称为过滤内核，它的形状通常是矩形的，但也可能具有任意的占用空间。下面描述的许多函数允许您通过将掩码传递给 占地面积 参数。例如，十字形内核可以定义如下：

>>> footprint = np.array([[0, 1, 0], [1, 1, 1], [0, 1, 0]])
>>> footprint
array([[0, 1, 0],
       [1, 1, 1],
       [0, 1, 0]])

通常，核的原点在中心，计算方法是将核形状的维度除以2。例如，长度为3的一维核的原点在第二个元素。例如，以一维阵列与长度为3的过滤的相关性为例，该过滤由1组成：

>>> from scipy.ndimage import correlate1d
>>> a = [0, 0, 0, 1, 0, 0, 0]
>>> correlate1d(a, [1, 1, 1])
array([0, 0, 1, 1, 1, 0, 0])

有时，为内核选择不同的原点会很方便。因此，大多数函数都支持 原点 参数，该参数提供过滤相对于其中心的原点。例如：

>>> a = [0, 0, 0, 1, 0, 0, 0]
>>> correlate1d(a, [1, 1, 1], origin = -1)
array([0, 1, 1, 1, 0, 0, 0])

其效果是结果向左移动。不会经常需要此功能，但它可能会很有用，特别是对于大小相等的过滤器。一个很好的例子是计算向后和向前的差异：

>>> a = [0, 0, 1, 1, 1, 0, 0]
>>> correlate1d(a, [-1, 1])               # backward difference
array([ 0,  0,  1,  0,  0, -1,  0])
>>> correlate1d(a, [-1, 1], origin = -1)  # forward difference
array([ 0,  1,  0,  0, -1,  0,  0])

我们也可以按如下方式计算远期差额：

>>> correlate1d(a, [0, -1, 1])
array([ 0,  1,  0,  0, -1,  0,  0])

但是，使用Origin参数而不是使用更大的内核会更有效。对于多维内核， 原点 可以是一个数字，在这种情况下，假定原点沿所有轴相等，也可以是沿每个轴给出原点的序列。

由于输出元素是输入元素附近元素的函数，因此需要通过提供边界外的值来适当处理数组的边界。这是通过假设根据某些边界条件将数组扩展到其边界之外来实现的。在下面描述的函数中，可以使用 mode 参数，该参数必须是具有边界条件名称的字符串。当前支持以下边界条件：

mode

description

example

“最近”

使用边界处的值

[1 2 3] -> [1 1 2 3 3]

“包裹”

定期复制阵列

[1 2 3] -> [3 1 2 3 1]

“反思”

在边界处反射阵列

[1 2 3] -> [1 1 2 3 3]

“镜子”

在边界镜像阵列

[1 2 3] -> [2 1 2 3 2]

“常量”

使用常量值，默认值为0.0

[1 2 3] -> [0%1%2%3%0]

为了与插值例程保持一致，还支持以下同义词：

mode

description

“网格常数”

相当于“常量”*

“网格镜”

相当于“反映”

“网格换行”

相当于“包装”

*“网格常数”和“常数”在滤波操作中是等价的，但在插值函数中具有不同的行为。为保证API一致性，过滤函数接受任一名称。

“常量”模式是特殊的，因为它需要一个额外的参数来指定应该使用的常量值。

请注意，镜像模式和反射模式的不同之处仅在于是否在反射时重复边界上的采样。对于模式镜像，对称点正好在最终采样处，因此值不会重复。此模式也称为整体样本对称，因为对称点落在最终样本上。类似地，反射通常指的是半样本对称，因为对称点是阵列边界之外的半样本。

注解

实现此类边界条件的最简单方法是将数据复制到更大的数组中，并根据边界条件在边界处扩展数据。对于大型数组和大型过滤内核，这将非常消耗内存，因此下面描述的函数使用不需要分配大型临时缓冲区的不同方法。

相关和卷积

  • 这个 correlate1d 函数计算沿给定轴的一维相关性。沿给定轴的阵列直线与给定的 重量 。这个 重量 参数必须是一维数字序列。

  • 该函数 correlate 实现输入数组与给定内核的多维关联。

  • 这个 convolve1d 函数沿给定轴计算一维卷积。沿给定轴的阵列直线与给定的 重量 。这个 重量 参数必须是一维数字序列。

  • 该函数 convolve 实现具有给定内核的输入数组的多维卷积。

    注解

    卷积本质上是镜像内核之后的相关性。因此， 原点 参数的行为与关联的情况不同：结果以相反的方向移动。

平滑过滤器

  • 这个 gaussian_filter1d 函数实现一维高斯过滤。高斯过滤的标准差通过参数传递 西格玛 。设置 订单 =0对应于高斯核的卷积。1、2或3的阶数对应于与高斯的一阶、二阶或三阶导数的卷积。不实现更高阶导数。

  • 这个 gaussian_filter 函数实现了一个多维高斯过滤。高斯过滤沿每个轴的标准差通过参数传递 西格玛 作为序列或数字。如果 西格玛 不是序列而是单个数字，过滤的标准差在各个方向都是相等的。过滤的顺序可以分别为每个轴指定。阶数为0对应于与高斯核的卷积。1、2或3的阶数对应于与高斯的一阶、二阶或三阶导数的卷积。不实现更高阶导数。这个 订单 参数必须是数字，才能为所有轴指定相同的顺序，或者必须是数字序列，才能为每个轴指定不同的顺序。

    注解

    多维过滤被实现为一维高斯滤波器序列。中间数组以与输出相同的数据类型存储。因此，对于精度较低的输出类型，结果可能不精确，因为中间结果的存储精度可能不够高。这可以通过指定更精确的输出类型来防止。

  • 这个 uniform_filter1d 函数计算给定对象的一维均匀过滤 size 沿着给定的轴线。

  • 这个 uniform_filter 实现多维统一过滤。对于每个轴，统一过滤的大小以整数序列的形式由 size 参数。如果 size 不是序列，而是单个数字，则假定沿所有轴的大小相等。

    注解

    多维过滤被实现为一维均匀滤波器序列。中间数组以与输出相同的数据类型存储。因此，对于精度较低的输出类型，结果可能不精确，因为中间结果的存储精度可能不够高。这可以通过指定更精确的输出类型来防止。

基于顺序统计量的过滤器

  • 这个 minimum_filter1d 函数计算给定对象的一维最小过滤 size 沿着给定的轴线。

  • 这个 maximum_filter1d 函数计算给定对象的一维最大过滤 size 沿着给定的轴线。

  • 这个 minimum_filter 函数计算多维最小过滤。必须提供矩形内核的大小或内核的占用空间。这个 size 参数(如果提供)必须是一系列大小或单个数字，在这种情况下，假定过滤沿每个轴的大小相等。这个 占地面积 如果提供，则必须是通过非零元素定义内核形状的数组。

  • 这个 maximum_filter 函数计算多维最大过滤。必须提供矩形内核的大小或内核的占用空间。这个 size 参数(如果提供)必须是一系列大小或单个数字，在这种情况下，假定过滤沿每个轴的大小相等。这个 占地面积 如果提供，则必须是通过非零元素定义内核形状的数组。

  • 这个 rank_filter 函数计算过滤的多维排名。这个 rank 可以小于零，即， rank =-1表示最大的元素。必须提供矩形内核的大小或内核的占用空间。这个 size 参数(如果提供)必须是一系列大小或单个数字，在这种情况下，假定过滤沿每个轴的大小相等。这个 占地面积 如果提供，则必须是通过非零元素定义内核形状的数组。

  • 这个 percentile_filter 函数计算多维百分位过滤。这个 百分位数 可以小于零，即， 百分位数 =-20等于 百分位数 =80。必须提供矩形内核的大小或内核的占用空间。这个 size 参数(如果提供)必须是一系列大小或单个数字，在这种情况下，假定过滤沿每个轴的大小相等。这个 占地面积 如果提供，则必须是通过非零元素定义内核形状的数组。

  • 这个 median_filter 函数计算多维中位数过滤。必须提供矩形内核的大小或内核的占用空间。这个 size 参数(如果提供)必须是一系列大小或单个数字，在这种情况下，假定过滤沿每个轴的大小相等。这个 占地面积 如果提供，则必须是通过非零元素定义内核形状的数组。

衍生品

可以用几种方式构造导数滤波器。该函数 gaussian_filter1d ，请参阅 平滑过滤器 属性计算沿给定轴的导数。 订单 参数。其他派生过滤器有Prewitt和Sobel过滤器：

  • 这个 prewitt 函数计算沿给定轴的导数。

  • 这个 sobel 函数计算沿给定轴的导数。

拉普拉斯过滤是由所有轴上的二阶导数之和计算出来的。因此，可以使用不同的二阶导数函数来构造不同的拉普拉斯滤波器。因此，我们提供了一个带有函数自变量的通用函数来计算沿给定方向的二阶导数。

  • 该函数 generic_laplace 使用传递的函数计算拉普拉斯过滤 derivative2 来计算二阶导数。该函数 derivative2 应具有以下签名

    derivative2(input, axis, output, mode, cval, *extra_arguments, **extra_keywords)

    它应该计算沿维度的二阶导数 axis 。如果 输出 不是 None ，它应该将其用于输出和返回 None ，否则它应该返回结果。 mode ， cval 有通常的意思。

    这个 extra_arguments 和 extra_keywords 参数可用于传递额外参数的元组和命名参数的字典，这些参数将传递给 derivative2 在每次呼叫时。

    例如

    >>> def d2(input, axis, output, mode, cval):
...     return correlate1d(input, [1, -2, 1], axis, output, mode, cval, 0)
...
>>> a = np.zeros((5, 5))
>>> a[2, 2] = 1
>>> from scipy.ndimage import generic_laplace
>>> generic_laplace(a, d2)
array([[ 0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  0.,  0.],
       [ 0.,  1., -4.,  1.,  0.],
       [ 0.,  0.,  1.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.]])

    要演示如何使用 extra_arguments 争论，我们可以这样做

    >>> def d2(input, axis, output, mode, cval, weights):
...     return correlate1d(input, weights, axis, output, mode, cval, 0,)
...
>>> a = np.zeros((5, 5))
>>> a[2, 2] = 1
>>> generic_laplace(a, d2, extra_arguments = ([1, -2, 1],))
array([[ 0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  0.,  0.],
       [ 0.,  1., -4.,  1.,  0.],
       [ 0.,  0.,  1.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.]])

    或

    >>> generic_laplace(a, d2, extra_keywords = {'weights': [1, -2, 1]})
array([[ 0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  0.,  0.],
       [ 0.,  1., -4.,  1.,  0.],
       [ 0.,  0.,  1.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.]])

以下两个函数使用 generic_laplace 通过为二阶导数函数提供适当的函数：

  • 该函数 laplace 使用二阶导数的离散微分计算拉普拉斯(即，与 [1, -2, 1] )。

  • 该函数 gaussian_laplace 使用以下公式计算拉普拉斯过滤 gaussian_filter 来计算二阶导数。高斯过滤沿每个轴的标准差通过参数传递 西格玛 作为序列或数字。如果 西格玛 不是序列而是单个数字，过滤的标准差在各个方向都是相等的。

梯度大小定义为所有方向上梯度平方和的平方根。与泛型Laplace函数类似，有一个 generic_gradient_magnitude 计算数组的梯度大小的函数。

  • 该函数 generic_gradient_magnitude 使用传递的函数计算渐变幅度 derivative 来计算一阶导数。该函数 derivative 应具有以下签名

    derivative(input, axis, output, mode, cval, *extra_arguments, **extra_keywords)

    它应该计算沿维度的导数 axis 。如果 输出 不是 None ，它应该将其用于输出和返回 None ，否则它应该返回结果。 mode ， cval 有通常的意思。

    这个 extra_arguments 和 extra_keywords 参数可用于传递额外参数的元组和命名参数的字典，这些参数将传递给 导数 在每次呼叫时。

    例如， sobel 函数符合所需的签名

    >>> a = np.zeros((5, 5))
>>> a[2, 2] = 1
>>> from scipy.ndimage import sobel, generic_gradient_magnitude
>>> generic_gradient_magnitude(a, sobel)
array([[ 0.        ,  0.        ,  0.        ,  0.        ,  0.        ],
       [ 0.        ,  1.41421356,  2.        ,  1.41421356,  0.        ],
       [ 0.        ,  2.        ,  0.        ,  2.        ,  0.        ],
       [ 0.        ,  1.41421356,  2.        ,  1.41421356,  0.        ],
       [ 0.        ,  0.        ,  0.        ,  0.        ,  0.        ]])

    请参阅的文档 generic_laplace 有关使用 extra_arguments 和 extra_keywords 争论。

这个 sobel 和 prewitt 函数符合所需的签名，因此可以直接用于 generic_gradient_magnitude 。

  • 该函数 gaussian_gradient_magnitude 使用以下参数计算渐变幅度 gaussian_filter 来计算一阶导数。高斯过滤沿每个轴的标准差通过参数传递 西格玛 作为序列或数字。如果 西格玛 不是序列而是单个数字，过滤的标准差在各个方向都是相等的。

通用过滤函数

要实现过滤函数，可以使用接受实现过滤操作的可调用对象的泛型函数。输入和输出数组上的迭代由这些泛型函数处理，以及边界条件的实现等细节。必须只提供实现执行实际过滤工作的回调函数的可调用对象。回调函数也可以用C语言编写，并使用 PyCapsule (请参阅 扩展 scipy.ndimage 在C中 了解更多信息)。

  • 这个 generic_filter1d 函数实现一般的一维过滤函数，其中实际的过滤操作必须作为Python函数(或其他可调用对象)提供。这个 generic_filter1d 函数遍历数组的各行并调用 function 在每一行。传递给 function 是一维的数组，这些数组是 numpy.float64 键入。第一个包含当前行的值。它是在开始和结束时扩展的，根据 filter_size 和 原点 争论。应就地修改第二个数组，以提供该行的输出值。例如，考虑沿一个维度的关联：

    >>> a = np.arange(12).reshape(3,4)
>>> correlate1d(a, [1, 2, 3])
array([[ 3,  8, 14, 17],
       [27, 32, 38, 41],
       [51, 56, 62, 65]])

    可以使用以下命令实现相同的操作 generic_filter1d ，详情如下：

    >>> def fnc(iline, oline):
...     oline[...] = iline[:-2] + 2 * iline[1:-1] + 3 * iline[2:]
...
>>> from scipy.ndimage import generic_filter1d
>>> generic_filter1d(a, fnc, 3)
array([[ 3,  8, 14, 17],
       [27, 32, 38, 41],
       [51, 56, 62, 65]])

    在这里，内核的原点(默认情况下)假设在长度为3的过滤的中间。因此，在调用函数之前，每一个输入行在开始和结束时都扩展了一个值。

    或者，可以定义额外的参数并将其传递给过滤函数。这个 extra_arguments 和 extra_keywords 参数可用于传递额外参数的元组和/或命名参数的字典，这些参数将在每次调用时传递给派生函数。例如，我们可以将过滤的参数作为参数传递

    >>> def fnc(iline, oline, a, b):
...     oline[...] = iline[:-2] + a * iline[1:-1] + b * iline[2:]
...
>>> generic_filter1d(a, fnc, 3, extra_arguments = (2, 3))
array([[ 3,  8, 14, 17],
       [27, 32, 38, 41],
       [51, 56, 62, 65]])

    或

    >>> generic_filter1d(a, fnc, 3, extra_keywords = {'a':2, 'b':3})
array([[ 3,  8, 14, 17],
       [27, 32, 38, 41],
       [51, 56, 62, 65]])

  • 这个 generic_filter 函数实现一个通用的过滤函数，其中实际的过滤操作必须作为Python函数(或其他可调用对象)提供。这个 generic_filter 函数迭代数组并调用 function 在每个元素上。的论据 function 是一个一维的数组，该数组包含 numpy.float64 包含过滤足迹内当前元素周围的值的类型。该函数应返回可转换为双精度数字的单个值。例如，考虑一种相关性：

    >>> a = np.arange(12).reshape(3,4)
>>> correlate(a, [[1, 0], [0, 3]])
array([[ 0,  3,  7, 11],
       [12, 15, 19, 23],
       [28, 31, 35, 39]])

    可以使用以下命令实现相同的操作 generic_filter ，详情如下：

    >>> def fnc(buffer):
...     return (buffer * np.array([1, 3])).sum()
...
>>> from scipy.ndimage import generic_filter
>>> generic_filter(a, fnc, footprint = [[1, 0], [0, 1]])
array([[ 0,  3,  7, 11],
       [12, 15, 19, 23],
       [28, 31, 35, 39]])

    在这里，指定了只包含两个元素的内核占用空间。因此，过滤函数接收长度等于2的缓冲区，该缓冲区与适当的权重相乘并将结果相加。

    当呼叫时 generic_filter ，则必须提供矩形内核的大小或内核的占用空间。这个 size 参数(如果提供)必须是一系列大小或单个数字，在这种情况下，假定过滤沿每个轴的大小相等。这个 占地面积 如果提供，则必须是通过非零元素定义内核形状的数组。

    或者，可以定义额外的参数并将其传递给过滤函数。这个 extra_arguments 和 extra_keywords 参数可用于传递额外参数的元组和/或命名参数的字典，这些参数将在每次调用时传递给派生函数。例如，我们可以将过滤的参数作为参数传递

    >>> def fnc(buffer, weights):
...     weights = np.asarray(weights)
...     return (buffer * weights).sum()
...
>>> generic_filter(a, fnc, footprint = [[1, 0], [0, 1]], extra_arguments = ([1, 3],))
array([[ 0,  3,  7, 11],
       [12, 15, 19, 23],
       [28, 31, 35, 39]])

    或

    >>> generic_filter(a, fnc, footprint = [[1, 0], [0, 1]], extra_keywords= {'weights': [1, 3]})
array([[ 0,  3,  7, 11],
       [12, 15, 19, 23],
       [28, 31, 35, 39]])

这些函数迭代从最后一个轴开始的行或元素，即最后一个索引更改最快。在根据空间位置调整过滤很重要的情况下，这种迭代顺序是有保证的。下面是一个使用实现过滤并在迭代时跟踪当前坐标的类的示例。它执行与上述相同的过滤操作 generic_filter ，但另外打印当前坐标：

>>> a = np.arange(12).reshape(3,4)
>>>
>>> class fnc_class:
...     def __init__(self, shape):
...         # store the shape:
...         self.shape = shape
...         # initialize the coordinates:
...         self.coordinates = [0] * len(shape)
...
...     def filter(self, buffer):
...         result = (buffer * np.array([1, 3])).sum()
...         print(self.coordinates)
...         # calculate the next coordinates:
...         axes = list(range(len(self.shape)))
...         axes.reverse()
...         for jj in axes:
...             if self.coordinates[jj] < self.shape[jj] - 1:
...                 self.coordinates[jj] += 1
...                 break
...             else:
...                 self.coordinates[jj] = 0
...         return result
...
>>> fnc = fnc_class(shape = (3,4))
>>> generic_filter(a, fnc.filter, footprint = [[1, 0], [0, 1]])
[0, 0]
[0, 1]
[0, 2]
[0, 3]
[1, 0]
[1, 1]
[1, 2]
[1, 3]
[2, 0]
[2, 1]
[2, 2]
[2, 3]
array([[ 0,  3,  7, 11],
       [12, 15, 19, 23],
       [28, 31, 35, 39]])

对于 generic_filter1d 函数时，除了此函数不会迭代正在筛选的轴之外，其他方法都是相同的。的示例 generic_filter1d 然后变成这样：

>>> a = np.arange(12).reshape(3,4)
>>>
>>> class fnc1d_class:
...     def __init__(self, shape, axis = -1):
...         # store the filter axis:
...         self.axis = axis
...         # store the shape:
...         self.shape = shape
...         # initialize the coordinates:
...         self.coordinates = [0] * len(shape)
...
...     def filter(self, iline, oline):
...         oline[...] = iline[:-2] + 2 * iline[1:-1] + 3 * iline[2:]
...         print(self.coordinates)
...         # calculate the next coordinates:
...         axes = list(range(len(self.shape)))
...         # skip the filter axis:
...         del axes[self.axis]
...         axes.reverse()
...         for jj in axes:
...             if self.coordinates[jj] < self.shape[jj] - 1:
...                 self.coordinates[jj] += 1
...                 break
...             else:
...                 self.coordinates[jj] = 0
...
>>> fnc = fnc1d_class(shape = (3,4))
>>> generic_filter1d(a, fnc.filter, 3)
[0, 0]
[1, 0]
[2, 0]
array([[ 3,  8, 14, 17],
       [27, 32, 38, 41],
       [51, 56, 62, 65]])

傅立叶域滤波器

本节中描述的函数在傅立叶域中执行滤波操作。因此，这种函数的输入数组应该与傅里叶逆变换函数兼容，例如来自 numpy.fft 模块。因此，我们必须处理可能是实数或复数傅立叶变换结果的数组。在实傅立叶变换的情况下，仅存储对称复数变换的一半。另外，需要知道通过真实FFT变换的轴的长度是多少。此处描述的函数提供了一个参数 n 在实数变换的情况下，必须等于变换前的实数变换轴的长度。如果该参数小于零，则假定输入阵列是复傅立叶变换的结果。该参数 axis 可用于指示沿哪个轴执行实际变换。

  • 这个 fourier_shift 函数将输入数组与给定移位的移位操作的多维傅立叶变换相乘。这个 换班 参数是每个维度的移位序列或所有维度的单个值。

  • 这个 fourier_gaussian 函数将输入阵列与具有给定标准差的高斯过滤的多维傅里叶变换相乘 西格玛 。这个 西格玛 参数是每个维度的一系列值或所有维度的单个值。

  • 这个 fourier_uniform 函数将输入数组与给定大小的均匀过滤的多维傅立叶变换相乘 size 。这个 size 参数是每个维度的一系列值或所有维度的单个值。

  • 这个 fourier_ellipsoid 函数将输入数组与给定大小的椭圆形过滤的多维傅立叶变换相乘 size 。这个 size 参数是每个维度的一系列值或所有维度的单个值。此函数仅在维度1、维度2和维度3中实现。

插值函数

本节介绍基于B样条理论的各种插值函数。有关B样条的详细介绍，请参阅 1 中给出了详细的图像插值算法 5.

样条预滤波器

使用大于1阶样条线的插值需要预过滤步骤。一节中介绍的插值函数 插值函数 通过调用 spline_filter ，但可以指示它们不要这样做，方法是将 预滤器 关键字等于False。如果在同一阵列上执行多个插值操作，则此选项非常有用。在这种情况下，只进行一次预滤波，并使用预滤波数组作为插值函数的输入，效率更高。以下两个函数实现预过滤：

  • 这个 spline_filter1d 函数沿给定轴计算一维样条线过滤。可以任选地提供输出阵列。样条曲线的阶数必须大于1且小于6。

  • 这个 spline_filter 函数计算多维样条线过滤。

    注解

    多维过滤由一系列一维样条线滤波器实现。中间数组以与输出相同的数据类型存储。因此，如果请求精度有限的输出，则结果可能不精确，因为中间结果的存储精度可能不够高。这可以通过指定高精度的输出类型来防止。

插值边界处理

插值函数都使用样条插值来实现输入阵列的某种类型的几何变换。这需要将输出坐标映射到输入坐标，因此，可能需要边界之外的输入值。此问题的解决方式与 过滤函数 对于多维的过滤功能。因此，这些函数都支持 mode 参数，该参数确定如何处理边界，以及一个 cval 在使用“Constant”模式时提供常量值的参数。所有模式的行为，包括在非整数位置的行为如下所示。请注意，所有模式的边界处理方式不尽相同； reflect (又名 grid-mirror )和 grid-wrap 涉及关于图像样本(虚线垂直线)中间的点的对称或重复，而模式 mirror 和 wrap 将图像视为其范围恰好在第一个和最后一个采样点结束，而不是超过它的0.5个采样。

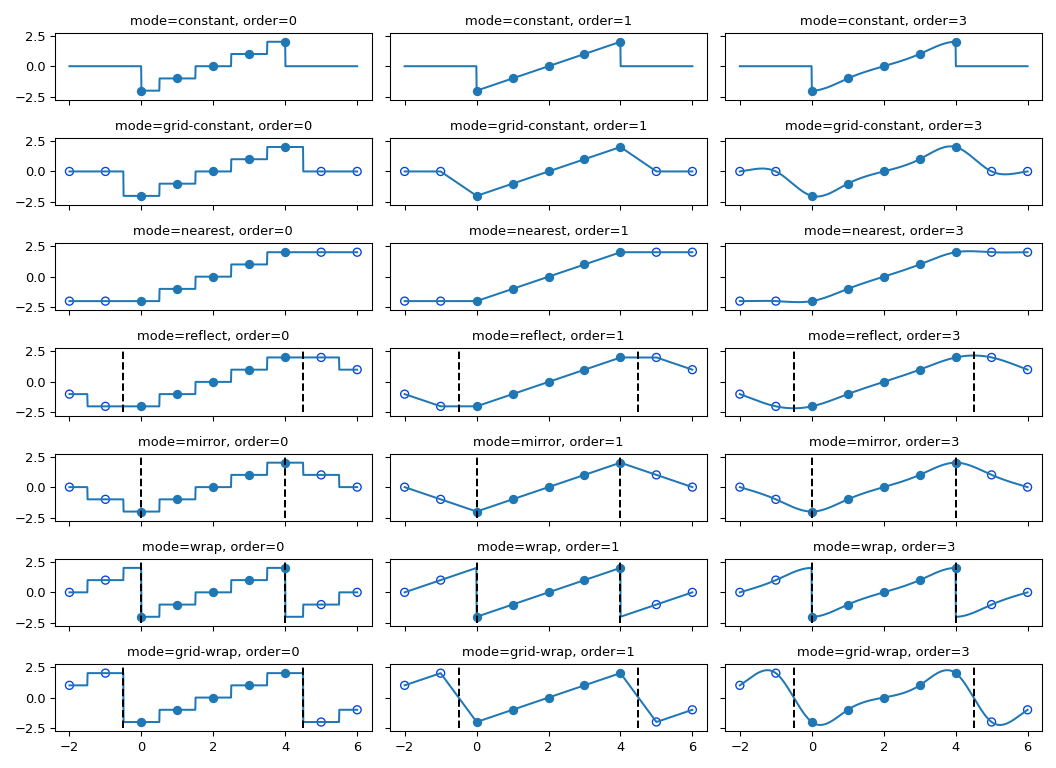
../_images/plot_boundary_modes.png

图像样本的坐标落在0到范围内的整数采样位置 shape[i] - 1 沿着每个轴， i 。下图说明了某个点在位置处的插值 (3.7, 3.3) 在形状的图像中 (7, 7) 。对于阶次插值 n ， n + 1 每个轴上都涉及到样本。实心圆圈说明了红色x位置处的值内插所涉及的采样位置。

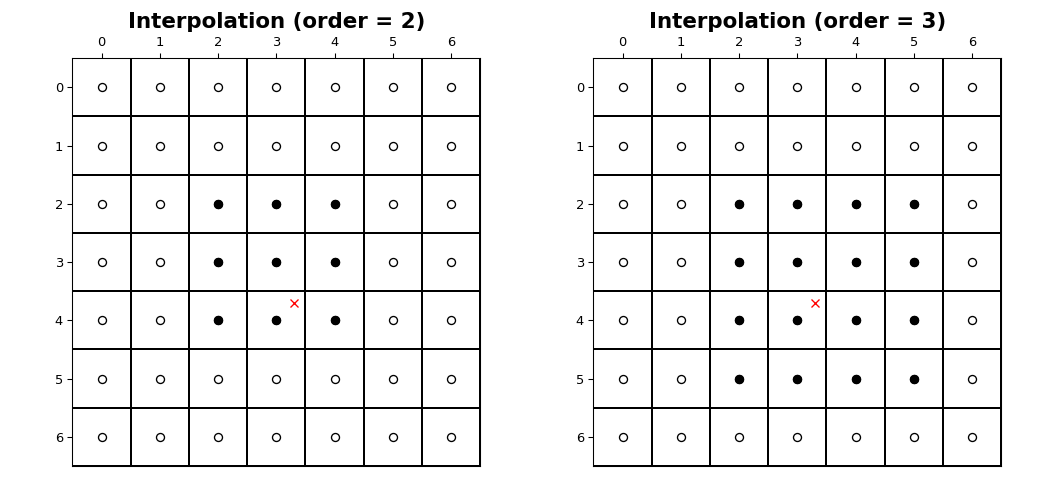
../_images/plot_interp_grid.png

插值函数

  • 这个 geometric_transform 函数对输入应用任意几何变换。给定的 映射 函数在输出中的每个点被调用，以查找输入中的相应坐标。 映射 必须是接受等于输出数组秩的长度元组并将相应的输入坐标作为等于输入数组秩的长度元组返回的可调用对象。可以任选地提供输出形状和输出类型。如果未指定，则它们等于输入形状和类型。

    例如：

    >>> a = np.arange(12).reshape(4,3).astype(np.float64)
>>> def shift_func(output_coordinates):
...     return (output_coordinates[0] - 0.5, output_coordinates[1] - 0.5)
...
>>> from scipy.ndimage import geometric_transform
>>> geometric_transform(a, shift_func)
array([[ 0.    ,  0.    ,  0.    ],
       [ 0.    ,  1.3625,  2.7375],
       [ 0.    ,  4.8125,  6.1875],
       [ 0.    ,  8.2625,  9.6375]])

    或者，可以定义额外的参数并将其传递给过滤函数。这个 extra_arguments 和 extra_keywords 参数可用于传递额外参数的元组和/或命名参数的字典，这些参数将在每次调用时传递给派生函数。例如，我们可以将示例中的移位作为参数传递

    >>> def shift_func(output_coordinates, s0, s1):
...     return (output_coordinates[0] - s0, output_coordinates[1] - s1)
...
>>> geometric_transform(a, shift_func, extra_arguments = (0.5, 0.5))
array([[ 0.    ,  0.    ,  0.    ],
       [ 0.    ,  1.3625,  2.7375],
       [ 0.    ,  4.8125,  6.1875],
       [ 0.    ,  8.2625,  9.6375]])

    或

    >>> geometric_transform(a, shift_func, extra_keywords = {'s0': 0.5, 's1': 0.5})
array([[ 0.    ,  0.    ,  0.    ],
       [ 0.    ,  1.3625,  2.7375],
       [ 0.    ,  4.8125,  6.1875],
       [ 0.    ,  8.2625,  9.6375]])

    注解

    映射函数也可以用C语言编写，并使用 scipy.LowLevelCallable 。看见 扩展 scipy.ndimage 在C中 了解更多信息。

  • 该函数 map_coordinates 使用给定的坐标数组应用任意坐标变换。输出的形状是通过放下第一个轴从坐标数组的形状派生出来的。该参数 坐标 用于为输出中的每个点查找输入中的相应坐标。的价值 坐标 沿着第一个轴的是输入数组中找到输出值的坐标。(另请参阅数字数组 coordinates 功能。)由于坐标可以是非整数坐标，因此这些坐标处的输入值由所请求阶次的样条插值来确定。

    下面是一个将二维数组插值为 (0.5, 0.5) 和 (1, 2) ：

    >>> a = np.arange(12).reshape(4,3).astype(np.float64)
>>> a
array([[  0.,   1.,   2.],
       [  3.,   4.,   5.],
       [  6.,   7.,   8.],
       [  9.,  10.,  11.]])
>>> from scipy.ndimage import map_coordinates
>>> map_coordinates(a, [[0.5, 2], [0.5, 1]])
array([ 1.3625,  7.])

  • 这个 affine_transform 函数将仿射变换应用于输入数组。给定的变换 矩阵 和 偏移 用于为输出中的每个点查找输入中的相应坐标。计算坐标处的输入值由所请求阶次的样条插值确定。转型 矩阵 必须是二维的，或者也可以作为一维序列或数组给出。在后一种情况下，假定矩阵是对角线的。然后应用一种更有效的插值算法，该算法利用了问题的可分性。可以任选地提供输出形状和输出类型。如果未指定，则它们等于输入形状和类型。

  • 这个 shift 函数使用请求的样条插值返回输入的移位版本 订单 。

  • 这个 zoom 函数使用请求的样条插值返回输入的重新缩放版本 订单 。

  • 这个 rotate 函数返回在由参数给定的两个轴定义的平面内旋转的输入数组 axes ，使用请求的 订单 。角度必须以度为单位。如果 重塑 为真，则输出数组的大小适用于包含旋转后的输入。

形态学

二元形态学

  • 这个 generate_binary_structure 函数生成用于二进制形态运算的二进制结构元素。这个 rank 必须提供该结构的。返回的结构的大小在每个方向上等于3。如果元素到中心的欧几里得距离的平方小于或等于，则每个元素的值等于1 连通性 。例如，2-D、4-连接和8-连接结构的生成如下所示：

    >>> from scipy.ndimage import generate_binary_structure
>>> generate_binary_structure(2, 1)
array([[False,  True, False],
       [ True,  True,  True],
       [False,  True, False]], dtype=bool)
>>> generate_binary_structure(2, 2)
array([[ True,  True,  True],
       [ True,  True,  True],
       [ True,  True,  True]], dtype=bool)

大多数二元形态函数都可以用基本运算、侵蚀和膨胀来表示。

  • 这个 binary_erosion 函数实现具有给定结构元素的任意秩数组的二进制侵蚀。Origin参数控制结构元素的位置，如中所述 过滤函数 。如果未提供结构化元素，则使用生成连通性等于1的元素 generate_binary_structure 。这个 border_value 参数提供边界外数组的值。侵蚀会反复发生 迭代次数 泰晤士报。如果 迭代次数 小于1，则重复侵蚀，直到结果不再改变。如果一个 mask 数组，则在每次迭代中只修改在相应掩码元素处具有TRUE值的那些元素。

  • 这个 binary_dilation 函数实现具有给定结构元素的任意秩数组的二进制扩张。Origin参数控制结构元素的位置，如中所述 过滤函数 。如果未提供结构化元素，则使用生成连通性等于1的元素 generate_binary_structure 。这个 border_value 参数提供边界外数组的值。扩张是重复进行的 迭代次数 泰晤士报。如果 迭代次数 小于1，则重复膨胀，直到结果不再改变。如果一个 mask 数组，则在每次迭代中只修改在相应掩码元素处具有TRUE值的那些元素。

下面是一个使用 binary_dilation 要查找所有接触边界的元素，请使用数据数组作为掩码从边界重复展开空数组：

>>> struct = np.array([[0, 1, 0], [1, 1, 1], [0, 1, 0]])
>>> a = np.array([[1,0,0,0,0], [1,1,0,1,0], [0,0,1,1,0], [0,0,0,0,0]])
>>> a
array([[1, 0, 0, 0, 0],
       [1, 1, 0, 1, 0],
       [0, 0, 1, 1, 0],
       [0, 0, 0, 0, 0]])
>>> from scipy.ndimage import binary_dilation
>>> binary_dilation(np.zeros(a.shape), struct, -1, a, border_value=1)
array([[ True, False, False, False, False],
       [ True,  True, False, False, False],
       [False, False, False, False, False],
       [False, False, False, False, False]], dtype=bool)

这个 binary_erosion 和 binary_dilation 两个函数都有一个 迭代次数 参数，该参数允许多次重复侵蚀或膨胀。用给定的结构重复侵蚀或膨胀 n 时间相当于结构的侵蚀或膨胀， n-1 时代在自我膨胀。提供了一个函数，该函数允许对自身膨胀多次的结构进行计算：

  • 这个 iterate_structure 函数通过扩展输入结构返回结构 迭代 -1次自带。

    例如：

    >>> struct = generate_binary_structure(2, 1)
>>> struct
array([[False,  True, False],
       [ True,  True,  True],
       [False,  True, False]], dtype=bool)
>>> from scipy.ndimage import iterate_structure
>>> iterate_structure(struct, 2)
array([[False, False,  True, False, False],
       [False,  True,  True,  True, False],
       [ True,  True,  True,  True,  True],
       [False,  True,  True,  True, False],
       [False, False,  True, False, False]], dtype=bool)

If the origin of the original structure is equal to 0, then it is
also equal to 0 for the iterated structure. If not, the origin
must also be adapted if the equivalent of the *iterations*
erosions or dilations must be achieved with the iterated
structure. The adapted origin is simply obtained by multiplying
with the number of iterations. For convenience, the
:func:`iterate_structure` also returns the adapted origin if the
*origin* parameter is not ``None``:

.. code:: python

   >>> iterate_structure(struct, 2, -1)
   (array([[False, False,  True, False, False],
           [False,  True,  True,  True, False],
           [ True,  True,  True,  True,  True],
           [False,  True,  True,  True, False],
           [False, False,  True, False, False]], dtype=bool), [-2, -2])

其他形态学运算可以根据侵蚀和膨胀来定义。为方便起见，以下函数提供了其中一些操作：

  • 这个 binary_opening 函数实现具有给定结构元素的任意秩数组的二进制打开。二元打开相当于二元侵蚀，然后是具有相同结构元素的二元膨胀。Origin参数控制结构元素的位置，如中所述 过滤函数 。如果未提供结构化元素，则使用生成连通性等于1的元素 generate_binary_structure 。这个 迭代次数 参数给出执行的侵蚀次数，然后是相同的膨胀次数。

  • 这个 binary_closing 函数实现具有给定结构元素的任意秩数组的二进制关闭。二进制闭合相当于具有相同结构元素的二进制膨胀之后的二进制侵蚀。Origin参数控制结构元素的位置，如中所述 过滤函数 。如果未提供结构化元素，则使用生成连通性等于1的元素 generate_binary_structure 。这个 迭代次数 参数给出了在相同的侵蚀次数之后执行的膨胀次数。

  • 这个 binary_fill_holes 函数用于闭合二值图像中对象中的孔，其中该结构定义孔的连通性。Origin参数控制结构元素的位置，如中所述 过滤函数 。如果未提供结构化元素，则使用生成连通性等于1的元素 generate_binary_structure 。

  • 这个 binary_hit_or_miss 函数实现具有给定结构元素的任意秩数组的二进制命中或未命中转换。命中或未命中变换通过侵蚀具有第一结构的输入、侵蚀逻辑 not 第二个结构的输入，后跟逻辑 and 这两处侵蚀中。原点参数控制结构元素的位置，如中所述 过滤函数 。如果 起始点2 等于 None ，则将其设置为等于 起始点1 参数。如果没有提供第一结构元素，则使用以下方法生成具有等于1的连接性的结构元素 generate_binary_structure 。如果 结构2 未提供，则将其设置为等于逻辑 not 的 结构1 。

灰度形态学

灰度形态学运算等同于对具有任意值的数组进行运算的二进制形态学运算。下面，我们描述侵蚀、膨胀、打开和关闭的灰度等价物。这些操作的实现方式与中介绍的筛选器类似 过滤函数 ，我们参考本节来描述过滤内核和内存占用，以及数组边框的处理。灰度形态学操作可选地采用 结构 参数，该参数提供结构化元素的值。如果未给出此参数，则假定结构元素是平面的，其值等于零。结构的形状可以选择性地由 占地面积 参数。如果未给定此参数，则假定结构为矩形，其大小等于 结构 数组，或按 size 参数if 结构 是不会被给予的。这个 size 参数仅在以下情况下使用 结构 和 占地面积 ，在这种情况下，假定结构元素是矩形和扁平的，其尺寸由 size 。这个 size 参数(如果提供)必须是大小序列或单个数字，在这种情况下，假定过滤沿每个轴的大小相等。这个 占地面积 参数(如果提供)必须是通过非零元素定义内核形状的数组。

与二进制侵蚀和膨胀类似，也有灰度侵蚀和膨胀的操作：

灰度级打开和关闭操作可以类似于它们的二进制对应操作来定义：

  • 这个 grey_opening 函数实现任意秩数组的灰度开运算。灰阶开口相当于灰阶的侵蚀，然后是灰阶的膨胀。

  • 这个 grey_closing 函数实现任意秩数组的灰度闭合。灰阶开口相当于灰阶膨胀，然后是灰阶侵蚀。

  • 这个 morphological_gradient 函数实现任意秩数组的灰度形态梯度。灰度形态梯度等于灰度膨胀和灰度侵蚀的差值。

  • 这个 morphological_laplace 函数实现任意秩数组的灰度形态拉普拉斯。灰度形态拉普拉斯等于灰度膨胀和灰度侵蚀之和减去输入的两倍。

  • 这个 white_tophat 函数实现任意秩数组的白色高帽过滤。白色顶帽等于输入和灰度级开口的差值。

  • 这个 black_tophat 函数实现任意秩数组的黑色高帽过滤。黑色顶帽等于灰度闭合和输入的差值。

距离变换

距离变换用于计算从对象的每个元素到背景的最小距离。以下函数实现三种不同距离度量的距离转换：欧几里得、城市挡路和棋盘距离。

  • 该函数 distance_transform_cdt 使用倒角类型算法计算输入的距离变换，方法是将每个对象元素(由大于零的值定义)替换为到背景的最短距离(所有非对象元素)。结构决定了完成的倒角类型。如果结构等于“cityblock”，则使用 generate_binary_structure 平方距离等于1。如果结构等于“棋盘”，则使用 generate_binary_structure 平方距离等于阵列的秩。这些选择对应着对城市挡路和棋盘距离指标在两个维度的常见解读。

    除了距离变换之外，还可以计算特征变换。在这种情况下，沿结果的第一个轴返回最接近的背景元素的索引。这个 return_distances ，以及 return_indices 标志可用于指示是否必须返回距离变换、要素变换或两者。

    这个 距离 和 指数 参数可用于提供必须具有正确大小和类型(两者)的可选输出数组 numpy.int32 )。中介绍了用于实现此函数的算法的基础知识 2.

  • 该函数 distance_transform_edt 通过将每个对象元素(由大于零的值定义)替换为到背景(所有非对象元素)的最短欧几里德距离，计算输入的精确欧几里德距离变换。

    除了距离变换之外，还可以计算特征变换。在这种情况下，沿结果的第一个轴返回最接近的背景元素的索引。这个 return_distances 和 return_indices 标志可用于指示是否必须返回距离变换、要素变换或两者。

    或者，沿每个轴的采样可以由 取样 参数，该参数应该是等于输入秩的长度序列，或者假设采样沿所有轴相等的单个数字。

    这个 距离 和 指数 参数可用于提供必须具有正确大小和类型的可选输出数组 (numpy.float64 和 numpy.int32 )。用于实现此功能的算法在 3.

  • 该函数 distance_transform_bf 通过将每个对象元素(由大于零的值定义)替换为到背景的最短距离(所有非对象元素)，使用强力算法计算输入的距离变换。度量必须是“欧几里得”、“城市街区”或“棋盘”之一。

    除了距离变换之外，还可以计算特征变换。在这种情况下，沿结果的第一个轴返回最接近的背景元素的索引。这个 return_distances 和 return_indices 标志可用于指示是否必须返回距离变换、要素变换或两者。

    或者，沿每个轴的采样可以由 取样 参数，该参数应该是等于输入秩的长度序列，或者假设采样沿所有轴相等的单个数字。此参数仅在欧几里得距离变换的情况下使用。

    这个 距离 和 指数 参数可用于提供必须具有正确大小和类型的可选输出数组 (numpy.float64 和 numpy.int32 )。

    注解

    该函数使用慢速暴力算法，该函数 distance_transform_cdt 可以用来更高效地计算城市挡路和棋盘距离的转换。该函数 distance_transform_edt 可以用来更有效地计算精确的欧几里德距离变换。

分段和标注

分割是将感兴趣的对象从背景中分离出来的过程。最简单的方法可能是强度阈值，这很容易用 numpy 功能：

>>> a = np.array([[1,2,2,1,1,0],
...               [0,2,3,1,2,0],
...               [1,1,1,3,3,2],
...               [1,1,1,1,2,1]])
>>> np.where(a > 1, 1, 0)
array([[0, 1, 1, 0, 0, 0],
       [0, 1, 1, 0, 1, 0],
       [0, 0, 0, 1, 1, 1],
       [0, 0, 0, 0, 1, 0]])

结果是一个二值图像，其中的各个对象仍然需要识别和标记。该函数 label 生成一个数组，其中为每个对象指定一个唯一的编号：

  • 这个 label 函数生成一个数组，其中输入中的对象用整数索引标记。它返回一个由对象标签数组和找到的对象数组成的元组，除非 输出 参数，在这种情况下只返回对象的数量。对象的连接性由结构化元素定义。例如，在2D中，使用4连接的结构元素可以提供：

    >>> a = np.array([[0,1,1,0,0,0],[0,1,1,0,1,0],[0,0,0,1,1,1],[0,0,0,0,1,0]])
>>> s = [[0, 1, 0], [1,1,1], [0,1,0]]
>>> from scipy.ndimage import label
>>> label(a, s)
(array([[0, 1, 1, 0, 0, 0],
        [0, 1, 1, 0, 2, 0],
        [0, 0, 0, 2, 2, 2],
        [0, 0, 0, 0, 2, 0]]), 2)

    这两个对象没有连接，因为我们无法放置结构元素，使其与两个对象重叠。但是，8连接的结构元素仅产生单个对象：

    >>> a = np.array([[0,1,1,0,0,0],[0,1,1,0,1,0],[0,0,0,1,1,1],[0,0,0,0,1,0]])
>>> s = [[1,1,1], [1,1,1], [1,1,1]]
>>> label(a, s)[0]
array([[0, 1, 1, 0, 0, 0],
       [0, 1, 1, 0, 1, 0],
       [0, 0, 0, 1, 1, 1],
       [0, 0, 0, 0, 1, 0]])

    如果未提供结构化元素，则通过调用 generate_binary_structure (请参阅 二元形态学 )使用1的连接性(其在2D中是第一示例的4连接结构)。输入可以是任何类型，任何不等于零的值都被视为对象的一部分。如果需要重新标记对象索引数组(例如，在删除不需要的对象之后)，这将非常有用。只需将Label函数再次应用于索引数组。例如：

    >>> l, n = label([1, 0, 1, 0, 1])
>>> l
array([1, 0, 2, 0, 3])
>>> l = np.where(l != 2, l, 0)
>>> l
array([1, 0, 0, 0, 3])
>>> label(l)[0]
array([1, 0, 0, 0, 2])

    注解

    使用的结构元素 label 假设它是对称的。

例如，根据可以通过导数滤波器获得的对象边界的估计，存在大量用于分割的其他方法。一种这样的方法是分水岭分割。该函数 watershed_ift 从定位对象边界的数组(例如，由渐变幅值过滤生成)生成一个数组，其中每个对象都分配有唯一的标签。它使用包含对象初始标记的数组：

  • 这个 watershed_ift 函数使用图像森林变换应用来自标记的分水岭算法，如中所述 4.

  • 此函数的输入是应用变换的数组，以及通过唯一标签指定对象的标记数组，其中任何非零值都是标记。例如：

    >>> input = np.array([[0, 0, 0, 0, 0, 0, 0],
...                   [0, 1, 1, 1, 1, 1, 0],
...                   [0, 1, 0, 0, 0, 1, 0],
...                   [0, 1, 0, 0, 0, 1, 0],
...                   [0, 1, 0, 0, 0, 1, 0],
...                   [0, 1, 1, 1, 1, 1, 0],
...                   [0, 0, 0, 0, 0, 0, 0]], np.uint8)
>>> markers = np.array([[1, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 2, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0]], np.int8)
>>> from scipy.ndimage import watershed_ift
>>> watershed_ift(input, markers)
array([[1, 1, 1, 1, 1, 1, 1],
       [1, 1, 2, 2, 2, 1, 1],
       [1, 2, 2, 2, 2, 2, 1],
       [1, 2, 2, 2, 2, 2, 1],
       [1, 2, 2, 2, 2, 2, 1],
       [1, 1, 2, 2, 2, 1, 1],
       [1, 1, 1, 1, 1, 1, 1]], dtype=int8)

    这里，使用了两个标记来指定一个对象( 标记器 =2)和背景( 标记器 =1)。处理这些内容的顺序是任意的：将背景标记移动到数组的右下角会产生不同的结果：

    >>> markers = np.array([[0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 2, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 1]], np.int8)
>>> watershed_ift(input, markers)
array([[1, 1, 1, 1, 1, 1, 1],
       [1, 1, 1, 1, 1, 1, 1],
       [1, 1, 2, 2, 2, 1, 1],
       [1, 1, 2, 2, 2, 1, 1],
       [1, 1, 2, 2, 2, 1, 1],
       [1, 1, 1, 1, 1, 1, 1],
       [1, 1, 1, 1, 1, 1, 1]], dtype=int8)

    结果是对象( 标记器 =2)较小，因为第二个标记较早处理。如果假设第一个标记指定背景对象，则这可能不是期望的效果。所以呢， watershed_ift 将具有负值的标记显式视为背景标记，并在正常标记之后处理它们。例如，用负标记替换第一个标记会产生类似于第一个示例的结果：

    >>> markers = np.array([[0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 2, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, -1]], np.int8)
>>> watershed_ift(input, markers)
array([[-1, -1, -1, -1, -1, -1, -1],
       [-1, -1,  2,  2,  2, -1, -1],
       [-1,  2,  2,  2,  2,  2, -1],
       [-1,  2,  2,  2,  2,  2, -1],
       [-1,  2,  2,  2,  2,  2, -1],
       [-1, -1,  2,  2,  2, -1, -1],
       [-1, -1, -1, -1, -1, -1, -1]], dtype=int8)

    对象的连接性由结构化元素定义。如果未提供结构化元素，则通过调用 generate_binary_structure (请参阅 二元形态学 )使用1的连接性(在2D中是4连接的结构。)例如，在最后一个示例中使用8连接结构会产生不同的对象：

    >>> watershed_ift(input, markers,
...               structure = [[1,1,1], [1,1,1], [1,1,1]])
array([[-1, -1, -1, -1, -1, -1, -1],
       [-1,  2,  2,  2,  2,  2, -1],
       [-1,  2,  2,  2,  2,  2, -1],
       [-1,  2,  2,  2,  2,  2, -1],
       [-1,  2,  2,  2,  2,  2, -1],
       [-1,  2,  2,  2,  2,  2, -1],
       [-1, -1, -1, -1, -1, -1, -1]], dtype=int8)

    注解

    该计划的实施 watershed_ift 将输入的数据类型限制为 numpy.uint8 和 numpy.uint16 。

物体测量

给定标记对象的阵列，可以测量各个对象的属性。这个 find_objects 函数可用于生成切片列表，该列表为每个对象提供完全包含该对象的最小子数组：

  • 这个 find_objects 函数查找带标签的数组中的所有对象，并返回与包含该对象的数组中最小区域对应的切片列表。

    例如：

    >>> a = np.array([[0,1,1,0,0,0],[0,1,1,0,1,0],[0,0,0,1,1,1],[0,0,0,0,1,0]])
>>> l, n = label(a)
>>> from scipy.ndimage import find_objects
>>> f = find_objects(l)
>>> a[f[0]]
array([[1, 1],
       [1, 1]])
>>> a[f[1]]
array([[0, 1, 0],
       [1, 1, 1],
       [0, 1, 0]])

    该函数 find_objects 返回所有对象的切片，除非 max_label 参数大于零，在这种情况下只有第一个 max_label 返回对象。如果 标签 数组， None 是返回而不是切片。例如：

    >>> from scipy.ndimage import find_objects
>>> find_objects([1, 0, 3, 4], max_label = 3)
[(slice(0, 1, None),), None, (slice(2, 3, None),)]

由生成的切片列表 find_objects 对于查找数组中对象的位置和尺寸很有用，但也可用于对各个对象执行测量。比方说，我们想要找出图像中一个物体的强度之和：

>>> image = np.arange(4 * 6).reshape(4, 6)
>>> mask = np.array([[0,1,1,0,0,0],[0,1,1,0,1,0],[0,0,0,1,1,1],[0,0,0,0,1,0]])
>>> labels = label(mask)[0]
>>> slices = find_objects(labels)

然后我们可以计算第二个对象中元素的总和：

>>> np.where(labels[slices[1]] == 2, image[slices[1]], 0).sum()
80

然而，这并不是特别有效，并且对于其他类型的测量也可能更加复杂。因此，定义了几个接受对象标签数组和待测量对象的索引的测量函数。例如，可以通过以下方式计算强度之和：

>>> from scipy.ndimage import sum as ndi_sum
>>> ndi_sum(image, labels, 2)
80

对于大数组和小对象，将数组分片后调用测量函数效率更高：

>>> ndi_sum(image[slices[1]], labels[slices[1]], 2)
80

或者，我们可以使用单个函数调用对多个标签进行测量，返回结果列表。例如，在我们的示例中，为了测量背景和第二个对象的值之和，我们给出了一个标签列表：

>>> ndi_sum(image, labels, [0, 2])
array([178.0, 80.0])

下面描述的测量函数都支持 索引 指示应测量哪些对象的参数。的默认值 索引 是 None 。这表明标签大于零的所有元素都应被视为单个对象并进行测量。因此，在这种情况下， 标签 数组被视为由大于零的元素定义的掩码。如果 索引 是一个数字或一系列数字，它给出被测量对象的标签。如果 索引 是序列，则返回结果列表。如果满足以下条件，则返回多个结果的函数将其结果作为元组返回 索引 是单个数字，或者在以下情况下作为列表的元组 索引 是一个序列。

  • 这个 sum 函数计算具有由给定的标签的对象的元素的总和 索引 ，使用 标签 对象标签的数组。如果 索引 是 None ，则将具有非零标签值的所有元素视为单个对象。如果 标签 是 None ，所有元素 输入 在计算中使用。

  • 这个 mean 函数使用由给定的标签计算对象元素的平均值 索引 ，使用 标签 对象标签的数组。如果 索引 是 None ，则将具有非零标签值的所有元素视为单个对象。如果 标签 是 None ，所有元素 输入 在计算中使用。

  • 这个 variance 函数计算具有由给定标签的对象的元素的方差 索引 ，使用 标签 对象标签的数组。如果 索引 是 None ，则将具有非零标签值的所有元素视为单个对象。如果 标签 是 None ，所有元素 输入 在计算中使用。

  • 这个 standard_deviation 函数计算具有由给出的标签的对象元素的标准差 索引 ，使用 标签 对象标签的数组。如果 索引 是 None ，则将具有非零标签值的所有元素视为单个对象。如果 标签 是 None ，所有元素 输入 在计算中使用。

  • 这个 minimum 函数计算具有由给定的标签的对象的最小元素 索引 ，使用 标签 对象标签的数组。如果 索引 是 None ，则将具有非零标签值的所有元素视为单个对象。如果 标签 是 None ，所有元素 输入 在计算中使用。

  • 这个 maximum 函数计算具有由给定的标签的对象的元素的最大值 索引 ，使用 标签 对象标签的数组。如果 索引 是 None ，则将具有非零标签值的所有元素视为单个对象。如果 标签 是 None ，所有元素 输入 在计算中使用。

  • 这个 minimum_position 函数计算具有由给定的标签的对象的最小元素的位置 索引 ，使用 标签 对象标签的数组。如果 索引 是 None ，则将具有非零标签值的所有元素视为单个对象。如果 标签 是 None ，所有元素 输入 在计算中使用。

  • 这个 maximum_position 函数计算具有由给定的标签的对象的元素的最大值的位置 索引 ，使用 标签 对象标签的数组。如果 索引 是 None ，则将具有非零标签值的所有元素视为单个对象。如果 标签 是 None ，所有元素 输入 在计算中使用。

  • 这个 extrema 函数计算具有由给定标签的对象的元素的最小值、最大值及其位置 索引 ，使用 标签 对象标签的数组。如果 索引 是 None ，则将具有非零标签值的所有元素视为单个对象。如果 标签 是 None ，所有元素 输入 在计算中使用。结果是一个元组，给出了最小值、最大值、最小值的位置和最大值的位置。结果与函数结果形成的元组相同 最低要求 ， 最大值 ， minimum_position ，以及 maximum_position 如上所述。

  • 这个 center_of_mass 函数使用由给定的标签计算对象的质心 索引 ，使用 标签 对象标签的数组。如果 索引 是 None ，则将具有非零标签值的所有元素视为单个对象。如果 标签 是 None ，所有元素 输入 在计算中使用。

  • 这个 histogram 函数计算具有由给定标签的对象的直方图 索引 ，使用 标签 对象标签的数组。如果 索引 是 None ，则将具有非零标签值的所有元素视为单个对象。如果 标签 是 None ，所有元素 输入 在计算中使用。直方图由其最小值定义( min )、最大( max )，以及垃圾桶数量( bins )。它们作为类型的一维数组返回 numpy.int32 。

扩展 scipy.ndimage 在C中

中的几个函数 scipy.ndimage 接受回调参数。它可以是python函数，也可以是 scipy.LowLevelCallable 包含指向C函数的指针的。使用C函数通常效率更高，因为它避免了在数组的许多元素上调用python函数的开销。要使用C函数，必须编写包含回调函数的C扩展和返回 scipy.LowLevelCallable 包含指向回调的指针的。

支持回调的函数示例如下 geometric_transform ，它接受一个回调函数，该函数定义从所有输出坐标到输入数组中相应坐标的映射。考虑下面的python示例，它使用 geometric_transform 来实现移位功能。

from scipy import ndimage

def transform(output_coordinates, shift):
    input_coordinates = output_coordinates[0] - shift, output_coordinates[1] - shift
    return input_coordinates

im = np.arange(12).reshape(4, 3).astype(np.float64)
shift = 0.5
print(ndimage.geometric_transform(im, transform, extra_arguments=(shift,)))

我们也可以用以下C代码实现回调函数：

/* example.c */

#include <Python.h>
#include <numpy/npy_common.h>

static int
_transform(npy_intp *output_coordinates, double *input_coordinates,
           int output_rank, int input_rank, void *user_data)
{
    npy_intp i;
    double shift = *(double *)user_data;

    for (i = 0; i < input_rank; i++) {
        input_coordinates[i] = output_coordinates[i] - shift;
    }
    return 1;
}

static char *transform_signature = "int (npy_intp *, double *, int, int, void *)";

static PyObject *
py_get_transform(PyObject *obj, PyObject *args)
{
    if (!PyArg_ParseTuple(args, "")) return NULL;
    return PyCapsule_New(_transform, transform_signature, NULL);
}

static PyMethodDef ExampleMethods[] = {
    {"get_transform", (PyCFunction)py_get_transform, METH_VARARGS, ""},
    {NULL, NULL, 0, NULL}
};

/* Initialize the module */
static struct PyModuleDef example = {
    PyModuleDef_HEAD_INIT,
    "example",
    NULL,
    -1,
    ExampleMethods,
    NULL,
    NULL,
    NULL,
    NULL
};

PyMODINIT_FUNC
PyInit_example(void)
{
    return PyModule_Create(&example);
}

有关编写Python扩展模块的详细信息，请参阅 `here`_ _。如果文件中有C代码 example.c ，则可以使用以下代码对其进行编译 setup.py ，

from distutils.core import setup, Extension
import numpy

shift = Extension('example',
                  ['example.c'],
                  include_dirs=[numpy.get_include()]
)

setup(name='example',
      ext_modules=[shift]
)

现在运行脚本

import ctypes
import numpy as np
from scipy import ndimage, LowLevelCallable

from example import get_transform

shift = 0.5

user_data = ctypes.c_double(shift)
ptr = ctypes.cast(ctypes.pointer(user_data), ctypes.c_void_p)
callback = LowLevelCallable(get_transform(), ptr)
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))

生成与原始Python脚本相同的结果。

在C版本中， _transform 是回调函数和参数 output_coordinates 和 input_coordinates 扮演与python版本中相同的角色，而 output_rank 和 input_rank 提供等价物 len(output_coordinates) 和 len(input_coordinates) 。变量 shift 是经过的 user_data 而不是 extra_arguments 。最后，C回调函数返回一个整数状态，成功时为1，否则为0。

该函数 py_transform 将回调函数包装在 PyCapsule 。主要步骤有：

  • 初始化为 PyCapsule 。第一个参数是指向回调函数的指针。

  • 第二个参数是函数签名，它必须与 ndimage 。

  • 在上面，我们使用 scipy.LowLevelCallable 要指定 user_data 我们用来生成的 ctypes 。

    另一种方法是在封装上下文中提供数据，可以通过 PyCapsule_SetContext 并省略指定 user_data 在……里面 scipy.LowLevelCallable 。然而，在这种方法中，我们需要处理数据的分配/释放-在销毁封装后释放数据可以通过在的第三个参数中指定一个非空的回调函数来完成 PyCapsule_New 。

C回调函数，用于 ndimage 所有人都遵循这个计划。下一节列出了 ndimage 接受C回调函数并给出函数原型的函数。

参见

支持低级回调参数的函数包括：

generic_filter, generic_filter1d, geometric_transform

下面，我们展示了编写代码的其他方法，使用 Numba, Cython, ctypes, 或 cffi 与其用C编写包装器代码，不如用C语言编写包装器代码。

Numba

Numba 提供了一种用Python轻松编写低级函数的方法。我们可以使用Numba将上述内容写成：

# example.py
import numpy as np
import ctypes
from scipy import ndimage, LowLevelCallable
from numba import cfunc, types, carray

@cfunc(types.intc(types.CPointer(types.intp),
                  types.CPointer(types.double),
                  types.intc,
                  types.intc,
                  types.voidptr))
def transform(output_coordinates_ptr, input_coordinates_ptr,
              output_rank, input_rank, user_data):
    input_coordinates = carray(input_coordinates_ptr, (input_rank,))
    output_coordinates = carray(output_coordinates_ptr, (output_rank,))
    shift = carray(user_data, (1,), types.double)[0]

    for i in range(input_rank):
        input_coordinates[i] = output_coordinates[i] - shift

    return 1

shift = 0.5

# Then call the function
user_data = ctypes.c_double(shift)
ptr = ctypes.cast(ctypes.pointer(user_data), ctypes.c_void_p)
callback = LowLevelCallable(transform.ctypes, ptr)

im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))

Cython

从功能上讲，可以用Cython编写与上面相同的代码，但使用的样板稍微少一些，如下所示：

# example.pyx

from numpy cimport npy_intp as intp

cdef api int transform(intp *output_coordinates, double *input_coordinates,
                       int output_rank, int input_rank, void *user_data):
    cdef intp i
    cdef double shift = (<double *>user_data)[0]

    for i in range(input_rank):
        input_coordinates[i] = output_coordinates[i] - shift
    return 1

# script.py

import ctypes
import numpy as np
from scipy import ndimage, LowLevelCallable

import example

shift = 0.5

user_data = ctypes.c_double(shift)
ptr = ctypes.cast(ctypes.pointer(user_data), ctypes.c_void_p)
callback = LowLevelCallable.from_cython(example, "transform", ptr)
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))

CFFI

使用 cffi, 您可以与驻留在共享库(DLL)中的C函数接口。首先，我们需要编写共享库，我们用C-这个示例是针对Linux/OSX的：

/*
  example.c
  Needs to be compiled with "gcc -std=c99 -shared -fPIC -o example.so example.c"
  or similar
 */

#include <stdint.h>

int
_transform(intptr_t *output_coordinates, double *input_coordinates,
           int output_rank, int input_rank, void *user_data)
{
    int i;
    double shift = *(double *)user_data;

    for (i = 0; i < input_rank; i++) {
        input_coordinates[i] = output_coordinates[i] - shift;
    }
    return 1;
}

调用库的Python代码为：

import os
import numpy as np
from scipy import ndimage, LowLevelCallable
import cffi

# Construct the FFI object, and copypaste the function declaration
ffi = cffi.FFI()
ffi.cdef("""
int _transform(intptr_t *output_coordinates, double *input_coordinates,
               int output_rank, int input_rank, void *user_data);
""")

# Open library
lib = ffi.dlopen(os.path.abspath("example.so"))

# Do the function call
user_data = ffi.new('double *', 0.5)
callback = LowLevelCallable(lib._transform, user_data)
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))

您可以在 cffi 文档。

CTYPE

使用 CTYPE ，C代码和SO/DLL的编译与上面的CFFI相同。Python代码不同：

# script.py

import os
import ctypes
import numpy as np
from scipy import ndimage, LowLevelCallable

lib = ctypes.CDLL(os.path.abspath('example.so'))

shift = 0.5

user_data = ctypes.c_double(shift)
ptr = ctypes.cast(ctypes.pointer(user_data), ctypes.c_void_p)

# Ctypes has no built-in intptr type, so override the signature
# instead of trying to get it via ctypes
callback = LowLevelCallable(lib._transform, ptr,
    "int _transform(intptr_t *, double *, int, int, void *)")

# Perform the call
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))

您可以在 ctypes 文档。

参考文献

1

M.Unser，“样条：信号和图像处理的完美匹配”，IEEE Signal Processing Magazine，Vol.16，第6期，第22-38页，1999年11月。

2

G.Borgefors，<任意维度的距离变换>，“计算机视觉、图形学和图像处理”，27：321-345,1984。

3

C.R.Maurer，Jr.，R.Qi和V.Raghavan，“一种用于计算任意维度的二值图像的精确欧几里德距离变换的线性时间算法”。IEEE传输帕米25,265-270,2003。

4

题名/责任者：Required，and，and，//R.X.Falcão，J.Stolfi，R.A.Lotufo。图像森林变换：理论、算法和应用。IEEE传输帕米26，19-29。2004年。

5

T.Briand和P.Monasse，“图像B样条插值的理论与实践”，“在线图像处理”，第8页，第99-141页，2018年。https://doi.org/10.5201/ipol.2018.221

上一页

朴素制服比(NROU)法

下一页

文件IO (scipy.io )