特殊功能 (scipy.special )

的主要功能是 scipy.special 包是数学物理众多特殊函数的定义。可用功能包括AIREY、椭圆、贝塞尔、伽马、贝塞尔、超几何、抛物线柱面、马蒂厄、椭球波、Struve和开尔文。还有一些低级统计信息函数不适合一般使用，因为这些函数的更简单接口由 stats module. Most of these functions can take array arguments and return array results following the same broadcasting rules as other math functions in Numerical Python. Many of these functions also accept complex numbers as input. For a complete list of the available functions with a one-line description type >>> help(special). 每个函数还具有自己的文档，可以使用帮助进行访问。如果您没有看到所需的函数，请考虑编写它并将其贡献给库。您可以用C、Fortran或Python编写函数。请查看该库的源代码，以获取每种类型函数的示例。

实数阶Bessel函数 (jv ， jn_zeros )

贝塞尔函数是实数或复数阶α的贝塞尔微分方程的一族解：

\[x^2\frac{d^2y}{dx^2}+x\frac{dy}{dx}+(x^2-\alpha^2)y=0\]

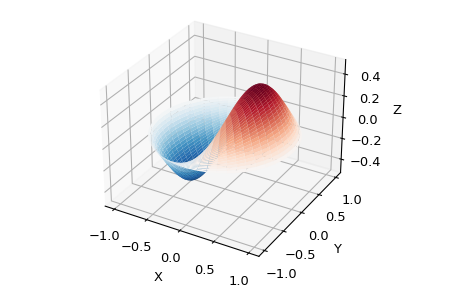
在其他用途中，这些函数出现在波传播问题中，例如薄鼓头的振动模式。以下是锚定在边缘的圆形鼓头的示例：

>>> from scipy import special
>>> def drumhead_height(n, k, distance, angle, t):
...    kth_zero = special.jn_zeros(n, k)[-1]
...    return np.cos(t) * np.cos(n*angle) * special.jn(n, distance*kth_zero)
>>> theta = np.r_[0:2*np.pi:50j]
>>> radius = np.r_[0:1:50j]
>>> x = np.array([r * np.cos(theta) for r in radius])
>>> y = np.array([r * np.sin(theta) for r in radius])
>>> z = np.array([drumhead_height(1, 1, r, theta, 0.5) for r in radius])

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_axes(rect=(0, 0.05, 0.95, 0.95), projection='3d')
>>> ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap='RdBu_r', vmin=-0.5, vmax=0.5)
>>> ax.set_xlabel('X')
>>> ax.set_ylabel('Y')
>>> ax.set_xticks(np.arange(-1, 1.1, 0.5))
>>> ax.set_yticks(np.arange(-1, 1.1, 0.5))
>>> ax.set_zlabel('Z')
>>> plt.show()

特殊函数的Cython绑定 (scipy.special.cython_special )

SciPy还特别为许多函数的标量、类型化版本提供了Cython绑定。下面的Cython代码提供了一个如何使用这些函数的简单示例：

cimport scipy.special.cython_special as csc

cdef:
    double x = 1
    double complex z = 1 + 1j
    double si, ci, rgam
    double complex cgam

rgam = csc.gamma(x)
print(rgam)
cgam = csc.gamma(z)
print(cgam)
csc.sici(x, &si, &ci)
print(si, ci)

(请参阅 Cython documentation 获取有关编译Cython的帮助。)在该示例中，函数 csc.gamma 其工作原理与ufunc的对应物基本相同 gamma ，尽管它以C类型而不是NumPy数组作为参数。特别要注意的是，该函数被重载以支持实数和复数参数；在编译时选择正确的变量。该函数 csc.sici 工作方式与 sici ；对于我们可以编写的ufunc ai, bi = sici(x) ，而在Cython版本中，多个返回值作为指针传递。将其视为类似于使用输出数组调用ufunc可能会有所帮助： sici(x, out=(si, ci)) 。

使用Cython绑定有两个潜在优势：

• 它们避免了Python函数开销

• 它们不需要Python全局解释器锁(GIL)

以下各节将讨论如何利用这些优势潜在地加速您的代码，当然，您应该始终首先分析代码，以确保付出额外的努力是值得的。

避免Python函数开销

特别是对于ufunction，通过向量化，即通过将数组传递给函数来避免Python函数开销。通常，这种方法工作得很好，但有时调用循环内标量输入的特殊函数会更方便，例如，在实现您自己的ufunc时。在这种情况下，Python函数开销可能会很大。请考虑以下示例：

import scipy.special as sc
cimport scipy.special.cython_special as csc

def python_tight_loop():
    cdef:
        int n
        double x = 1

    for n in range(100):
        sc.jv(n, x)

def cython_tight_loop():
    cdef:
        int n
        double x = 1

    for n in range(100):
        csc.jv(n, x)

在一台计算机上 python_tight_loop 大约用了131微秒就跑完了 cython_tight_loop 运行时间约为18.2微秒。显然，此示例是人为设计的：只需调用 special.jv(np.arange(100), 1) 并以同样快的速度获得结果 cython_tight_loop 。关键是，如果Python函数开销在您的代码中变得非常重要，那么Cython绑定可能会很有用。

释放Gil

人们通常需要在多个点计算一个特殊函数，并且通常计算是微不足道的并行化的。由于Cython绑定不需要GIL，因此使用Cython的 prange 功能。例如，假设我们要计算Helmholtz方程的基本解：

\[\Delta_x G(x，y)+k^2G(x，y)=\Delta(x-y)，\]

哪里 \(k\) 是波数和波数 \(\delta\) 是狄拉克增量函数。众所周知，在二维中，唯一(辐射)解是

\[G(x，y)=\frac{i}{4}H_0^{(1)}(k|x-y|)，\]

哪里 \(H_0^{{(1)}}\) 是第一类Hankel函数，即函数 hankel1 。以下示例显示如何并行计算此函数：

from libc.math cimport fabs
cimport cython
from cython.parallel cimport prange

import numpy as np
import scipy.special as sc
cimport scipy.special.cython_special as csc

def serial_G(k, x, y):
    return 0.25j*sc.hankel1(0, k*np.abs(x - y))

@cython.boundscheck(False)
@cython.wraparound(False)
cdef void _parallel_G(double k, double[:,:] x, double[:,:] y,
                      double complex[:,:] out) nogil:
    cdef int i, j

    for i in prange(x.shape[0]):
        for j in range(y.shape[0]):
            out[i,j] = 0.25j*csc.hankel1(0, k*fabs(x[i,j] - y[i,j]))

def parallel_G(k, x, y):
    out = np.empty_like(x, dtype='complex128')
    _parallel_G(k, x, y, out)
    return out

(有关在Cython中编译并行代码的帮助，请参见 here 。)如果上面的Cython代码在文件中 test.pyx ，然后我们可以编写一个非正式基准来比较函数的并行和串行版本：

import timeit

import numpy as np

from test import serial_G, parallel_G

def main():
    k = 1
    x, y = np.linspace(-100, 100, 1000), np.linspace(-100, 100, 1000)
    x, y = np.meshgrid(x, y)

    def serial():
        serial_G(k, x, y)

    def parallel():
        parallel_G(k, x, y)

    time_serial = timeit.timeit(serial, number=3)
    time_parallel = timeit.timeit(parallel, number=3)
    print("Serial method took {:.3} seconds".format(time_serial))
    print("Parallel method took {:.3} seconds".format(time_parallel))

if __name__ == "__main__":
    main()

在一台四核计算机上，串行方法耗时1.29秒，并行方法耗时0.29秒。

不在中的函数 scipy.special

有些函数没有包含在SPECIAL中，因为使用NumPy和SciPy中的现有函数可以直接实现它们。为了避免重复发明轮子，本节提供了几个这样的函数的实现，希望能说明如何处理类似的函数。在所有示例中，NumPy都导入为 np 和SPECIAL被导入为 sc 。

这个 binary entropy function ：：

def binary_entropy(x):
    return -(sc.xlogy(x, x) + sc.xlog1py(1 - x, -x))/np.log(2)

上的矩形阶跃函数 [0, 1] ：：

def step(x):
    return 0.5*(np.sign(x) + np.sign(1 - x))

平移和缩放可用于获得任意阶跃函数。

这个 ramp function ：：

def ramp(x):
    return np.maximum(0, x)

上一页

引言

下一页

集成 (scipy.integrate )