朴素制服比(NROU)法

  • 要求：PDF

  • 可选：接受区域的模式、中心、边界矩形

  • 速度：

    • 设置：快速(如果边界矩形已知)，否则为慢

    • 采样：中等

NROU是使用(最小)边界矩形的(广义)均匀比方法的一种实现 (3, 5) 。它使用正控制参数r来将算法调整到给定分布，以提高性能和/或使该方法适用。较大的r值以较高的拒绝常数为代价增加了该方法适用的分布类别。出于计算原因，如果可能，应使用r=1。此外，此实现使用分布的中心。

如果 r==1 ，则该方法的工作方式如下：对于给定的pdf和常量 center ，定义集合 A = {{(u, v) : 0 < v <= sqrt(pdf(u/v + center))}} 。如果(U，V)是均匀分布在A上的随机向量，则 U/V + center 遵循根据pdf的分布。

典型的选择 center 是零还是PDF的模式。集合A是矩形的子集 R = [u_min, u_max] x [0, v_max] 哪里

  • v_max = sup_x sqrt(pdf(x))

  • u_min = inf_x (x - center) sqrt(pdf(x))

  • u_max = sup_x (x - center) sqrt(pdf(x))

特别地，如果pdf是有界的，并且这些值是有限的，则这些值是有限的 x**2 * pdf(x) 是有界的(即次二次尾部)。可以在R上均匀地生成(U，V)并返回 U/V + center 如果(U，V)也在A中，可以直接验证。

如果用与PDF成比例的函数替换PDF，例如通过丢弃不必要的归一化因子，则算法不会改变。

直观地说，如果A填满了包围矩形的大部分，使得当(U，V)位于R中时(U，V)位于A的概率很高，否则所需的迭代次数变得太大，则该方法效果很好。更精确地说，要在R上均匀地绘制(U，V)使得(U，V)也在A中的期望迭代次数由比率给出 area(R) / area(A) = 2 * v_max * (u_max - u_min) / area(pdf) ，在哪里 area(pdf) 是pdf的积分(如果使用概率密度函数，则其等于1，但是如果使用与密度成比例的函数，则可以采用其他值)。由于A的面积等于 0.5 * area(pdf) (定理7.1在 4) 。

在一般情况下，接受区域被定义为 A = {{(u, v) : 0 < v <= (pdf(u/v**r + center))**(1/(r+1))}} 边界矩形由

  • v_max = sup_x pdf(x)**(1/(r+1))

  • u_min = inf_x (x - center) (pdf(x))**(r/(r+1))

  • u_max = sup_x (x - center) (pdf(x))**(r/(r+1))

请注意，原始方法是一种特殊情况， r=1 。然后，采样按如下方式工作：

  • 生成 (U,V) 整齐划一地在 [u_min, u_max] x [0, v_max]

  • 设置 X = U/V**r + center

  • 如果 V**(r+1) <= pdf(X) ，返回 X

  • 否则，请重试

使用此方法的示例如下所示：

>>> import numpy as np
>>> from scipy.stats import NaiveRatioUniforms
>>>
>>> class StandardNormal:
...     def pdf(self, x):
...         # note that the normalization constant is not required
...         return np.exp(-0.5 * x*x)
>>> dist = StandardNormal()
>>> u_bound = np.sqrt(dist.pdf(np.sqrt(2))) * np.sqrt(2)
>>> urng = np.random.default_rng()
>>> rng = NaiveRatioUniforms(dist, v_max=1, u_min=-u_bound,
...                          u_max=u_bound, random_state=urng)
>>> rng.rvs()
-0.5677819961248616

在上面的例子中，我们使用了NROU方法从标准正态分布中进行抽样。请注意，我们在计算PDF时丢弃了归一化常量。这通常有助于加快采样阶段。另外，请注意PDF不需要矢量化。它应该接受并返回一个标量。

请注意， v_max 是由分配模式决定的。如果模式远离零，请注意 u_max 会变得很大，如果 center == 0 ：至少是这样 mode * pdf(mode)**(r/(r+1) 。这可以通过移动分布来避免，例如，如果 center == mode ，请参见 5. 我们用伽马分布来说明这一点。对于给定的形状参数 p > 0 ，密度与密度成正比 x**(p-1) * exp(-x) ：

>>> import math
>>>
>>> class Gamma:
...     def __init__(self, p):
...         self.p = p
...
...     def pdf(self, x):
...         if x < 0:
...             return 0.0
...         return x**(self.p - 1) * math.exp(-x)
...     @staticmethod
...     def support():
...         return 0, np.inf

如果 p < 1 ，pdf是无界的，我们不能使用NROU (v_max 需要是有限的)。如果 p >= 1`, the mode is at `` P-1。我们希望通过以下方式应用NROU r=1 。可以计算确定这些点的 u_min 和 u_max 通过找出以下函数的极值来明确表示：

>>> def u_bound(x, p, center):
...     if x < 0:
...         return 0
...     return (x - center) * x**((p-1)/2) * math.exp(-x/2)

取决于 p 和 center ，外接矩形由

>>> def rectangle(p, center):
...     h = (p+1+center)/2
...     k = np.sqrt(h**2 - center*(p-1))
...     u_min, u_max = u_bound(h-k, p, center), u_bound(h+k, p, center)
...     v_max = math.sqrt((p-1)**(p-1) * math.exp(-(p-1)))
...     return u_min, u_max, v_max

我们可以比较产生的拒绝常数，如果我们设置 center=0 和 center=p-1 (模式)对于不同的值 p 。我们使用上述拒绝常数的公式(请注意，我们需要考虑伽马密度的归一化常数)：

>>> from scipy import special as sc
>>> ps = np.arange(1.0, 2.5, 0.1)
>>> reject_const, reject_const_shift = [], []
>>> for p in ps:
...     # no shift (center=0)
...     u_min, u_max, v_max = rectangle(p, 0)
...     reject_const.append(2*v_max*(u_max - u_min) / sc.gamma(p))
...     # mode shift (center=p-1)
...     u_min, u_max, v_max = rectangle(p, p-1)
...     reject_const_shift.append(2*v_max*(u_max - u_min) / sc.gamma(p))

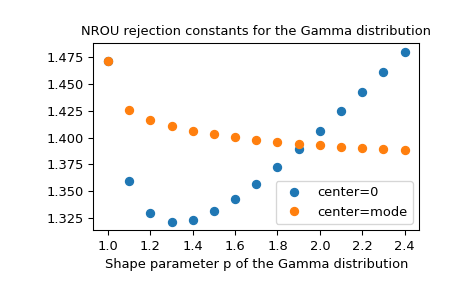
我们可以看到，随着模式进一步远离零，施加一次模式偏移是有利的：

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(ps, reject_const, 'o', label='center=0')
>>> ax.plot(ps, reject_const_shift, 'o', label='center=mode')
>>> plt.xlabel('Shape parameter p of the Gamma distribution')
>>> plt.title('NROU rejection constants for the Gamma distribution')
>>> plt.legend()
>>> plt.show()
../../_images/nrou_plot1.png

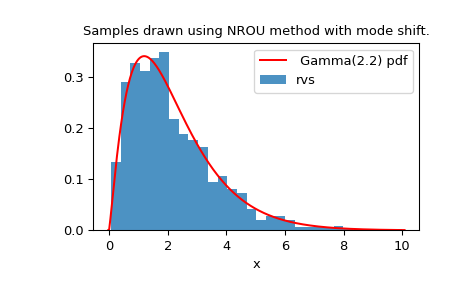
为结束此示例，我们为以下内容生成随机变量 Gamma(2.2) 通过将NROU与模式切换一起应用并创建直方图：

>>> from scipy import stats
>>> p = 2.2
>>> dist = Gamma(p)
>>> u_min, u_max, v_max = rectangle(p, p-1)
>>> rng = NaiveRatioUniforms(dist, center=p-1, v_max=v_max,
...                          u_min=u_min, u_max=u_max, random_state=urng)
>>> rvs = rng.rvs(1000)
>>> x = np.linspace(rvs.min()-0.1, rvs.max()+0.1, num=500)
>>> fx = stats.gamma.pdf(x, p)
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(x, fx, "r-", label=" Gamma({}) pdf".format(p))
>>> ax.hist(rvs, bins=30, density=True, alpha=0.8, label="rvs")
>>> plt.xlabel("x")
>>> plt.title("Samples drawn using NROU method with mode shift.")
>>> plt.legend()
>>> plt.show()
../../_images/nrou_plot2.png

最后，我们注意到该参数 r 可以用来转换密度。通常，建议使用 r=1 因为计算上的原因。但是，较大的r值会增加该方法适用的分布类别。例如，如果pdf的右尾减小为 x**(-1.5) ， u_max 如果满足以下条件，则不是有限的 r=1 因为 x*sqrt(x**(-1.5)) = x**(0.25) 是无界的，因为 x 增加。但是，如果我们使用 r=2 ，请注意 x * x**(-1.5*r/(r+1)) = 1 ，所以 u_max 是有界的。

请看 1, 2, 3, 4 和 5 有关此方法的更多详细信息，请参见。

参考文献

1

联合国参考手册，第5.3.11节，“朴素制服比法”，http://statmath.wu.ac.at/software/unuran/doc/unuran.html#NROU

2

书名/作者：Reinessy，and G.Derflinger(2004)，W.Hörmann，J.Leydold和G.非均匀随机变量自动生成，施普林格，柏林。

3(1,2)

A.J.Kinderman和J.F.Monahan，“使用均匀偏差比的随机变量的计算机生成”，数学软件学报，3(3)，第257-260页，1977。

4(1,2)

德德罗耶，“非均匀随机变量生成”，Springer-Verlag，1986。

5(1,2,3)

书名/作者声明：by J.C.韦克菲尔德、A.E.吉尔芬德和A.F.M.史密斯。“通过一致性比方法有效地生成随机变量。”“统计与计算”1.2，第129--133页，1991年。

上一页

基于多项式插值的CDF反演(PINV)

下一页

多维图像处理 (scipy.ndimage )