Lomb疤痕周期图

Lomb疤痕周期图（Lomb之后 [1], 还有疤痕 [2]) 是一种常用的统计工具，用于检测不均匀间隔观测中的周期性信号。这个 LombScargle 类是lombscargle周期图的几个实现的统一接口，包括 [O[n登录]] 按照Press&Rybicki提出的算法实现 [3].

这里的代码改编自 astroml 包裹 ([4], [5]) 以及 gatspy 包裹 ([6], [7]) . 对于Lomb抖动周期图的详细实际讨论，代码示例基于 astropy 见 Understanding the Lomb-Scargle Periodogram [11], 相关代码位于https://github.com/jakevdp/PracticalLombScargle/。

基本用法

备注

所有频率输入 LombScargle 是 not 角频率，而是振荡频率（即每单位时间的循环次数）。

Lomb Scargle周期图用于检测不均匀间隔观测中的周期信号。

例子

要在不均匀间隔观测中检测周期性信号，请考虑以下数据：

>>> import numpy as np
>>> rand = np.random.default_rng(42)
>>> t = 100 * rand.random(100)
>>> y = np.sin(2 * np.pi * t) + 0.1 * rand.standard_normal(100)

这些是在不规则时间进行的100次噪声测量，频率为每单位时间1个周期。

在根据输入数据自动选择的频率下评估的Lomb抖动周期图，可以使用 LombScargle 班级：

>>> from astropy.timeseries import LombScargle
>>> frequency, power = LombScargle(t, y).autopower()

使用Matplotlib绘制结果可以得到：

>>> import matplotlib.pyplot as plt  
>>> plt.plot(frequency, power)       

(png, svg, pdf)

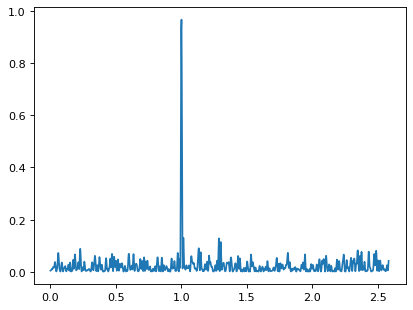
周期图显示了一个明显的峰值，频率为每单位时间1个周期，正如我们所构建的数据所预期的那样。

测量不确定度

这个 LombScargle 接口还可以处理具有测量不确定性的数据。

例子

如果所有不确定性都相同，则可以传递标量：

>>> dy = 0.1
>>> frequency, power = LombScargle(t, y, dy).autopower()

如果不确定性因观测而异，可以将其作为数组传递：

>>> dy = 0.1 * (1 + rand.random(100))
>>> y = np.sin(2 * np.pi * t) + dy * rand.standard_normal(100)
>>> frequency, power = LombScargle(t, y, dy).autopower()

假设高斯不确定性，以及 dy 这里指定标准差（不是方差）。

周期图和单位

这个 LombScargle 接口正确处理 Quantity 对象，并将验证输入以确保单位是适当的。

例子

使用 LombScargle 对于 Quantity 附着单位的对象：

>>> import astropy.units as u
>>> t_days = t * u.day
>>> y_mags = y * u.mag
>>> dy_mags = y * u.mag
>>> frequency, power = LombScargle(t_days, y_mags, dy_mags).autopower()
>>> frequency.unit
Unit("1 / d")
>>> power.unit
Unit(dimensionless)

我们看到输出是无量纲的，标准归一化周期图总是如此(有关归一化的更多信息，请参见 周期图规范化 (见下文)。如果您包含有关自动电源的参数，例如 minimum_frequency 或 maximum_frequency ，请确保同时指定单位：

>>> frequency, power = LombScargle(t_days, y_mags, dy_mags).autopower(minimum_frequency=1e-5*u.Hz)

指定频率

与 autopower() 采用上述方法，采用启发式方法选择合适的频率网格。默认情况下，启发式假设峰值宽度与观测基线成反比，最大频率比所谓的“平均奈奎斯特频率”大5倍，计算基于平均观测间隔。

这种启发式并非普遍有用，因为不规则采样数据探测到的频率可能远高于平均奈奎斯特频率。因此，可以通过传递给 autopower() 方法。

例子

使用传递给 autopower() 方法：

>>> frequency, power = LombScargle(t, y, dy).autopower(nyquist_factor=2)
>>> len(frequency), frequency.min(), frequency.max()  
(500, 0.0010327803641893758, 1.0317475838251864)

这里最高频率是平均奈奎斯特频率的两倍。如果我们增加 nyquist_factor ，我们可以探测更高频率：

>>> frequency, power = LombScargle(t, y, dy).autopower(nyquist_factor=10)
>>> len(frequency), frequency.min(), frequency.max()  
(2500, 0.0010327803641893758, 5.16286904058269)

或者，我们可以使用 power() 在用户指定的一组频率下评估周期图的方法：

>>> frequency = np.linspace(0.5, 1.5, 1000)
>>> power = LombScargle(t, y, dy).power(frequency)

请注意，最快的Lomb Scargle实现需要规则间隔的频率；如果频率间隔不规则，则将使用较慢的方法。

频率网格间距

用户指定频率的一个常见问题是无意中选择了太粗糙的网格，这样显著的峰值位于网格点之间，并且完全丢失。

例子

假设您选择在100点处评估周期图：

>>> frequency = np.linspace(0.1, 1.9, 100)
>>> power = LombScargle(t, y, dy).power(frequency)
>>> plt.plot(frequency, power)   

(png, svg, pdf)

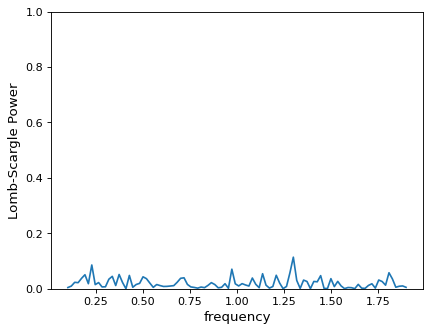
仅从这张图中，你就可以得出结论，数据中不存在明确的周期性信号。但这个结论是错误的：事实上有一个很强的周期信号，但周期图峰值落在所选网格点之间的间隙！

一种更可靠的方法是使用频率启发式来确定适当的网格间距，可以选择将最小和最大频率传递给 autopower() 方法：

>>> frequency, power = LombScargle(t, y, dy).autopower(minimum_frequency=0.1,
...                                                    maximum_frequency=1.9)
>>> len(frequency)
872
>>> plt.plot(frequency, power)   

(png, svg, pdf)

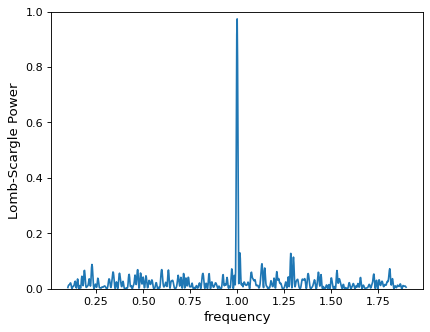
如果网格更细（这里有884个点在0.1到1.9之间），很明显数据中存在非常强的周期性信号。

默认情况下，启发式算法的目标是在每个显著的周期图峰值上有大约五个网格点；这可以通过改变 samples_per_peak 论点：

>>> frequency, power = LombScargle(t, y, dy).autopower(minimum_frequency=0.1,
...                                                    maximum_frequency=1.9,
...                                                    samples_per_peak=10)
>>> len(frequency)
1744

请记住，峰值宽度与观测基线成反比（即最大和最小时间之间的差），所需网格点数量将随基线的大小线性缩放。

Lomb疤痕模型

Lomb抖动周期图对每个频率下的数据拟合正弦模型，功率越大，拟合效果越好。考虑到这一点，在相位数据上绘制最佳拟合正弦曲线通常很有帮助。

例子

可以使用 model() 方法 LombScargle 对象：

>>> best_frequency = frequency[np.argmax(power)]
>>> t_fit = np.linspace(0, 1)
>>> ls = LombScargle(t, y, dy)
>>> y_fit = ls.model(t_fit, best_frequency)

然后，我们可以对数据进行阶段化处理，并绘制Lomb Scargle模型拟合图：

(png, svg, pdf)

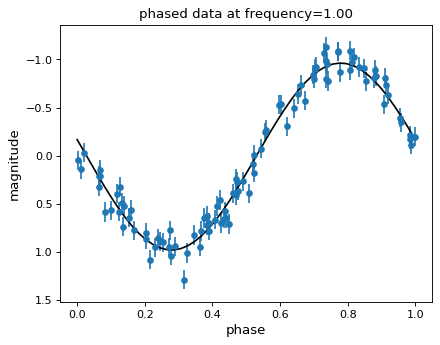
最佳拟合模型参数可以用 model_parameters() 方法 LombScargle 给定频率的对象：

>>> theta = ls.model_parameters(best_frequency)
>>> theta.round(2)
array([-0.01,  0.99,  0.11])

这些参数 \(\vec{{\theta}}\) 适用于以下型号：

\[y(t；f，\vec{\theta})=\theta_0+\sum_{n=1}^{\tt nterm} [\theta_{{2n-1}}\sin(2\pi n f t) + \theta_{{2n}}\cos(2\pi n f t)]\]

根据这些参数，可以通过计算 offset() ，这说明了数据的预中心化（即 center_data 参数），以及 design_matrix() ，为您计算正弦和余弦项：

>>> offset = ls.offset()
>>> design_matrix = ls.design_matrix(best_frequency, t_fit)
>>> np.allclose(y_fit, offset + design_matrix.dot(theta))
True

附加参数

初始化时， LombScargle 获取一些控制数据模型的附加参数：

• center_data (True by default) controls whether the y values are pre-centered before the algorithm fits the data. The only time it is really warranted to change the default is if you are computing the periodogram of a sequence of constant values to, for example, estimate the window power spectrum for a series of observations.

• fit_mean (True by default) controls whether the model fits for the mean of the data, rather than assuming the mean is zero. When fit_mean=True, the periodogram is more robust than the original Lomb-Scargle formalism, particularly in the case of smaller sample sizes and/or data with nontrivial selection bias. In the literature, this model has variously been called the date-compensated discrete Fourier transform, the floating-mean periodogram, the generalized Lomb-Scargle method, and likely other names as well.

• nterms (1 by default) controls how many Fourier terms are used in the model. As seen above, the standard Lomb-Scargle periodogram is equivalent to a single-term sinusoidal fit to the data at each frequency; the generalization is to expand this to a truncated Fourier series with multiple frequencies. While this can be very useful in some cases, in others the additional model complexity can lead to spurious periodogram peaks that outweigh the benefit of the more flexible model.

周期图规范化

在文献中发现了几种Lomb疤痕周期图的规范化方法。 LombScargle 通过 normalization 论点： normalization='standard' （违约）， normalization='model' ， normalization='log' 和 normalization='psd' . 这些规范化可以被认为是一个常数参考模型的最小二乘拟合 \(M_{{ref}}\) 周期模型 \(M(f)\) 在每一个频率上，用我们表示的残差的最佳拟合和 \(\chi^2_{{ref}}\) 和 \(\chi^2(f)\) 分别。

标准规范化

默认情况下，标准规范化周期图由恒定参考模型周围的数据残差进行标准化：

\[P{standard}（f）=\frac{\chi^2{ref}-\chi^2（f）}{\chi^2}{ref}\]

这种形式的规范化 (normalization='standard' )是中使用的默认选项 LombScargle . 产生的能量 P 是范围内的无量纲量 0≤P≤1 .

模型规范化

或者，周期图有时被周期模型周围的残差标准化：

\[P{model}（f）=\frac{\chi^2{ref}-\chi^2（f）}{\chi^2（f）}\]

这种形式的规范化可以用 normalization='model' . 如上所述，所产生的功率是一个无量纲的量，位于范围内 0≤P≤∞ .

对数归一化

标准化的另一种形式是按对数缩放周期图：

\[P{log}（f）=\log\frac{\chi^2{ref}}{\chi^2（f）}\]

此规范化可以用指定 normalization='log' ，得到的功率是范围内的无量纲量 0≤P≤∞ .

PSD标准化（未规范化）

最后，有时计算非标准化周期图是有用的 (normalization='psd' ）：

\[P{psd}（f）=\frac{1}{2}\左（\chi^2{ref}-\chi^2（f）\right）\]

在没有不确定性的情况下，将有单位 y.unit ** 2 . 此归一化可与标准傅里叶功率谱密度（PSD）进行比较：

>>> ls = LombScargle(t_days, y_mags, normalization='psd')
>>> frequency, power = ls.autopower()
>>> power.unit
Unit("mag2")

但是请注意 normalization='psd' 结果只有这些单位 如果未规定不确定性 . 在存在不确定性的情况下，即使是未规范化的PSD周期图也将是无量纲的；这是由于Lomb Scargle计算中的不确定性对数据进行了缩放：

>>> # with uncertainties, PSD power is unitless
>>> ls = LombScargle(t_days, y_mags, dy_mags, normalization='psd')
>>> frequency, power = ls.autopower()
>>> power.unit
Unit(dimensionless)

通过直接比较均匀采样输入的结果，可以确定PSD归一化周期图和Fourier PSD在非规范化、无不确定性情况下的等价性。

我们将首先定义一个方便函数来计算均匀采样量的基本傅里叶周期图：

>>> def fourier_periodogram(t, y):
...     N = len(t)
...     frequency = np.fft.fftfreq(N, t[1] - t[0])
...     y_fft = np.fft.fft(y.value) * y.unit
...     positive = (frequency > 0)
...     return frequency[positive], (1. / N) * abs(y_fft[positive]) ** 2

接下来，我们根据均匀采样数据计算两种版本的PSD：

>>> t_days = np.arange(100) * u.day
>>> y_mags = rand.standard_normal(100) * u.mag
>>> frequency, PSD_fourier = fourier_periodogram(t_days, y_mags)
>>> ls = LombScargle(t_days, y_mags, normalization='psd')
>>> PSD_LS = ls.power(frequency)

检查结果，我们发现两个输出匹配：

>>> u.allclose(PSD_fourier, PSD_LS)
True

这个周期的Fourier延拓被认为是scarlogle的一个原因。

有关这些规范化的统计特性的更多信息，请参见Baluev 2008 [8].

峰值显著性和虚警概率

备注

通过虚警概率解释Lomb陡坎峰值显著性是一个微妙的课题，下面计算的量通常被误解或误用。有关周期图峰值显著性的详细讨论，请参见 [11].

当使用Lomb抖动周期图来确定信号是否包含周期分量时，一个重要的考虑因素是周期图峰值的重要性。这种显著性通常用虚警概率表示，该概率编码在假定数据由无周期成分的高斯噪声组成的条件下，测量给定高度（或更高）峰值的概率。

例子

如果我们可以用周期性的周期波来模拟周期波，我们可以用一个周期性的周期信号来决定是否可以用一个周期性的周期信号来模拟：

>>> t = 100 * rand.random(60)
>>> dy = 1.0
>>> y = np.sin(2 * np.pi * t) + dy * rand.standard_normal(60)
>>> ls = LombScargle(t, y, dy)
>>> freq, power = ls.autopower()
>>> print(power.max())  
0.29154492887882927

周期图的峰值值为0.33，但这个峰值有多重要？我们可以用 false_alarm_probability() 方法：

>>> ls.false_alarm_probability(power.max())  
0.028959671719328808

这告诉我们，在假设数据中没有周期性信号的情况下，我们将在大约0.4%的时间内观察到一个如此高或更高的峰值，这表明数据中存在周期性信号。

备注

用户必须仔细解释这个概率：这是一个以假设没有信号为前提的测量；在符号中，你可以写下 \(P({{\rm data}} \mid {{\rm noise-only}})\) .

虽然看起来这个量可以用一个语句来解释，比如“这个数据只有0.4%的概率是噪声的”，但事实上 not 正确的陈述；在符号中，这个陈述描述数量 \(P({{\rm noise-only}} \mid {{\rm data}})\) 一般来说 \(P(A\mid B) \ne P(B\mid A)\) .

见 [11] 更详细地讨论这些警告。

我们还可能希望计算所需的峰值高度，以获得任何给定的虚警概率，这可以用 false_alarm_level() 方法：

>>> probabilities = [0.1, 0.05, 0.01]
>>> ls.false_alarm_level(probabilities)  
array([0.25681381, 0.27663466, 0.31928202])

这告诉我们，要达到10%的误报概率，最高周期图峰值约为0.25；5%需要0.27，1%需要0.32。

假警报近似值

虽然在任何特定频率下的虚警概率是可解析计算的，但是对于更相关的虚警水平量，没有封闭的解析表达式 最高 一个特定周期图中的峰值。这必须通过引导模拟来确定，或者通过各种方法进行近似。

astropy 提供了四个近似虚警概率的选项，可以使用 method 关键字：

• method="baluev" （默认值）实现Baluev 2008提出的近似值 [8], 它使用极值统计来计算无别名情况下的虚警概率的上界。实验表明，即使对于高混叠观测模式，该界也是有用的。

>>> ls.false_alarm_probability(power.max(), method='baluev')  
0.028959671719328808

• method="bootstrap" 实现了一个bootstrap模拟：它有效地在相同的观测时间内计算模拟数据上的许多Lomb抖动周期图。bootstrap方法可以非常精确地确定虚警概率，但是计算量非常大。估计虚警概率对应的水平 \(P_{{false}}\) ，需要订购 \(n_{{boot}} \approx 10/P_{{false}}\) 为单独的数据集计算周期。

>>> ls.false_alarm_probability(power.max(), method='bootstrap')  
0.0030000000000000027

• method="davies" 与Baluev方法相关，但在较大的虚警概率下会失去准确性。

>>> ls.false_alarm_probability(power.max(), method='davies')  
0.029387277355227746

• method="naive" 是一种基于周期图中分离良好的区域是独立的假设的基本方法。一般来说，它提供了一个非常差的错误警报概率估计，不应在实践中使用，但包含在完整性中。

>>> ls.false_alarm_probability(power.max(), method='naive')  
0.00810080828660202

下图比较了100个观测值峰值高度范围内的这些假警报估计值与严重混叠的观测模式：

(png, svg, pdf)

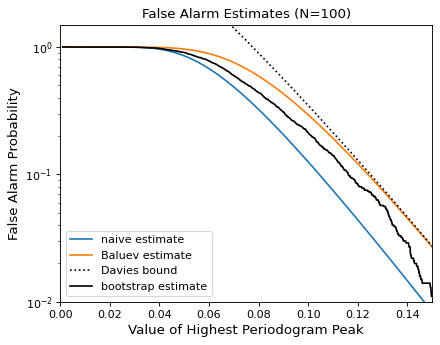
一般来说，当计算可行时，用户应该使用bootstrap方法，否则应该使用Baluev方法。

在所有这些方面，重要的是要记住一些注意事项：

• 虚警概率是根据一组特定的观测时间和特定的频率网格来计算的。

• 虚警概率是以没有周期成分的数据的零假设为条件的，尤其是对数据是否与周期模型实际一致没有定量的说明。

• 假警报概率与周期图中的最高峰值是否 对的 峰值，尤其是在具有强混叠模式的观测情况下并不是特别有用。

有关计算和解释假警报概率时的这些注意事项和其他注意事项的详细讨论，请参阅 [11].

周期图算法

这个 LombScargle 类提供了Lomb Scargle周期图的几个补充实现，可以使用 method Lomb Scargle power的关键字。通过设计，所有方法将返回相同的结果（一些近似值），并且每种方法都有其优缺点。

例如，使用Palmer（2009）的快速卡平方法计算周期图 [9], 您可以指定 method='fastchi2' ：

>>> frequency, power = LombScargle(t, y).autopower(method='fastchi2')

目前该软件包中有六种方法可用：

method='auto'

这个 auto 方法是默认值，它将尝试使用由输入数据驱动的启发式方法从以下方法中选择最佳选项。

method='slow'

这个 slow 方法是原始Lomb Scargle周期图的纯Python实现 ([1], [2]) ，以考虑观测噪声，并允许浮动平均值（有时称为 广义周期图 见 [10]) . 该方法不是特别快，缩放大约为 \(O[NM]\) 对于 \(N\) 数据点和 \(M\) 频率。

method='cython'

这个 cython 方法是Cython实现中使用的相同算法 method='slow' . 它比纯Python实现稍快一些，但随着输入大小的增加，内存效率大大提高。计算标度近似为 \(O[NM]\) 对于 \(N\) 数据点和 \(M\) 频率。

method='scipy'

这个 scipy 方法包装原始Lomb Scargle周期图的C实现，该实现在 scipy.signal.lombscargle() . 比这个稍微快一点 slow 方法，但不允许数据或扩展（如浮动平均数）中的错误。标度约为 \(O[NM]\) 对于 \(N\) 数据点和 \(M\) 频率。

method='fast'

这个 fast 方法是Press&Rybicki的快速周期图的纯Python实现 [3]. 它使用一个 外推法 利用快速傅里叶变换逼近周期图频率的方法。就像 slow 方法，它可以处理数据错误和浮动均值。标度约为 \(O[N\log M]\) 对于 \(N\) 数据点和 \(M\) 频率。快速算法以精度换取速度，并产生接近真实周期图的近似值。特别是，在某些情况下，你可能会观察到幂小于零。

method='chi2'

这个 chi2 方法是基于矩阵代数的纯Python实现（请参见 [7]) . 它利用了这样一个事实，即每个频率的Lomb抖动周期图相当于正弦曲线对数据的最小二乘拟合。优势 chi2 方法是允许将周期图扩展为多个Fourier项，由 nterms 参数。对于标准问题，它比 method='slow' 并按比例 \(O[n_fNM]\) 对于 \(N\) 数据点， \(M\) 频率，以及 \(n_f\) 傅立叶项。

method='fastchi2'

Palmer的快速卡方法（2009） [9] 相当于 chi2 方法，但矩阵是使用类似于 fast 方法。其结果是一个相对有效的周期图（尽管不如 fast 方法）可以扩展到多个术语。标度约为 \(O[n_f(M + N\log M)]\) 对于 \(N\) 数据点， \(M\) 频率，以及 \(n_f\) 傅立叶项。

总结

下表总结了上述算法的特点：

方法	计算标度	观测不确定性	偏差项（浮动平均值）	多重术语
"slow"	\(O[NM]\)	是的	是的	不
"cython"	\(O[NM]\)	是的	是的	不
"scipy"	\(O[NM]\)	不	不	不
"fast"	\(O[N\log M]\)	是的	是的	不
"chi2"	\(O[n_fNM]\)	是的	是的	是的
"fastchi2"	\(O[n_f(M + N\log M)]\)	是的	是的	是的

在计算缩放列中， \(N\) 是数据点的数量， \(M\) 是频率的数量，以及 \(n_f\) 是多项拟合的傅立叶项数。

RR天琴座示例

下图显示了为更真实的数据集计算周期图的示例。这里的数据包括对一颗类似于天琴座的变星的50次夜间观测，其光曲线形状比简单的正弦波更复杂：

(png, svg, pdf)

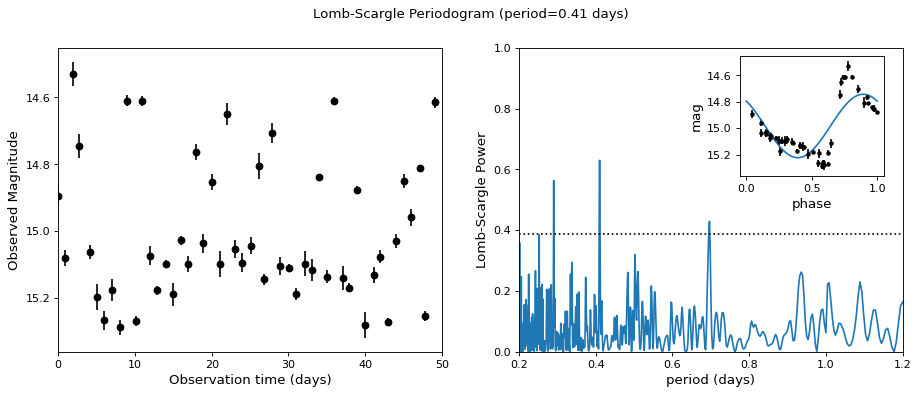
虚线显示与最大峰值虚警概率1%相对应的周期图水平。这个例子表明，对于不规则采样的数据，Lomb抖动周期图对高于平均Nyquist频率的频率非常敏感：以上数据以大约每晚一次观测的平均速率采样，周期图相对清晰地显示了0.41天的真实周期。

尽管如此，周期图仍有许多伪峰，这是由以下几个因素造成的：

1. 观测误差会导致真实峰值的功率泄漏。

2. 信号不是一个完美的正弦波，所以附加的峰值可以指示信号中的高频成分。

3. 观测仅在夜间进行，这意味着测量窗口的功率不可忽略，频率为每天1个周期。因此，我们希望别名出现在 \(f_{{\rm alias}} = f_{{\rm true}} + n f_{{\rm window}}\) 对于整数值 \(n\) . 真实周期为0.41天，观察窗内有1天信号，则 \(n=+1\) 和 \(n=-1\) 别名的周期分别为0.29天和0.69天：这些别名在上面的图中非常突出。

这些效应的相互作用意味着，在实践中，不能绝对保证最高峰值对应于最佳频率，必须仔细解释结果。有关这些效果的详细讨论，请参见 [11].

参考文献

[1] (1,2)

北卡罗来纳州洛姆市。 Least-squares frequency analysis of unequally spaced data . Ap&SS 39第447-462页（1976年）

[2] (1,2)

斯卡尔，J.D。 Studies in astronomical time series analysis. II - Statistical aspects of spectral analysis of unevenly spaced data . 亚太及日本地区1:263第835-853页（1982年）

[3] (1,2)

出版社W.H.和Rybicki，G.B， 非均匀采样数据谱分析的快速算法 . ApJ 1:338，第277页（1989年）

[4]

Vanderplas，J.，Connolly，A.Ivezic，Z.和Gray，A。 天体物理机器学习简介 . 智能数据理解会议（2012年）

[5]

Vanderplas，J.，Connolly，A.Ivezic，Z.和Gray，A。 天文学中的统计学、数据挖掘和机器学习 . 普林斯顿出版社（2014）}

[6]

范德普拉斯，J。 Gatspy：Python中天文时间序列的通用工具 （2015年）https://zenodo.org/record/14833

[7] (1,2)

VanderPlas，J.和Ivezic，Z。 多波段天文时间序列的周期图 . ApJ 812.1:18（2015年）

[8] (1,2)

巴鲁耶夫。 周期图峰值的统计显著性评估 MNRAS 3851279（2008年）

[9] (1,2)

帕默，D。 A Fast Chi-squared Technique for Period Search of Irregularly Sampled Data . ApJ 695.1:496（2009年）

[10]

Zechmeister，M.和Kurster，M。 The generalised Lomb-Scargle periodogram. A new formalism for the floating-mean and Keplerian periodograms ，A&A 496577-584（2009年）

[11] (1,2,3,4,5)

范德普拉斯，J。 Understanding the Lomb-Scargle Periodogram ApJS 236.1:16（2018年）https://ui.adsabs.harvard.edu/abs/2018ApJS..236…16V