稳健统计估计量#

稳健统计为复杂分布提供了可靠的基本统计估计。统计软件包包括几个在天文学中常用的强大的统计函数。这包括剔除离群值的方法以及底层分布的统计描述。

除了这里提到的函数外，模型还可以使用 FittingWithOutlierRemoval() .

西格玛裁剪#

西格玛裁剪提供了一种快速的方法来识别分布中的异常值。对于点的分布，计算中心和标准偏差。小于或超过与中心值的指定标准偏差数的值将被拒绝。可以迭代该过程以进一步拒绝异常值。

这个 astropy.stats 包为sigma裁剪提供了一个功能性和面向对象的接口。函数被调用 sigma_clip() 这个班叫做 SigmaClip . 默认情况下，它们都返回一个屏蔽数组，其中拒绝的点被屏蔽。

实例#

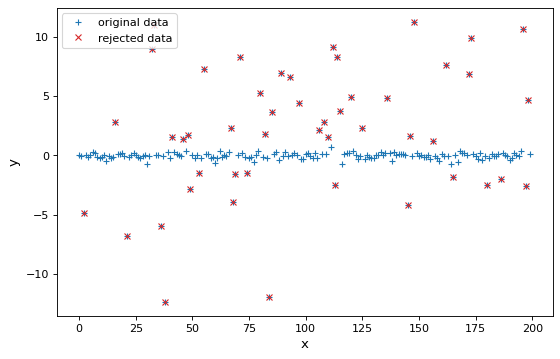
我们可以先生成一些平均值为0，标准偏差为0.2，但有异常值的数据：

>>> import numpy as np
>>> import scipy.stats as stats
>>> rng = np.random.default_rng(0)
>>> x = np.arange(200)
>>> y = np.zeros(200)
>>> c = stats.bernoulli.rvs(0.35, size=x.shape)
>>> y += (rng.normal(0., 0.2, x.shape) +
...       c * rng.normal(3.0, 5.0, x.shape))

现在我们可以使用 sigma_clip() 要对数据执行sigma剪裁：

>>> from astropy.stats import sigma_clip
>>> filtered_data = sigma_clip(y, sigma=3, maxiters=10)

然后，输出屏蔽数组可用于计算数据的统计信息、使模型适合数据，或以其他方式探索数据。

使用 SigmaClip 班级：

>>> from astropy.stats import SigmaClip
>>> sigclip = SigmaClip(sigma=3, maxiters=10)
>>> print(sigclip)  
<SigmaClip>
   sigma: 3
   sigma_lower: None
   sigma_upper: None
   maxiters: 10
   cenfunc: <function median at 0x108dbde18>
   stdfunc: <function std at 0x103ab52f0>
>>> filtered_data = sigclip(y)

注意一旦 sigclip 实例是在上面定义的，它可以应用于其他数据使用相同的已定义的sigma裁剪参数。

对于基本统计， sigma_clipped_stats() 是一个方便函数，用于计算数组的sigma剪裁平均值、中值和标准差。可以看出，拒绝离群值将返回基础分布的准确值。

使用 sigma_clipped_stats() 对于西格玛剪裁统计计算：

>>> from astropy.stats import sigma_clipped_stats
>>> y.mean(), np.median(y), y.std()  
(0.7068938765410144, 0.013567387681385379, 3.599605215851649)
>>> sigma_clipped_stats(y, sigma=3, maxiters=10)  
(-0.0228473012826993, -0.02356858871405204, 0.2079616996908159)

sigma_clip() 和 SigmaClip 可以与其他稳健统计相结合，以提供更好的异常值剔除。

import numpy as np
import scipy.stats as stats
from matplotlib import pyplot as plt
from astropy.stats import sigma_clip, mad_std

# Generate fake data that has a mean of 0 and standard deviation of 0.2 with outliers
rng = np.random.default_rng(0)
x = np.arange(200)
y = np.zeros(200)
c = stats.bernoulli.rvs(0.35, size=x.shape)
y += (rng.normal(0., 0.2, x.shape) +
      c * rng.normal(3.0, 5.0, x.shape))

filtered_data = sigma_clip(y, sigma=3, maxiters=1, stdfunc=mad_std)

# plot the original and rejected data
plt.figure(figsize=(8,5))
plt.plot(x, y, '+', color='#1f77b4', label="original data")
plt.plot(x[filtered_data.mask], y[filtered_data.mask], 'x',
         color='#d62728', label="rejected data")
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=2, numpoints=1)

(png, svg, pdf)

astropy.stats.sigma_剪裁模块#

功能#

`sigma_clip`(data[, sigma, sigma_lower, ...])	对提供的数据执行sigma裁剪。
`sigma_clipped_stats`(data[, mask, ...])	根据提供的数据计算sigma裁剪统计。

Classes#

SigmaClip([sigma, sigma_lower, sigma_upper, ...])

类来执行sigma裁剪。

类继承图#

绝对偏差中值#

中值绝对偏差（MAD）是一个分布范围的度量，定义为 median(abs(a - median(a))) . MAD可以用 median_absolute_deviation . 对于正态分布，MAD与标准差相关系数为1.4826，并且是一个方便函数， mad_std ，可用于应用转换。

备注

函数可以提供给 median_absolute_deviation 指定要在计算中使用的中值函数。根据NumPy的版本以及数组是否被屏蔽或包含不规则值，通过预先选择中值函数可以显著提高性能。如果没有指定中值函数， median_absolute_deviation 将尝试根据输入数据选择最相关的功能。

双权估计#

一组函数包含在 astropy.stats 使用biweight形式的包。这些函数长期以来被用于天文学，特别是用来计算星系团的速度色散 [1]. 以下一组任务可用于体重测量：

astropy.stats.biweight模块#

此模块包含使用Tukey的biweight函数计算稳健统计的函数。

功能#

`biweight_location`(data[, c, M, axis, ignore_nan])	计算重锤位置。
`biweight_scale`(data[, c, M, axis, ...])	计算体重秤。
`biweight_midvariance`(data[, c, M, axis, ...])	计算双权中方差。
`biweight_midcovariance`(data[, c, M, ...])	计算多变量对之间的双权中协方差。
`biweight_midcorrelation`(x, y[, c, M, ...])	计算两个变量之间的双权中间相关。