scipy.signal.lsim2¶
- scipy.signal.lsim2(system, U=None, T=None, X0=None, **kwargs)[源代码]¶
利用常微分方程求解器模拟连续时间线性系统的输出
scipy.integrate.odeint。- 参数
- 系统 :一个
lti类或描述系统的元组。对象的一个实例 下面给出了元组中的元素数量和解释:
1:(实例
lti)2:(Num,DEN)
3:(零、极、增益)
4:(A、B、C、D)
- UARRAY_LIKE(一维或二维),可选
描述每个时间T的输入的输入数组。在给定时间之间使用线性插值。如果有多个输入,则秩2数组的每一列代表一个输入。如果未给出U,则假定输入为零。
- TARRAY_LIKE(一维或二维),可选
定义输入和期望输出的时间步长。默认值为间隔上的101个等间距点 [0,10.0] 。
- X0ARRAY_LIKE(1D),可选
状态向量的初始条件。如果 X0 则假定初始条件为0。
- kwargsDICT
其他关键字参数将传递给函数 odeint 。有关更多详细信息,请参阅下面的注释。
- 系统 :一个
- 退货
- T一维ndarray
输出的时间值。
- youtndarray
系统的响应。
- xoutndarray
状态矢量的时间演化。
参见
注意事项
此函数使用
scipy.integrate.odeint来求解系统的微分方程。提供给的其他关键字参数lsim2传递给 odeint 。请参阅的文档scipy.integrate.odeint查看完整的参数列表。如果传入(num,den)作为
system,分子和分母的系数应按指数降序指定(例如s^2 + 3s + 5将表示为[1, 3, 5])。示例
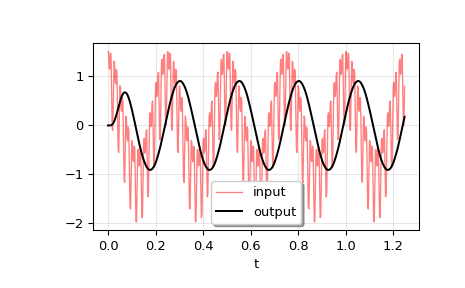
我们将使用
lsim2若要模拟应用于信号的模拟贝塞尔过滤,请执行以下操作。>>> from scipy.signal import bessel, lsim2 >>> import matplotlib.pyplot as plt
创建截止频率为12 Hz的低通贝塞尔过滤。
>>> b, a = bessel(N=5, Wn=2*np.pi*12, btype='lowpass', analog=True)
生成要应用过滤的数据。
>>> t = np.linspace(0, 1.25, 500, endpoint=False)
输入信号是频率为4 Hz、40 Hz和80 Hz的三条正弦曲线之和。过滤应该大部分消除40 Hz和80 Hz分量,只留下4 Hz信号。
>>> u = (np.cos(2*np.pi*4*t) + 0.6*np.sin(2*np.pi*40*t) + ... 0.5*np.cos(2*np.pi*80*t))
用来模拟过滤
lsim2。>>> tout, yout, xout = lsim2((b, a), U=u, T=t)
打印结果。
>>> plt.plot(t, u, 'r', alpha=0.5, linewidth=1, label='input') >>> plt.plot(tout, yout, 'k', linewidth=1.5, label='output') >>> plt.legend(loc='best', shadow=True, framealpha=1) >>> plt.grid(alpha=0.3) >>> plt.xlabel('t') >>> plt.show()
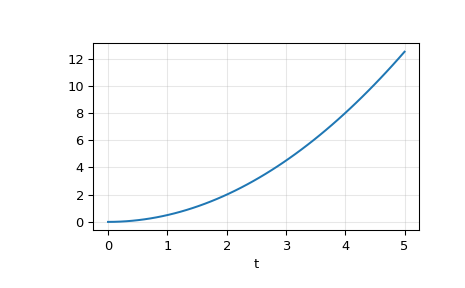
在第二个例子中,我们模拟一个双重积分器
y'' = u,具有恒定输入u = 1。我们将使用积分器的状态空间表示。>>> from scipy.signal import lti >>> A = np.array([[0, 1], [0, 0]]) >>> B = np.array([[0], [1]]) >>> C = np.array([[1, 0]]) >>> D = 0 >>> system = lti(A, B, C, D)
t 和 u 定义要模拟的系统的时间和输入信号。
>>> t = np.linspace(0, 5, num=50) >>> u = np.ones_like(t)
计算模拟,然后绘制 y 。不出所料,曲线图显示了曲线
y = 0.5*t**2。>>> tout, y, x = lsim2(system, u, t) >>> plt.plot(t, y) >>> plt.grid(alpha=0.3) >>> plt.xlabel('t') >>> plt.show()