scipy.special.jacobi¶
- scipy.special.jacobi(n, alpha, beta, monic=False)[源代码]¶
雅可比多项式。
定义为
\[(1-x^2)\frac{d^2}{dx^2}P_n^{(\alpha,\beta)} +(\β-\α-(\α+\β+2)x) \frac{d}{dx}P_n^{(\alpha,\beta)} +n(n+\α+\β+1)P_n^{(\α,\β)}=0\]为 \(\alpha, \beta > -1\) ; \(P_n^{{(\alpha, \beta)}}\) 是一次多项式 \(n\) 。
- 参数
- n集成
多项式的次数。
- alpha浮动
参数,必须大于-1。
- beta浮动
参数,必须大于-1。
- monic布尔值,可选
如果 True ,将前导系数缩放为1,默认值为 False 。
- 退货
- P正交1d
雅可比多项式。
注意事项
对于固定的 \(\alpha, \beta\) ,多项式 \(P_n^{{(\alpha, \beta)}}\) 是正交的吗? \([-1, 1]\) 带权重函数 \((1 - x)^\alpha(1 + x)^\beta\) 。
参考文献
- AS
米尔顿·阿布拉莫维茨和艾琳·A·斯特根主编。包含公式、图表和数学表的数学函数手册。纽约:多佛,1972年。
示例
雅可比多项式满足递归关系:
\[P_n^{(\α,\β-1)}(X)-P_n^{(\α-1,\β)}(X) =P_{n-1}^{(\α,\β)}(X)\]例如,可以针对以下情况验证这一点 \(\alpha = \beta = 2\) 和 \(n = 1\) 在间隔时间内 \([-1, 1]\) :
>>> import numpy as np >>> from scipy.special import jacobi >>> x = np.arange(-1.0, 1.0, 0.01) >>> np.allclose(jacobi(0, 2, 2)(x), ... jacobi(1, 2, 1)(x) - jacobi(1, 1, 2)(x)) True
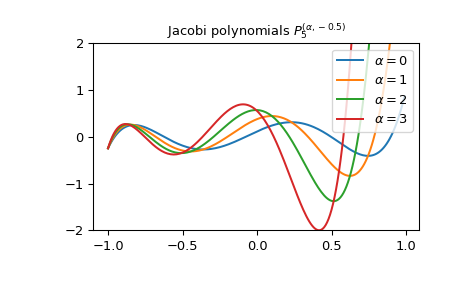
雅可比多项式的作图 \(P_5^{{(\alpha, -0.5)}}\) 对于不同的 \(\alpha\) :
>>> import matplotlib.pyplot as plt >>> import numpy as np >>> from scipy.special import jacobi >>> x = np.arange(-1.0, 1.0, 0.01) >>> fig, ax = plt.subplots() >>> ax.set_ylim(-2.0, 2.0) >>> ax.set_title(r'Jacobi polynomials $P_5^{(\alpha, -0.5)}$') >>> for alpha in np.arange(0, 4, 1): ... ax.plot(x, jacobi(5, alpha, -0.5)(x), label=rf'$\alpha={alpha}$') >>> plt.legend(loc='best') >>> plt.show()