scipy.special.chebyu

scipy.special.chebyu(n, monic=False)

第二类切比雪夫多项式。

定义为

\[(1-x^2)\frac{d^2}{dx^2}U_n-3x\frac{d}{dx}U_n +n(n+2)U_n=0；\]

\(U_n\) 是一次多项式 \(n\) 。

参数

n集成

多项式的次数。

monic布尔值，可选

如果 True ，将前导系数缩放为1，默认值为 False 。

退货

U正交1d

第二类切比雪夫多项式。

参见

chebyt

第一类切比雪夫多项式。

注意事项

多项式 \(U_n\) 是正交的吗？ \([-1, 1]\) 带权重函数 \((1 - x^2)^{{1/2}}\) 。

参考文献

AS

米尔顿·阿布拉莫维茨和艾琳·A·斯特根主编。包含公式、图表和数学表的数学函数手册。纽约：多佛，1972年。

示例

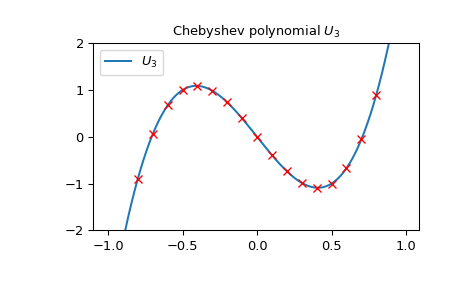
第二类切比雪夫多项式 \(n\) 可以获得作为特定的行列式的 \(n \times n\) 矩阵。作为一个例子，我们可以检查从下列行列式中获得的点是如何 \(3 \times 3\) 矩阵精确地铺设在 \(U_3\) ：

>>> import matplotlib.pyplot as plt
>>> from scipy.linalg import det
>>> from scipy.special import chebyu
>>> x = np.arange(-1.0, 1.0, 0.01)
>>> fig, ax = plt.subplots()
>>> ax.set_ylim(-2.0, 2.0)
>>> ax.set_title(r'Chebyshev polynomial $U_3$')
>>> ax.plot(x, chebyu(3)(x), label=rf'$U_3$')
>>> for p in np.arange(-1.0, 1.0, 0.1):
...     ax.plot(p,
...             det(np.array([[2*p, 1, 0], [1, 2*p, 1], [0, 1, 2*p]])),
...             'rx')
>>> plt.legend(loc='best')
>>> plt.show()

它们满足递归关系：

\[U_{2n-1}(X)=2T_n(X)U_{n-1}(X)\]

其中 \(T_n\) 是第一类切比雪夫多项式。我们来验证一下 \(n = 2\) ：

>>> from scipy.special import chebyt
>>> from scipy.special import chebyu
>>> x = np.arange(-1.0, 1.0, 0.01)
>>> np.allclose(chebyu(3)(x), 2 * chebyt(2)(x) * chebyu(1)(x))
True

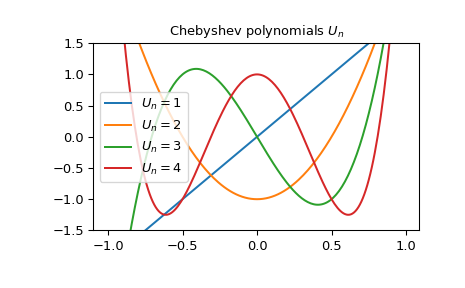
我们可以画出切比雪夫多项式 \(U_n\) 对于某些值， \(n\) ：

>>> import matplotlib.pyplot as plt
>>> from scipy.special import chebyu
>>> x = np.arange(-1.0, 1.0, 0.01)
>>> fig, ax = plt.subplots()
>>> ax.set_ylim(-1.5, 1.5)
>>> ax.set_title(r'Chebyshev polynomials $U_n$')
>>> for n in np.arange(1,5):
...     ax.plot(x, chebyu(n)(x), label=rf'$U_n={n}$')
>>> plt.legend(loc='best')
>>> plt.show()

上一页

scipy.special.chebyt

下一页

scipy.special.chebyc