scipy.interpolate.RBFInterpolator¶

class scipy.interpolate.RBFInterpolator(y, d, neighbors=None, smoothing=0.0, kernel='thin_plate_spline', epsilon=None, degree=None)[源代码]¶

N维的径向基函数(RBF)插值。

参数

y(P，N)类数组

数据点坐标。

d(P，.)类似数组

位于以下位置的数据值 y 。

neighbors整型，可选

如果指定，将仅使用这些最近的数据点来计算每个评估点的插值值。默认情况下使用所有数据点。

smoothing浮点或(P，)ARRAY_LIKE，可选

平滑参数。将其设置为0时，插值将与数据完美匹配。对于较大的值，插值逼近指定次数的多项式的最小二乘拟合。默认值为0。

kernel字符串，可选

RBF的类型。这应该是

‘线性’： -r

‘Thin_plate_Spline’： r**2 * log(r)

‘立方体’： r**3

“五行”： -r**5

‘多二次曲面’： -sqrt(1 + r**2)

‘INVERSE_MULTIQURIC’： 1/sqrt(1 + r**2)

‘逆向_二次’： 1/(1 + r**2)

“高斯”： exp(-r**2)

默认值为‘Thin_plate_Spline’。

epsilon浮动，可选

缩放RBF输入的形状参数。如果 kernel 为‘LINEAR’、‘THING_PLATE_SPLINE’、‘CUBLE’或‘QUINTIC’，此默认值为1，可以忽略，因为它与缩放平滑参数具有相同的效果。否则，必须指定此项。

degree整型，可选

相加多项式的次数。对于某些RBF，如果多项式次数太小，则插值可能不是适定的。这些RBF及其对应的最低学位为

‘多二次曲面’：0

‘线性’：0

‘Thin_plate_Spline’：1

‘立方体’：1

“五重奏”：2

默认值为的最小度数 kernel 如果没有最低学位，则为0。对于没有添加多项式的情况，将其设置为-1。

参见

NearestNDInterpolator
LinearNDInterpolator
CloughTocher2DInterpolator

注意事项

RBF是N维空间中的标量值函数，其值为 \(x\) 可以用以下方式来表示 \(r=||x - c||\) ，在哪里 \(c\) 是RBF的中心。

数据值向量的径向基函数插值 \(d\) ，它们来自不同的地点 \(y\) ，是以以下位置为中心的RBF的线性组合 \(y\) 加上指定次数的多项式。径向基函数插值函数写为

\[F(X)=K(x，y)a+P(X)b，\]

哪里 \(K(x, y)\) 是以以下位置为中心的RBF矩阵 \(y\) 在点数上进行评估 \(x\) ，以及 \(P(x)\) 是一个单项式矩阵，它跨越指定次数的多项式，计算结果为 \(x\) 。这些系数 \(a\) 和 \(b\) 是线性方程的解

\[(K(y，y)+\λi)a+P(Y)b=d\]

和

\[P(Y)^Ta=0，\]

哪里 \(\lambda\) 是一个非负平滑参数，它控制我们希望拟合数据的程度。当平滑参数为0时，数据完全拟合。

如果满足以下要求，则上述系统是唯一可解的：

\(P(y)\) 必须具有完整的列排名。 \(P(y)\) 在执行以下操作时，始终具有完整的列排名 degree 为-1或0。什么时候 degree 是1， \(P(y)\) 如果数据点位置不是全部共线(N=2)、共面(N=3)等，则具有完整的列排名。

如果 kernel 是“多二次”、“线性”、“薄板样条”、“三次”或“五次”，则 degree 不得低于上面列出的最小值。

如果 smoothing 为0，则每个数据点位置必须是不同的。

当使用不是尺度不变的RBF时(‘Multiquric’、‘Inverse_Multiquric’、‘Inverse_Quadatic’或‘Gauss’)，必须选择合适的形状参数(例如，通过交叉验证)。Shape参数的值越小，RBF越宽。当形状参数太小时，问题可能会变得病态或奇异。

求解RBF插值系数所需的内存随着数据点的数量呈二次曲线增加，当插值超过1000个数据点时，这可能变得不切实际。为了克服大型插值问题的内存限制， neighbors 可以指定参数，以便仅使用最近的数据点为每个评估点计算RBF插值。

1.7.0 新版功能.

参考文献

1: Fasshauer，G.，2007。基于Matlab的无网格逼近方法。世界科学出版公司。
2: http://amadeus.math.iit.edu/~fass/603_ch3.pdf
3: 瓦巴，G.，1990年。观测数据的样条模型。暹罗。
4: http://pages.stat.wisc.edu/~wahba/stat860public/lect/lect8/lect8.pdf

示例

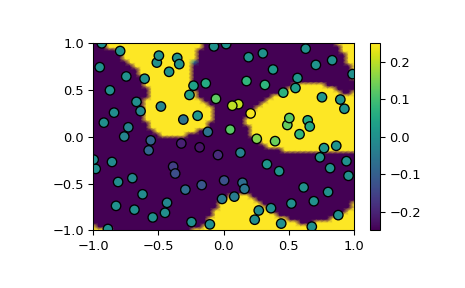
演示如何在2-D中将散乱的数据插值到网格中

>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import RBFInterpolator
>>> from scipy.stats.qmc import Halton

>>> rng = np.random.default_rng()
>>> xobs = 2*Halton(2, seed=rng).random(100) - 1
>>> yobs = np.sum(xobs, axis=1)*np.exp(-6*np.sum(xobs**2, axis=1))

>>> xgrid = np.mgrid[-1:1:50j, -1:1:50j]
>>> xflat = xgrid.reshape(2, -1).T
>>> yflat = RBFInterpolator(xobs, yobs)(xflat)
>>> ygrid = yflat.reshape(50, 50)

>>> fig, ax = plt.subplots()
>>> ax.pcolormesh(*xgrid, ygrid, vmin=-0.25, vmax=0.25, shading='gouraud')
>>> p = ax.scatter(*xobs.T, c=yobs, s=50, ec='k', vmin=-0.25, vmax=0.25)
>>> fig.colorbar(p)
>>> plt.show()

../../_images/scipy-interpolate-RBFInterpolator-1.png

方法：

__call__ \(X)

在以下位置对插值求值 x 。

scipy.interpolate.CloughTocher2DInterpolator.__call__

scipy.interpolate.RBFInterpolator.__call__