scipy.interpolate.CloughTocher2DInterpolator¶

class scipy.interpolate.CloughTocher2DInterpolator(points, values, fill_value=nan, tol=1e-06, maxiter=400, rescale=False)¶

CloughTocher2D插值器(点，值，TOL=1e-6)。

分段三次，C1光滑，2D中曲率最小化插值。

0.9 新版功能.

参数

pointsNdarray of Float，Shape(npoint，ndims)；或Delaunay: 数据点坐标或预计算的Delaunay三角剖分。
values浮动或复杂形状的ndarray(npoints，.): 数据值。
fill_value浮动，可选: 用于填充输入点凸包外部的请求点的值。如果未提供，则默认值为 nan 。
tol浮动，可选: 梯度估计的绝对/相对公差。
maxiter整型，可选: 梯度估计中的最大迭代次数。
rescale布尔值，可选: 在执行插值之前，重缩放指向单位立方体。如果某些输入尺寸具有不可公度的单位，并且相差许多量级，则此选项非常有用。

参见

griddata: 对非结构化的D-D数据进行插值。
LinearNDInterpolator: N>1维的分段线性插值。
NearestNDInterpolator: N>1维的最近邻插值。

注意事项

插值是通过使用Qhull三角化输入数据来构造的 [1], 在每个三角形上使用Clough-Tocher格式构造分段三次插值Bezier多项式 [CT]. 保证了插值函数连续可微。

选择插值的梯度，使得插值曲面的曲率近似最小化。执行此操作所需的渐变是使用中介绍的全局算法估计的 [Nielson83] 和 [Renka84].

参考文献

1: http://www.qhull.org/
CT: 例如，参见P.Alfeld的“用于四面体数据的三变量Clough-Tocher方案”。“计算机辅助几何设计”，1,169(1984)；G.Farin，“三角Bernstein-Bezier面片”。计算机辅助几何设计，3，83(1986)。
Nielson83: G.Nielson，“一种基于最小范数网络的插值散乱数据的方法”。数学课。比较，40,253(1983)。
Renka84: R·J·伦卡和A·K·克莱恩。“一种基于三角形的C1插值方法”，载“落基山数学学报”，14,223(1984)。

示例

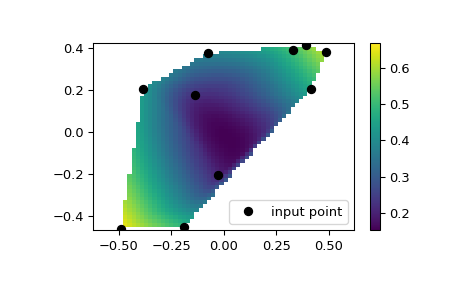
我们可以在2D平面上插入值：

>>> from scipy.interpolate import CloughTocher2DInterpolator
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> x = rng.random(10) - 0.5
>>> y = rng.random(10) - 0.5
>>> z = np.hypot(x, y)
>>> X = np.linspace(min(x), max(x))
>>> Y = np.linspace(min(y), max(y))
>>> X, Y = np.meshgrid(X, Y)  # 2D grid for interpolation
>>> interp = CloughTocher2DInterpolator(list(zip(x, y)), z)
>>> Z = interp(X, Y)
>>> plt.pcolormesh(X, Y, Z, shading='auto')
>>> plt.plot(x, y, "ok", label="input point")
>>> plt.legend()
>>> plt.colorbar()
>>> plt.axis("equal")
>>> plt.show()

../../_images/scipy-interpolate-CloughTocher2DInterpolator-1.png

方法：

__call__ \(xi)

在给定点评估插值器。

scipy.interpolate.NearestNDInterpolator.__call__

scipy.interpolate.CloughTocher2DInterpolator.__call__