4.2.5. 计算均方根量 MDAnalysis.analysis.rms
- 作者:
奥利弗·贝克斯坦,大卫·L·多特森,约翰·德特尔夫斯
- 年:
2016
- 版权所有:
GNU公共许可证v2
在 0.7.7 版本加入.
在 0.11.0 版本发生变更: 已添加 RMSF 分析。
在 0.16.0 版本发生变更: 重构RMSD以适应AnalysisBase API
该模块包含用于分析均方根量(如坐标均方根距)的代码 (RMSD )或按残差计算的均方根波动 (RMSF )。
本模块使用快速QCP算法 [Theobald2005] 要计算两个坐标集之间的均方根距离(RMSD)(如中实现的 MDAnalysis.lib.qcprot.CalcRMSDRotationalMatrix() )。
在已发表的作品中使用此模块时,请注明 [Theobald2005].
参见
MDAnalysis.analysis.align基于RMSD的结构对齐
MDAnalysis.lib.qcprot实现快速RMSD算法。
4.2.5.1. 示例应用程序
4.2.5.1.1. 计算多个域的RMSD
在这个例子中,我们将把一个蛋白质全局地匹配到一个参考结构上,并通过计算结构域相对于参考结构的RMSD来研究结构域的相对运动。这个例子是腺苷酸激酶的模糊轨迹,它采样了一个大的从闭合到开放的转变。该蛋白由核心、LID和NMP结构域组成。
使用主干原子叠加在封闭结构(轨迹的第0帧)上
计算核心、LID、NMP(主干原子)的主干RMSD和RMSD
弹道包含在测试数据文件中。中的数据 RMSD.results.rmsd 用来绘制 matplotlib.pyplot.plot() (见图 RMSD plot figure ):
import MDAnalysis
from MDAnalysis.tests.datafiles import PSF,DCD,CRD
u = MDAnalysis.Universe(PSF,DCD)
ref = MDAnalysis.Universe(PSF,DCD) # reference closed AdK (1AKE) (with the default ref_frame=0)
#ref = MDAnalysis.Universe(PSF,CRD) # reference open AdK (4AKE)
import MDAnalysis.analysis.rms
R = MDAnalysis.analysis.rms.RMSD(u, ref,
select="backbone", # superimpose on whole backbone of the whole protein
groupselections=["backbone and (resid 1-29 or resid 60-121 or resid 160-214)", # CORE
"backbone and resid 122-159", # LID
"backbone and resid 30-59"]) # NMP
R.run()
import matplotlib.pyplot as plt
rmsd = R.results.rmsd.T # transpose makes it easier for plotting
time = rmsd[1]
fig = plt.figure(figsize=(4,4))
ax = fig.add_subplot(111)
ax.plot(time, rmsd[2], 'k-', label="all")
ax.plot(time, rmsd[3], 'k--', label="CORE")
ax.plot(time, rmsd[4], 'r--', label="LID")
ax.plot(time, rmsd[5], 'b--', label="NMP")
ax.legend(loc="best")
ax.set_xlabel("time (ps)")
ax.set_ylabel(r"RMSD ($\AA$)")
fig.savefig("rmsd_all_CORE_LID_NMP_ref1AKE.pdf")
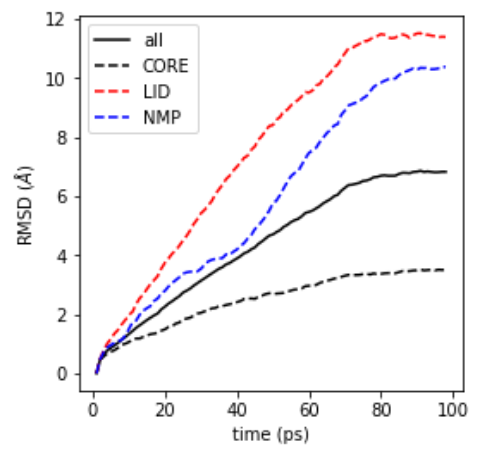
蛋白质的骨架和核心、LID、NMP结构域的RMSD图。
4.2.5.2. 功能
- MDAnalysis.analysis.rms.rmsd(a, b, weights=None, center=False, superposition=False)[源代码]
返回两个坐标集之间的RMSD a 和 b 。
a 和 b 是形状为N个原子的坐标的数组 \(N times 3\) 如由,例如,
MDAnalysis.core.groups.AtomGroup.positions()。备注
如果您使用在以下情况下执行的模拟的轨迹数据 周期边界条件 然后你 必须让你的分子完整 在执行RMSD计算之前,以使移动结构和参考结构的质心适当地重叠。
- 参数:
a (array_like) -- 要对齐的坐标 b
b (array_like) -- 要对齐的坐标(形状与 a )
weights (array_like (optional)) -- 带权重的一维阵列,用于计算加权平均
center (bool (optional)) -- 在计算之前减去几何图形的中心。以给定的权重计算加权平均为中心。
superposition (bool (optional)) -- 使用快速QCP算法执行旋转和平移叠加 [Theobald2005] 在计算RMSD之前;暗示
center=True。
- 返回:
rmsd --RMSD a 和 b
- 返回类型:
备注
RMSD \(\rho(t)\) 作为时间的函数计算为
\[\rho(T)=\Sqrt{\frac{1}{N}\sum_{i=1}^N w_i\Left(\mathbf{x}_i(T)) -\mathbf{x}_i^{\Text{ref}}\right)^2}\]它是当前配置(可能在最佳平移和旋转之后)相对于参考配置的配置空间中的欧几里德距离除以 \(1/\sqrt{{N}}\) 哪里 \(N\) 是坐标的个数。
重量 \(w_i\) 是根据输入权重计算的 weights \(w'_i\) 相对于平均数:
\[W_i=\frac{w‘_i}{\langw’\Rangle}\]示例
>>> import MDAnalysis as mda >>> from MDAnalysis.analysis.rms import rmsd >>> from MDAnalysis.tests.datafiles import PSF, DCD >>> u = mda.Universe(PSF, DCD) >>> bb = u.select_atoms('backbone') >>> A = bb.positions.copy() # coordinates of first frame >>> _ = u.trajectory[-1] # forward to last frame >>> B = bb.positions.copy() # coordinates of last frame >>> rmsd(A, B, center=True) 6.838544558398293
在 0.8.1 版本发生变更: center 已添加关键字
在 0.14.0 版本发生变更: superposition 已添加关键字
4.2.5.3. 分析类
- class MDAnalysis.analysis.rms.RMSD(atomgroup, reference=None, select='all', groupselections=None, weights=None, weights_groupselections=False, tol_mass=0.1, ref_frame=0, **kwargs)[源代码]
类对轨迹执行RMSD分析。
将计算两组原子的RMSD和轨迹中的所有帧 atomgroup 。通过应用选择选择来获得原子组 select 对于不断变化的 atomgroup 和固定的 reference 。
备注
如果您使用在以下情况下执行的模拟的轨迹数据 周期边界条件 然后你 必须让你的分子完整 在执行RMSD计算之前,以使所选结构和参考结构的质心适当地叠加。
使用以下选项运行分析
RMSD.run(),它将结果存储在数组中RMSD.results.rmsd。在 1.0.0 版本发生变更:
save()方法已移除,请使用np.savetxt()在……上面RMSD.results.rmsd取而代之的是。在 2.0.0 版本发生变更:
rmsd结果现在存储在MDAnalysis.analysis.base.Results实例。- 参数:
atomgroup (AtomGroup or Universe) -- 为其计算RMSD的原子组。如果轨迹与原子相关联,则计算在该轨迹上迭代。
reference (AtomGroup or Universe (optional)) -- 参考原子族;如果
None则当前帧的 atomgroup 是使用的。select (str or dict or tuple (optional)) -- 要操作的选择;可以是以下之一:1.任何有效的选择字符串
select_atoms()中产生相同选择的 atomgroup 和 reference 或2.一本词典{{'mobile': sel1, 'reference': sel2}}哪里 sel1 和 sel2 是应用于的有效选择字符串 atomgroup 和 reference 分别为(MDAnalysis.analysis.align.fasta2select()函数返回此类词典。 ClustalW 或 STAMP 序列比对);或3.元组(sel1, sel2)当使用2.或3.与 sel1 和 sel2 然后将这些选择字符串应用于 atomgroup 和 reference ,并应生成 等价原子团 。 sel1 和 sel2 每个都可以是一个 选择字符串列表 要生成一个AtomGroup具有定义的原子顺序,如下所述 有序选择 )。groupselections (list (optional)) -- 选项列表,如所述 select ,不同的是,这些选择是 总是适用于整个宇宙 ,即,
atomgroup.universe.select_atoms(sel1)和reference.universe.select_atoms(sel2)。每个选项都描述了要计算的其他RMSD 在结构叠加之后 根据 select 。不执行任何额外的拟合。每种选择的输出都包含一个附加列。。。注::实验性特征。仅实施了有限的错误检查。weights ({"mass",
None} or array_like (optional)) -- 1.“MASS”使用质量作为两者的权重 select 和 groupselections 。2.None将为两个原子平等地加权每个原子 select 和 groupselections 。3.如果与长度相同的一维浮点数组 atomgroup 时,请使用 array_like 作为中相应原子的权重 select ,并假设None为 groupselections 。weights_groupselections (False or list of {"mass",
Noneor array_like} (optional)) --1.
Falsewill apply imposed weights to groupselections fromweightsoption ifweightsis either"mass"orNone. Otherwise will assume a list of length equal to length of groupselections filled withNonevalues.2.{“MASS”,
None或ARRAY_LIKE},长度为 groupselections 将权重应用于 groupselections 相应地。tol_mass (float (optional)) -- 如果匹配原子的原子质量相差超过 tol_mass 。
ref_frame (int (optional)) -- 从中选择帧的帧索引 reference
verbose (bool (optional)) -- 如果设置为,则显示计算的详细进度
True;默认为False。
- 抛出:
SelectionError -- 如果从以下位置选择 atomgroup 和 reference 不匹配。
TypeError -- 如果 weights 或 weights_groupselections 不属于适当的类型;另请参阅
MDAnalysis.lib.util.get_weights()ValueError -- 如果 weights 与不兼容 atomgroup (长度不同)或不是一维数组(请参见
MDAnalysis.lib.util.get_weights())。一个ValueError的长度,也会引发 weights_groupselections 与不兼容 groupselections 。
备注
均方根偏差 \(\rho(t)\) 一群人 \(N\) 相对于参考结构的原子作为时间的函数被计算为
\[\rho(T)=\Sqrt{\frac{1}{N}\sum_{i=1}^N w_i\Left(\mathbf{x}_i(T)) -\mathbf{x}_i^{\Text{ref}}\right)^2}\]重量 \(w_i\) 是根据输入权重计算的 weights \(w'_i\) 相对于输入权重的平均值:
\[W_i=\frac{w‘_i}{\langw’\Rangle}\]选定的坐标来自 atomgroup 以最佳方式叠加(平移和旋转)在 reference 在每个时间步长进行协调,以使RMSD最小化。Douglas Theobald快速QCP算法 [Theobald2005] 用于旋转叠加并计算RMSD(请参见
MDAnalysis.lib.qcprot查看实施细节)。该类对输入运行各种检查,以确保可以比较这两个原子组。这包括原子质量的比较(即,只有相同质量的原子的位置才被认为是正确的比较)。如果不应该检查质量,只需设置 tol_mass 设置为一个较大的值,如1000。
参见
在 0.7.7 版本加入.
在 0.8 版本发生变更: groupselections 已添加
在 0.16.0 版本发生变更: 具有新功能的灵活加权方案 weights 关键字。
自 0.16.0 版本弃用: 而不是
mass_weighted=True(在0.17.0中删除)使用新的weights='mass';重构以适应AnalysisBase API在 0.17.0 版本发生变更: 已删除,已弃用 mass_weighted 关键词; groupselections 是 not 再旋转叠加在一起了。
在 1.0.0 版本发生变更: filename 关键字已删除。
- results.rmsd
包含RMSD的时间序列,为N×3
numpy.ndarray包含内容的数组[[frame, time (ps), RMSD (A)], [...], ...]。在 2.0.0 版本加入.
- rmsd
的别名
results.rmsd属性。自 2.0.0 版本弃用: 将在MDAnalysis 3.0.0中删除。请使用
results.rmsd取而代之的是。
- run(start=None, stop=None, step=None, frames=None, verbose=None, *, progressbar_kwargs={})
执行计算
- 参数:
start (int, optional) -- 分析的起始框架
stop (int, optional) -- 停止分析框架
step (int, optional) -- 要在每个分析的帧之间跳过的帧数
frames (array_like, optional) -- 用于切片轨迹的整数或布尔数组; frames 只能使用 instead 的 start , stop ,以及 step 。设置 both frames 并且至少有一项 start , stop , step 设置为非默认值将引发
ValueError。。。版本已添加::2.2.0verbose (bool, optional) -- 启用详细信息
progressbar_kwargs (dict, optional) -- 带有有关进度条位置等的自定义参数的ProgressBar关键字;请参见
MDAnalysis.lib.log.ProgressBar查看完整的列表。
在 2.2.0 版本发生变更: 添加了分析任意帧的功能,方法是在 frames 关键字参数。
在 2.5.0 版本发生变更: 增列 progressbar_kwargs 参数,允许修改tqdm进度条的描述、位置等
- class MDAnalysis.analysis.rms.RMSF(atomgroup, **kwargs)[源代码]
计算给定原子在轨道上的均方根函数。
备注
不执行RMSD叠加;假设用户正在提供其中感兴趣的蛋白质已经在结构上与参考结构对齐的轨迹(参见下面的示例部分)。蛋白质也是完整的,因为周期边界没有被考虑在内。
使用以下选项运行分析
RMSF.run(),它将结果存储在数组中RMSF.results.rmsf。- 参数:
- 抛出:
ValueError -- 如果计算出负值,则引发,这表示发生了数值溢出或下溢
备注
原子的均方根涨落 \(i\) 按时间平均值计算
\[\rho_i=\Sqrt{\Left\langle(\mathbf{x}_i-\langle\mathbf{x}_i\Rangle)^2\Right\Rangle}\]不执行质量加权。
此方法实现了一种计算平方和的算法,同时避免了溢出和下溢 [Welford1962] 。
示例
在本例中,我们通过分析以下参数来计算剩余均方根波动 \(\text{{C}}_\alpha\) 原子。首先,我们需要将轨迹与平均结构相匹配,作为参考。这需要首先计算平均结构。因为我们需要多次分析和操作相同的轨迹,所以我们将使用
MemoryReader。(如果你的轨迹不适合记忆,你需要 write out intermediate trajectories 存储到磁盘或 generate an in-memory universe 只包含蛋白质)::import MDAnalysis as mda from MDAnalysis.analysis import align from MDAnalysis.tests.datafiles import TPR, XTC u = mda.Universe(TPR, XTC, in_memory=True) protein = u.select_atoms("protein") # 1) the current trajectory contains a protein split across # periodic boundaries, so we first make the protein whole and # center it in the box using on-the-fly transformations import MDAnalysis.transformations as trans not_protein = u.select_atoms('not protein') transforms = [trans.unwrap(protein), trans.center_in_box(protein, wrap=True), trans.wrap(not_protein)] u.trajectory.add_transformations(*transforms) # 2) fit to the initial frame to get a better average structure # (the trajectory is changed in memory) prealigner = align.AlignTraj(u, u, select="protein and name CA", in_memory=True).run() # 3) reference = average structure ref_coordinates = u.trajectory.timeseries(asel=protein).mean(axis=1) # make a reference structure (need to reshape into a 1-frame # "trajectory") reference = mda.Merge(protein).load_new(ref_coordinates[:, None, :], order="afc")
我们创造了一个新的宇宙
reference它包含一个带有蛋白质平均坐标的单帧。现在我们需要通过最小化RMSD来将整个轨迹与参考轨迹相匹配。我们用MDAnalysis.analysis.align.AlignTraj::aligner = align.AlignTraj(u, reference, select="protein and name CA", in_memory=True).run()
轨迹现在与参考相适应(RMSD存储为 aligner.results.rmsd 以作进一步检查)。现在我们可以计算RMSF::
from MDAnalysis.analysis.rms import RMSF calphas = protein.select_atoms("name CA") rmsfer = RMSF(calphas, verbose=True).run()
和Plot::
import matplotlib.pyplot as plt plt.plot(calphas.resnums, rmsfer.results.rmsf)
引用
[Welford1962] (1,2,3)B. P. Welford. Note on a method for calculating corrected sums of squares and products. Technometrics, 4(3):419–420, 1962. doi:10.1080/00401706.1962.10490022.