2.6. 三维空间数据模型及结构#
近几年,很多人都在致力于三维数据模型的研究,虽然有三维GIS系统问世, 但其功能远远不能满足人们分析问题的需要。 原因主要是三维GIS理论不成熟,其拓扑关系模型一直没有解决,另外三维基础上的数据量很大, 很难建立一个有效的,易于编程实现的三维数据模型。 尽管如此,本节仍将介绍当前在三维GIS上所采用的几种数据模型。
3D空间构模方法研究是目前3D GIS领域以及3DGMS领域研究的热点问题。 许多专家学者在此领域做了有益的探索。 地质、矿山领域的一些专家学者,围绕矿床地质、工程地质和矿山工程问题, 对3DGMS的空间构建问题进行了卓有成效的理论与技术研究, 加拿大、澳大利亚、英国、南非等国还相继推出了一批在矿山和工程地质领域得到推广应用的3DGMS软件。
过去十来年中,研究提出了20余种空间构模方法。 若不区分准-3D和真-3D, 则可以将现有空间构模方法归纳为基于面模型(facialmodel)、基于体模型(volumetric model)和基于混合模型(nixedmodel)的3大类构模体系, 如表2-6所示(吴立新,2003)。
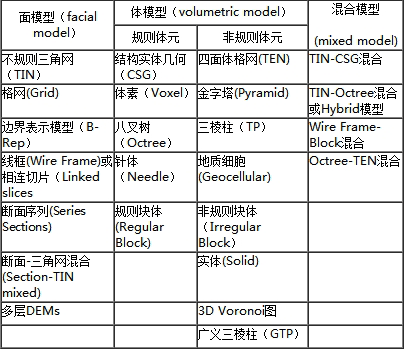
图 2.28 3D空间构模法分类#
三维矢量模型及结构#
三维矢量模型是二维中点、线、面矢量模型在三维中的推广。 它将三维空间中的实体抽象为三维空间中的点、线、面、体四种基本元素, 然后以这四种基本几何元素的集合来构造更复杂的对象。 以起点、终点来限定其边界,以一组型值点来限定其形状; 以一个外边界环和若干内边界环来限定其边界,以一组型值曲线来限定其形状; 以一组曲面来限定其边界和形状。 矢量模型能精确表达三维的线状实体、面状实体和体状实体的不规则边界,数据存储格式紧凑、数据量小, 并能直观地表达空间几何元素间的拓扑关系,空间查询、拓扑查询、邻接性分析、网络分析 的能力较强, 而且图形输出美观,容易实现几何变换等空间操作,不足之处是操作算法较为复杂,表达体内的不均一性的能力较差, 叠加分析实现较为困难,不便于空间索引。
1.3D FDS模型
Molennar(1992)在原二维拓扑数据结构的基础上,定义了结点(Node)、弧(Arc)、边(Edge)和面(Face)四种几何元素之间的拓扑关系及其与点(Point)、线(Line)、面(Surface)和体(Solid)四种几何目标之间的拓扑关系,并显式地表达点和体、线和体、点和面、线和面间的is-in,is-on等拓扑关系,提出了—种基于3D矢量图的形式化数据结构(FormalData Structure,FDS)(Pilout,Tempfli,Molenaar,1994),如图2-27所示。 其特点是显式地表达目标几何组成和矢量元素之间的拓扑关系, 有点类似于CAD中的BR表达与CSG表达的集成。
图 2.29 3DFDS数据结构(据Molenar,1992)#
这一模型的主要问题有三个:j仅考虑空间目标表面的划分和边界表达,没有考虑目标的内部结构, 因此只适合于形状规则的简单空间目标,难以表达地质环境领域,和的没有规则边界的复杂目标; k没有对空间实体间的拓扑关系进行严格的定义和形式化描述;l由于显示地存贮几何元素间的拓扑关系,使得操作不便。
2.三维边界(B-Rep)表示法
在形形色色的三维物体中,平面多面体在表示与处理上均比较简单,而且又可以用它来逼近其它各种物体。 平面多面体的每一个表面都可以看成是一个平面多边形。 为了有效地表示它们,总要指定它的顶点位置以及有哪些点构成边,哪些边围成一个面这样一些几何与拓扑的信息。 这种通过指定顶点位置、构成边的顶点以及构成面的边来表示三维物体的方法被称为三维边界表示法。
即三维边界(B-Rep)模型是通过面、环、边、点来定义形体的位置和形状,边界线可以是曲线, 也可以是空间曲线。 例如一个长方体由6个面围成,对应有6个环,每个环由4条边界定,每条边又由两个端点定义。
比较常用的三维边界表示法是采用三张表来提供点、边、面的信息,这三张表就是:顶点表, 用来表示多面体各顶点的坐标; 边表,指出构成多面体某边的两个顶点; 面表,给出围成多面体某个面的各条边。 对于后两个表,一般使用指针的方法来指出有关的边、点存放的位置。
三维边界模型的特点是: 详细记录了构成物体形体的所有几何元素的几何信息及其相互连接关系, 以便直接存取构成形体的各个面、面的边界以及各个顶点的定义参数, 有利于以面、边、点为基础的各种几何运算和操作。 边界表示构模在描述结构简单的3D物体时十分有效,但对于不规则3D地物则很不方便,且效率低下。
三维体元模型及结构#
真3D地学模拟、地面与地下空间的统一表达、陆地海洋的统一建模、3D拓扑描述、3D空间分析、3D动态地学过程模拟等问题, 已成为地学与信息科学的交叉技术前沿和攻关热点。
体模型基于3D空间的体元分割和真3D实体表达,体元的属性可以独立描述和存储, 因而可以进行3D空间操作和分析。 体元模型可以按体元的面数分为四面体(Tetrahedral)、六面体(Hexahedral)、棱柱体(Prismatic)和多面体(Polyhedral)共四种类型, 也可以根据体元的规整性分为规则体元和非规则体元两个大类。 规则体元包括CSG-tree、Voxel、Octree、Needle和RegularBlock共5种模型。 规则体元通常用于水体、污染和环境问题构模, 其中Voxel、Octree模型是一种无采样约束的面向场物质(如重力场、磁场)的连续空间的标准分割方法, Needle和RugularBlock可用于简单地质构模。 非规则体元包括TEN、Pyramid、TP、Geocelluar、IrregularBlock、Solid、3D-Voronoi和GTP共8种模型。 非规则体元均是有采样约束的、基于地质地层界面和地质构造的面向实体的3D模型。
1.八叉树(Octree)数据结构
八叉树数据结构可以看成是二维栅格数据中的四叉树在三维空间的推广。 该数据结构是将所要表示的三维空间V按X、Y、Z三个方向从中间进行分割,把V分割成八个立方
体; 然后根据每个立方体中所含的目标来决定是否对各立方体继续进行八等分的划分, 一直划分到每个立方体被一个目标所充满,或没有目标,或其大小已成为预先定义的不可再分的体素为止。
例如,图2-28所示的空间物体,其八叉树的逻辑结构可按图2-29表示。 图中,小圆圈表示该立方体未被某目标填满,或者说,它含有多个目标在其中,需要继续划分。 有阴影线的小矩形表示该立方体被某个目标填满,空白的小矩形表示该立方体中没有目标, 这两种情况都不需继续划分。
(a) 三维空间V中的物体 (b) 三维空间V及划分编码
图2-28 三维空间物体实例
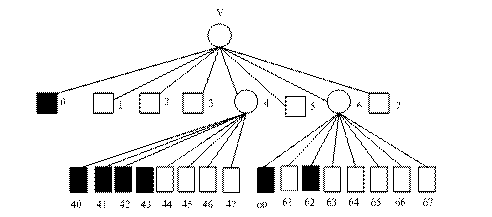
图 2.30 八叉树数据结构举例#
八叉树的主要优点在于可以非常方便地实现有广泛用途的集合运算(例如,可以求两个物体的并、交、差等运算), 而这些恰是其它表示方法比较难以处理或者需要耗费许多计算资源的地方。 不仅如此,由于这种方法的有序性及分层性,因而对显示精度和速度的平衡、隐线和隐面的消除等, 带来了很大的方便,特别有用。
2.四面体格网(TEN)
从理论上讲,对任意的三维物体,只要它满足一定的条件, 我们总可以找到一个合适的平面多面体来近似地表示这个三维物体,且使误差保持在一定的范围内。 一般地讲,如果要表示某个三维物体, 我们就须知道从这个物体表面S0上测得的一组点P1, P2,…PN的坐标。 其次,就是要为这些点建立起某种关系,这种关系有时被称为这些点代表的物体的结构。
通常这种近似(或叫逼近)有两种形式, 一种是以确定的平面多面体的表面作为原三维物体的表面S0的逼近; 另一种则是给出一系列的四面体,这些四面体的集合(又称为四面体格网)就是对原三维物体的逼近。 前者着眼于物体的边界表示(类似于三维曲面的表示),而后一类着眼于三维物体的分解, 就象一个三维物体可以用体素来表示一样。
四面体格网(TetrahedralNetwork-TEN)是将目标空间用紧密排列但不重叠的不规则四面体形成的格网来表示, 其实质是2DTIN结构在3D空间上的扩展。 在概念上首先将2D Voronoi格网扩展到3D,形成3DVornonoi多面体, 然后将TIN结构扩展到3D形成四面体格网。
1)四面体格网数据的组织
四面体格网由点、线、面和体四类基本元素组合而成。 整个格网的几何变换可以变为每个四面体变换后的组合,这一特性便于许多复杂的空间数据分析。 同时,四面体格网既具有体结构的优点,如: 快速几何变换,快速显示,又可以看成是一种特殊的边界表示,具有一些边界表示的优点,如: 拓扑关系的快速处理。
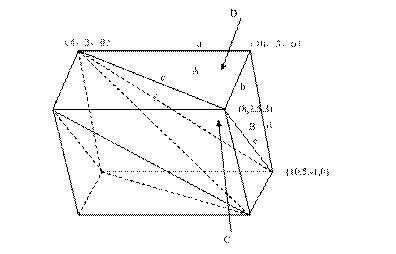
图 2.31 四面体格网表示三维空间物体的例子#
四面体 三角形
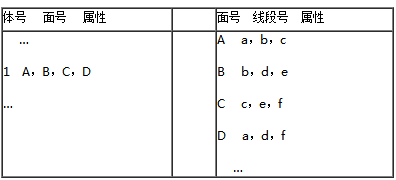
图 2.32 四面体格网表示三维空间物体的例子#
线 结点

图 2.33 数据结构#
用四面体格网表示三维空间物体的例子及其数据结构见图2-30和2-31。
四面体网格数据结构是网格生成程序实现上一个非常重要的问题。 网格数据结构的选择和建立,特别是能够满足各种各样网格生成算法要求的数据结构尤其显得重要。
2)四面体格网数据的生成算法
四面体格网(TEN)数据模型实质是二维三角形网(Triangulation IrregularNework-TIN)数据结构在三维上的扩展。 目前,主要有三种三角网生成的算法,即三角网生成算法[64],逐点插入法, 以及分治算法。 下面在分析三角网生成算法的基础上,给出了三个建立四面体格网的算法思想及步骤。
(1)四面体格网生成算法
该算法的思想是: 在数据场中先构成第一个四面体,然后以四面体的某个面向外扩展生成新的四面体, 直至全部离散点均已连成网为止。 其步骤如下:
① 在数据场中选择最近两个点连线,作为第一个三角形的一条边。
② 选择第三个点构成第一个三角形。
③ 选择第四个点构成第一个四面体。
④ i=1, j=1(i为已构成的四面体个数,j为正扩展的四面体个数)。
⑤ 扩展第j个四面体生成新的四面体0~4个。
⑥ i=i+k(k=0,1,2,4),j=j+1。
⑦ i≥j则转向⑤。
⑧ 结束。
上述算法实现过程中,在步骤②中,选择第三个点的依据是Delauny的两个性质。 其一是所选点与原两点一起所构成圆的圆心到原两点连线的“距离”最小; 其二是所选点与原两点连线的夹角最大。 在步骤③中, 选择第四个点的依据是所选点与已产生的三角形的三个点一起所构成球面的球心到三角形所构成的面的“距离”最小。
(2)逐次插入算法
该算法思想是:将未处理的点加入到已经存在的四面体格网中,每次插入一个点,然后将四面体格网进行优化。 其步骤如下:
① 生成包含所有数据点的立方体(即建立超四面体顶点)。
② 生成初始四面体格网。
③ 从数据中取出一点P加入到三角网中。
④ 搜寻包含点P的四面体,将P与此四面体的四个点相连,形成四个四面体。
⑤ 用LOP算法从里到外优化所有生成的四面体。
⑥ 重复③~⑤直至所有点处理完毕。
⑦ 删除所有包含一个或多个超四面体顶点的四面体。

图 2.34 四面体优化示意图#
优化前 优化后
上述步骤⑤中的LOP(Local OptimizationProcedure)是生成四面体格网的优化过程, 其思
想是运用四面体格网的性质,对由两个公共面的四面体组成的六面体进行判断,如果其中
一个四面体的外接球面包含第五个顶点,则将这个六面体的公共面交换,如图2-32所示。
(3)分治算法
该算法的思想是: 首先将数据排序,即将点集V按升序排列使(xi,yi, zi)<(xi+1,yi+1, zi+1), 不等式成立的条件是xi ≦xi+1且yi ≦yi+1 且zi <zi+1.然后递归地分割数据点集, 直至子集中只包含四个点而形成四面体,然后自下而上地逐级合并生成最终的四面体格网。 分治函数lee(V)内容如下:
lee(V)
① 把点集V分为近似相等的两个子集VL和VR。
② 分别在VL和VR中生成四面体格网。
如果VL中包含4~7个点,则建立VL的四面体格网; 否则调用lee(VL)。
如果VR中包含4~7个点,则建立VR的四面体格网; 否则调用lee(VR)。
③ 用局部优化算法LOP优化所产生的四面体格网。
④ 合并VL和VR中两个四面体格网。
分别生成VL和VR的凸多面体。
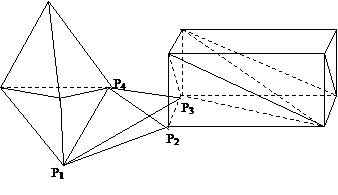
图 2.35 合并VL和VR示意图#
VL 四面体格网 VR四面体格网
在两多面体的Z方向底线寻找一三角形,然后建立一四面体。
从该四面体逐步扩展直至整个四面体格网建立完毕。
在合并VL和VR中两个四面体格网的过程中, 在建立第一个四面体,以及逐步扩展四面体时,均是在与已有数据点相连的顶点中寻找。 举例见图2-33,在合并VL和VR时, 先找到第一个三角形⊿P1P2P3, 然后从与P1,P2, P3相连的顶点中找到点P4, 即生成由P1P2P3P4这四个点所组成的四面体。 然后分别从⊿P1P2P4和⊿P1P3P4向外扩展, 对于⊿P1P2P4是在与点P1, P2,P4相连的点中寻找第四个点, 而⊿P1P3P4是在与点P1, P3,P4相连的点中寻找第四个点。 每找到一个点,必须确认四面体之间无交叉重叠,若出现这种情况,则放弃这个点,认为该三角形不能再扩展。
在算法实现过程中,数据结构的组织形式是有效建立四面体格网的关键,需要深一步的研究和探讨。
三维混合数据模型及结构#
基于面模型的构模方法侧重于3D空间实体的表面表示,如地形表面、地质层面等, 通过表面表示形成3D目标的空间轮廓,其优点是便于显示和数据更新,不足之处是难以进行空间分析。 基于体模型的构模方法侧重于3D空间实体的边界与内部的整体表示,如地层、矿体、水体、建筑物等, 通过对体的描述实现3D目标的空间表示,优点是易于进行空间操作和分析,但存储空间大,计算速度慢。 混合模型的目的则是综合面模型和体模型的优点,以及综合规则体元与非规则体元的优点,取长补短。
1.TIN-CSG混合构模
这是当前城市3DGIS和3DCM构模的主要方式,即以TIN模型表示地形表面,以CSG模型表示城市建筑物, 两种模型的数据是分开存储的。 为了实现TIN与CSG的集成,在TIN模型的形成过程中将建筑物的地面轮廓作为内部约束, 同时把CSG模型中建筑物的编号作为TIN模型中建筑物的地面轮廓多边形的属性, 并且将两种模型集成在一个用户界面(李清泉,1998; 孙敏等,2000)。 这种集成是一种表面上的集成方式,一个目标只由一种模型来表示,然后通过公共边界来连接, 因此其操作与显示都是分开进行。
2.TIN-Octree混合构模(Hybrid构模)
即以TIN表达3D空间物体的表面,以Octree表达内部结构。 用指针建立TIN和Octree之间的联系,其中TIN主要用于可视化与拓扑关系表达。 这种模型集中了TIN和Octree的优点,使拓扑关系搜索很有效, 而且可以充分利用映射和光线跟踪等可视化技术。 缺点是Octree模型数据必须随TIN数据的变化而改变,否则会引起指针混乱,导致数据维护困难。
3.Wire Frame-Block混合构模
即以WireFrame模型来表达目标轮廓、地质或开挖边界,以Block模型来填充其内部(惠勒A.J.等, 1989)。 为提高边界区域的模拟精度,可按某种规则对Block进行细分, 如以WireFrame的三角面与Block体的截割角度为准则来确定Block的细分次数(每次可沿一个方向或多个方向将尺寸减半)。 该模型实用效率不高,即每一次开挖或地质边界的变化都需进一步分割块体,即修改一次模型。
4.Octree-TEN混合构模
李德仁等曾提出过八又树(Octree)和不规则四面体(TEN)相结合的混合数据结构(李德仁等, 1997)。 在这个结构中,用八叉树作全局描述,而在八叉树的部分栅格内嵌入不规则四面体作局部描述。 这种结构特别适合于表达内部破碎、表面规整的二维对象,但对于表面也不规整的对象则不合适。
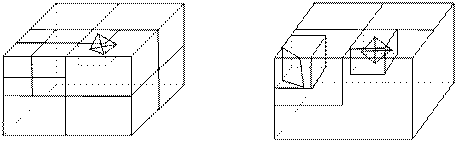
图 2.36 传统八叉树与TEN的结合,面八叉树与TEN的结合#
考虑将适合于表达实体内部破碎复杂结构的不规则四面体网和适合于表达表面不规整的八叉树层次结构有机结合起来, 形成统一的三维集成数据结构。 这种结构用八叉树结构
表达对象表面及其内部完整部分,并在八叉树的特殊标识结点内嵌入不规则四面体网表达对象内部的破碎部分, 整个结构用一棵经过有机集成的八叉树表达。 不规则四面体网和三级矢量化八叉树有机结合的统一三维集成数据结构,可用如图2-33、图2-34表示。
5.矢量与栅格集成模型
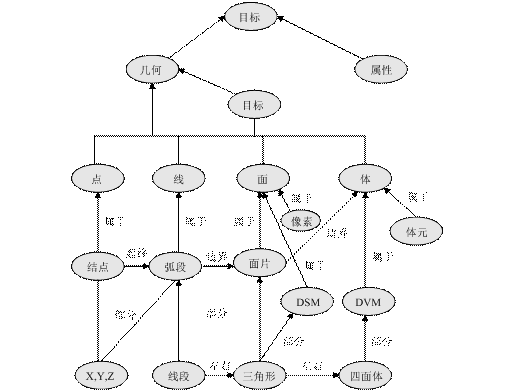
图 2.37 矢量栅格集成的三维空间数据模型(李清泉等,1998)#
一个三维空间数据模型应具有目标的几何、语义和拓扑描述;具有矢量和栅格数据结构; 能够从已有的二维GIS获取数据以及三维显示和表示复杂目标的能力。 矢量栅格集成的三维空间数据模型,如图2-36所示。
在这个模型中,空间目标分为四大类,即点(0D)、线(1D)、面(2D)和体(3D)。 目标的位置、形状大小和拓扑信息都可以得到描述。 其中目标的位置信息包含在空间坐标;目标的形状和大小信息包含在线、面和体目标; 目标的拓扑信息包含在目标的几何要素和几何要素之间的联系中,而且模型中包含矢量和栅格结构。 模型中包含的各种目标及其数据模型全面,但对具体的系统用什么样的数据模型可视需要而定。