7.1. 距离空间（度量空间）¶
距离在描述空间位置之间的关系时是一个十分重要的概念。 实际上GIS中距离的种类有多种，与之对应的抽象数学理论是本节的主要内容。
定义7.1 设X为任一非空集合，d: X×X→R为一函数，使得对于X的任何点x，y，z满足下列性质：
M1：d(x， y)≥0
M2：d(x， y)=0 : 
(x=y)
M3：d(x， y)=d(y， x) 
M4：d(x， y)≤d(x， z)+ d(z， y)
则(X， d)称为以d为距离的距离空间。 若x， y∈X，则实数d(x， y)称为从点x到点y的距离。 上面的性质中，M3称为对称性，M4称为三角不等式。
例： 对于可数无限维实数空间R 
， 定义距离函数d:
对空间中的任意两点p(x1， x2， …)和q(y1，
y2， …)， d(p， q)= 
，
这里 
和 
均收敛。
可以证明d(p，
q)一定收敛，(R ，d)满足距离空间定义。
(R ，d)称为希尔伯特(Hilbert)空间。
现在我们考察几种GIS中常用的距离及其与距离空间的关系。
最短线距离：沿地球球面从一个城市到另一个城市的最短距离。
球面曼哈顿距离：地球上两城市经度差与纬度差之和。
旅行时间：城市间旅行（假定沿公路线旅行）所需的最短时间。
考察上述距离定义，M1和M2显然为这三种距离所定义。 最短线距离和曼哈顿距离亦满足距离空间的对称性。 但旅行时间则不一定。 若考虑路面状况、地理特性（坡度等）、交通规则（单行线）等，则对称性不能满足。
三角不等式性质亦为最短线距离所满足。 对于旅行时间，三角不等式亦不一定满足。 图7-1所示，城市a和b及b和c间有高速公路，而a与c之间只有低等级公路，则就旅行时间而言，T(a， b)+T(b， c)≥T(a， c)不一定成立。
图 7.1 旅行时间与三角不等式¶
由上面的讨论，我们知道球面上的城市集合与最短线距离，以及曼哈顿距离均构成距离空间， 而与旅行时间则不能构成距离空间。 这说明
传统的距离空间（亦称度量空间）不能完全适应GIS
的需要。 特别需要说明的是，旅行时间这类的距离在
GIS应用中有很重要的意义。 例如，图7-2所示是
地震后的救灾问题。 救灾中心M需要在最短时间内赶
往灾区A、B、C、D、E，此时通常意义下的距离已不
重要，对称性、三角不等式难以满足，时间是最重要的。
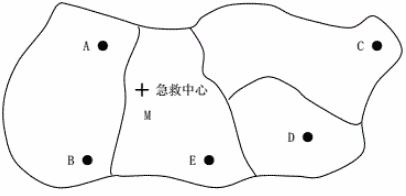
图 7.2 灾区与急救中心的位置¶