7.3. 基于集合的几何空间#
集合#
集合论是现代数学的基础。 虽然集合的基础理论没有为描述空间对象的性质及关系提供特殊的手段,但它仍是GIS的基础。 例如,一个地理区域(比如北京市)是另一地理区域的一部分(比如中国), 而这个地理区域本身又由另一些地理区域组成(比如海淀区、宣武区等)。 这正是集合间的包含关系。 事实上集合理论为描述一大类地理对象关系提供了方便的途径。
另外,在计算几何中,集合也是最基本的概念。 比如判定一个点是否落在一定区域内(元素与集合的隶属关系), 两个多边形叠加后的结果(两个集合的交集、补集、并集),等等。
下面我们简单回顾一下集合理论的一些基本概念。
- 集合:
由特定成员组成的一个整体称为一个集合,这些成员称为集合的元素。 \(x\) 是集合 \(A\) 的元素,记为 \(x∈A\) 。
集合是一个广泛的概念,对于计算机模型而言,集合通常是有限集或是可数集。
在经典集合论中,一个对象是否是一个集合的元素是确定的。 但对于GIS而言,较准确地反映一个元素属于一个集合的程度, 在一些情况下更为适用,这是模糊集合论的内容。 我们在后面的章节中将讨论这一问题。
- 空集合:
没有任何元素属于这个集合的集合称为空集合,记为 \(\emptyset\) :
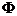 。
。
- 集合的包含与子集:
若集合B的每一元素也是集合A的元素,则称B包含于A,记作 \(B \subseteq A\) , B亦称为A的子集。
- 集合的相等:
若集合A与集合B有: \(A \subseteq B\) , \(B \subseteq A\) 同时成立, 则称集合A与集合B相等,记为 \(A=B\) 。
集合的基数:集合A的元素个数称为A的基数,记为 \(|A|\) 。
- 幂集:
设A为任意集合,P(A) 定义为 \(P(A)=\{x|x≤A\}\),P(A)称为A的幂集, 记为 \(2^A\) 。
- 集合的并:
设A,B是任意二个集合,集合 \(\{x | x∈A或x∈B\}\) 称为集合A与集合B的并集, 记为 \(A\cup B\) 。
集合的交: 设A,B是任意二个集合,集合 \(\{ x | x \in A 且 x \in B \}\) 称为集合A与B的交集, 记为 \(A \cap B\) 。
集合的差: 设A、B是任意二个集合,集合 \(\{ x | x \in A 且 x \notin B \}\) 称为A相对于B的差集, 记为 \(A-B\) 。
全集合:若集合A包含所讨论问题的全部元素,则称A为全集合,记为U。
集合的补:全集合U与集合A的差集,称为A的补集,记为 \(A'\)。
集合的对称差: 设集合A、B是任意二个集合, 集合 \(\{ x | x \in A 或 x \in B, 但 x \notin {A \cap B } \}\) 称为A与B的对称差。
图给出了集合的交、并、补运算的示意图。
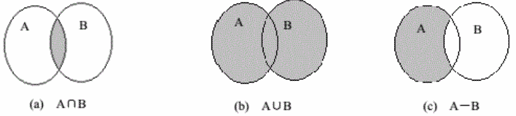
图 7.7 集合的交、并、补运算#
表7-1列出了本书中常用的集合符及表示符号,后面讨论中将直接引用。

图 7.8 常用集合#
关系#
关系是描述对象之间关联形式的数学概念,也是GIS中广泛使用的基本概念, 如点与点的邻接关系、面与面的相邻关系、几何对象之间的空间关系,等等。 这一部分我们简单介绍一下关系的定义和一些基本性质。
- 定义7.3
由几个具有给定次序的元素a1,a2,…, an组成的序列,成为有序n元组,记作: (a1,a2, …, an)。 当n=2时,称为序偶。
例如,欧氏平面的点(x,y)就是一个序偶,设距离采用欧氏距离, 则欧氏平面R2可以定义成所有实数序偶的集合,即R2={(x, y)| x,y ∈R}。
- 定义7.4
设A1,A2,…, An是任意集合,则称集合{ a1,a2, …,an| ai∈Ai,i=1,2, …,n}为集合A1,A2,…, An的笛卡尔积, 记为A1×A2×…×An。
例如,设A={f1,f2,…,fn},n∈N, 这里f1,f2,…,fn为n个多边形, B={c1,c2,…,cm},m∈N, 这里c1,c2,…,cm为m种不同颜色, 则A与B的笛卡尔积为:
A × B = {(f1, c1) , (f1, c2) , …,(f1, cm),
(f2, c1) , (f2, c2), …, (f2, cm),

(fn, c1) , (fn, c2),…, (fn, cm)}
可以看出,A×B实际上表述了各个多边形可能的所有着色。
定义7.5 设n∈N,A1,A2,…, An为任意n个集合, ρ≤A1×A2×…×An, 则称ρ为A1,A2,…,An间的n元关系, n=2时,称ρ为A1到A2的二元关系。 若A1=A2,则称ρ为A上的二元关系。
如前所述,关系表述的是对相间的关联模式。 实际应用中,二元关系经常使用。
例: A={f1, f2, f3}, f1,f2,f3为多边形,B={黄,红,蓝},B为三种颜色组成的集合。 则: A×B={(f1, 黄), (f1, 红), (f1, 蓝), (f2,黄), (f2, 红), ( f2, 蓝), (f3, 黄),(f3, 红), (f3, 蓝)}
ρ1={(f1, 黄), ( f2, 蓝), (f3,蓝)}
ρ2={(f1, 黄), (f1, 蓝), ( f2,蓝), (f3, 蓝)}
ρ3={(f1, 黄), ( f2, 蓝)}
由关系的定义可知,ρ1,ρ2, ρ3均是A到B的关系,它们表述的是f1, f2,f3可能的着色,其中ρ2, ρ3显然不是确定的着色方案, 因为ρ2中f1有两种着色, 而ρ3中f3没有着色。
关系的一些重要性质由定义7.6给出。
定义7.6 设ρ是A上的二元关系,
- 自反性:
若对于每个a∈A, 有(a, a)∈ρ, 则称ρ是自反的。
- 反自反性:
若对于每个a∈A, 有(a, a)
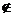 ρ, 则称ρ是反自反的。
ρ, 则称ρ是反自反的。
- 对称性:
若对于任意a, b∈A, 若(a, b)∈ρ, 则(b, a)∈ρ, 则称ρ为对称的。
- 反对称性:
若对于任意a, b∈A, 若(a, b)∈ρ, (b, a)∈ρ, 则a=b,则称ρ是反对称的。
- 传递性:
若对于任意的a,b,c∈A,若(a,b)∈ρ,(b,c)∈ρ,则(a,c)∈ρ,则称ρ是传递的。
上面这些关系的性质在描述空间对象之间的关系时经常用到。 图7-3-2(a)中连线表示旅游景点之间有公路连接的二元关系, (b)中带箭头的连线表示旅游景点与离其最近的旅游景点之间的二元关系。 (a)中的二元关系,满足对称性(若景点a到b有公路连接,则b到a有公路连接), 反自反性(景点到自身无公路连接)。 若我们将关系扩展为景点之间的可达关系(一个景点可通过公路到达另一景点), 则可达关系是自反的(假定景点到自身可达)、对称的(景点a到b可达, 则b到a可达)、传递的(景点a到b可达,b到c可达,则a到c可达)。
图7-11(b)表达的关系是反自反的(离一景点最近的景点不应是自身),对称性和传递性均不满足。 如图中所示,离景点a最近的景点是b,但离b最近的是c。 同样,离景点a最近的是b,离b最近的是c,显然c不是离a最近的景点。
- 定义7.7
若集合A上的关系ρ满足自反性、对称性、可传递性,则称ρ是等价关系。
如:在图7-11 (a)中定义的可达关系是等价关系。
- 定义7.8
若集合A上的关系ρ满足自反性、反对称性和传递性,则称ρ是A上的偏序关系。
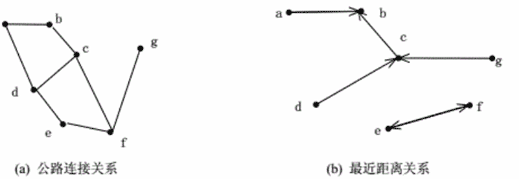
图 7.9 旅游景点之间的二元关系#
偏序关系也是一种常见的关系类型。 例如,地图中面与面的包含关系是自反的(任何面包含自身), 反对称的(若面f1包含面f2, 且f2包含f1, 则f1=f2), 传递的(若面f1包含面f2, 面f2包含f3, 则f1包含f3)。
函数#
函数是关系的一种特殊类型,由定义7.9给出。
- 定义7.9
设f是集合X到集合Y的一个关系,如果对每一个x∈X有唯一的y∈Y,使(x,y)∈f, 则称关系f为从X→Y的函数,记为f:X→Y,称x为自变量,y为f作用下x的象,记为y=f(x)
例: 令X={f1,f2,f3},Y={黄,红, 蓝},f1,f2,f3均为多边形。
ρ1={(f1, 黄), (f2, 黄), (f3,蓝)}
ρ2={(f1, 黄), (f2, 红), (f3,蓝)}
显然,ρ1和ρ2均是X→Y的函数。
对于函数f: X→Y,X称为f的定义域,记为dom f,Y称为f的值域包,集合{y | y∈Y, 且存在x∈X,使得y=f(x),称为f的值域,记为ran f。
图7-12给出了函数的直观形式。
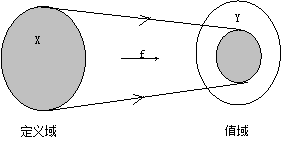
图 7.10 函数的直观形式#
- 定义7.10
设f: X→Y
若ran f =Y,即对Y中任一元素y,存在x∈X,使f(x)=y, 则称f为满射。
若对于任意x1, x2∈X,若x1≠x2, 则必有f(x1)≠f(x2),则称f为内射。
若f既是内射,又是满射,则称f为双射。
- 定义7.11
设f是X→Y的函数:
若存在函数g: ran f→X,使得对于任意x,有g(f(x))=x,则称f是左可逆的,并称g为f的左逆函数。
若存在函数g:Y→X,使得对于任意y∈Y,有f(g(y))=y,则称f使右可逆的,并称g为f的右逆函数。
若函数g: Y→X,使(1),(2)同时成立,则称f是可逆的,并称g为f的逆函数,记作f:sup:`-`1。
内射、满射、双射以及逆函数是函数的一些基本性质,由定义7.11可以证明:
函数f左可逆当且仅当f为内射。
函数f右可逆当且仅当f为满射。
函数f可逆当且仅当f为双射。
这里不作证明。
凸集#
前面我们给出了凸多边形的定义,这一部分我们从集合论的角度来讨论多边形的凸特性。
- 定义7.12
设S是欧氏平面的点集,x,y∈S,若从连接x到y的线段上的点均属于S或x=y, 则称点x从点y是可见的。
- 定义7.13
设S是欧氏平面的点集,x∈S,x称为S的观察点,当且仅当对S中的任一点y从x都是可见的。
- 定义7.14
设S是欧氏平面的点集,若S中存在一个观察点,则称S是半凸的。
显然星形多边形是半凸集。
- 定义7.15
设S是欧氏平面的点集,S称为凸集,当且仅当S中的每一个点都是S的一个观察点。
图7-13给出了点x,y,z 之间的可见特性。 从y 可见x和z,但x和z互不可见。
由可见性的定义可知,点集S 中的可见性是S上的一个二元关系, 它满足自反性(从点x可见x自身)、对称性(点x可见y,则y必定可见x), 但不满足传递性,图7-14中, x可见y,y可见z,但x不可见z。
由定义7.14,3.15,我们可以把多边形分成三大类:非半凸多边形、半凸多边形、凸多边形。 图7-14分别给出了一个实例。
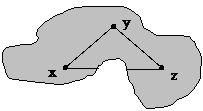
图 7.11 点x, y, z之间的可见性#
需要注意的是,任意两个凸集的交仍是凸集,据此可以给出一个点集的凸壳的定义。
- 定义7.16
点集S的凸壳 (Convex Hull) 定义为包含S的所有凸集的交集。
实际上S的凸壳即是包含S的最小凸集。 可以证明,一个有限点集的凸壳一定是一个凸多边形。 图7-15给出了一个点集的凸壳的实例。 凸壳在GIS和 计算几何中是一个十分重要的概念,在GIS中可能对应覆盖某几个城市的最小区域。

图 7.12 多边形的三种类型#
计算几何中对求解一个点集的凸壳的算法有专门的研究,我们在以后的相关章节中还要详细讨论凸壳。

图 7.13 点集的凸壳#