8.4. 叠置分析#
叠置分析是GIS用户经常用以提取数据的手段之一。 该方法源于传统的透明材料叠加,即将来自不同数据源的图纸绘于透明纸上,在透光桌上将图纸叠放在一起, 然后用笔勾绘感兴趣的部分(即提取感兴趣的数据)。 地图的叠置,按直观概念就是将两幅或多幅地图重迭在一起,产生新数据层和新数据层上的属性。 新数据层或新空间位置上的属性就是各叠置地图上相应位置处各属性的函数。
一般情况下,为便于管理和应用开发地理信息(空间信息和属性信息),在建库时是分层进行处理的。 也就是说,根据数据的性质分类,性质相同的或相近的归并到一起,形成一个数据层。 例如,对于一个地形图数据库来说,可以将所有建筑物作为一个数据层,所有道路作为一个数据层, 地下管线井作为另一个数据层等等。 我们经常要将各数据层综合起来作分析,如对各管线井求取离它最近的道路并计算它离最近道路的距离, 这类问题就需要对多层数据实施叠置来产生具有新特征的数据层。
栅格系统的叠加分析#
栅格数据来源复杂,包括各种遥感数据、航测数据、航空雷达数据、各种摄影的图像数据, 以及数字化和网格化的地质图、地形图、各种地球物理、地球化学数据和其它专业图像数据。 叠加分析操作的前提是要将其转换为统一的栅格数据格式,且各个叠加层必须具有统一的地理空间, 即具有统一的空间参考(包括地图投影、椭球体、基准面等),统一的比例尺以及具有统一的分辨率(刘湘南, 2005)。
栅格叠加可以用于数理统计,如行政区划图和土地利用类型图叠加, 可计算出某一行政区划内的土地利用类型个数以及各种土地利用类型的面积; 可进行益本分析,即计算成本、价值等,如城市土地利用图与大气污染指数分布图、道路分布图叠加, 可进行土地价格的评估与预测; 可进行最基本的类型叠加,如土壤图与植被图叠加,可得出土壤与植被分布之间的关系图; 可以进行动态变化分析以及几何提取等应用; 在各类地质综合分析中,栅格方式的叠置分析也十分有用,很多种类的原始资料如化探资料、微磁资料等等, 都是离散数据,容易转换成栅格数据,因而便于栅格方式的叠置分析。 另外由于没有矢量叠加时产生细碎多边形的问题(这一点下面会详细解释), 栅格方式的叠置产生的结果有时更为合理。
在栅格系统中,层间叠加可通过像元之间的各种运算来实现。 设A,B,C等表示第一、第二、第三等各层上同一坐标处的属性值,f函数表示各层上属性与用户需要之间的关系, U为叠置后属性输出层的属性值,则
U=f(A,B,C……)
叠加操作的输出的结果可能是:各层属性数据的平均值(简单算术平均或加权平均等);
各层属性数据的最大值或最小值;算术运算结果;逻辑条件组合等。
基于不同的运算方式和叠加形式,栅格叠加变换包括如下几种类型(刘湘南,2005):
(1)局部变换:基于像元与像元之间一一对应得运算,每个像元都是基于它自身的运算,不考虑其他的与之相邻的像元。
(2)邻域变换:以某一像元为中心,将周围像元的值作为算子,进行简单求和、求平均值、最大值、最小值等。
(3)分带变换:将具有相同属性值的像元作为整体进行分析运算。
(4)全局变换:基于研究区域内所有像元的运算,输出栅格的每一个像元值是基于全区的栅格运算,这里像元是具有或没有属性值的栅格。
1.局部变换
每一个像元经过局部变换后的输出值与这个像元本身有关系,而不考虑围绕该像元的其他像元值。 如果输入单层格网,局部变换以输入格网像元值的数学函数计算输出格网的每个像元值,如图8-12所示。 单层格网的局部变换可以是基本的代数运算,也可以是三角函数、指数、对数、幂等运算来定义其函数关系。 多层格网的局部变换与把空间和属性结合起来的矢量地图叠置类似,但效率更高。 输出栅格层的像元值可由多个输入栅格层的像元值或其频率的量测值得到,如图8-13。 概要统计(包括最大值、最小值、值域、总和、平均值、中值、标准差等)也可用于栅格像元的测度。 例如,用最大统计量的局部变换运算可以从代表20年降水变化的20个输入栅格层计算一个最大降水量格网, 这20个输入栅格层中的每个像元都是以年降水数据作为其像元值。
输入栅格 输出栅格
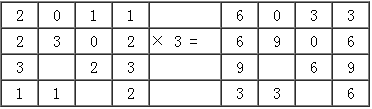
图 8.12 单层局部变换#
- 输入栅格
乘数栅格 输出栅格

图 8.13 多层局部变换#
2.邻域变换
邻域变换输出栅格层的像元值主要与其相邻像元值有关。 如果要计算某一像元的值,就将该像元看作一个中心点,一定范围内围绕它的格网可以看作它的辐射范围, 这个中心点的值取决于采用何种计算方法将周围格网的值赋给中心点,其中的辐射范围可自定义。 若输入栅格在进行邻域求和变换时定义了每个像元周围3×3个格网的辐射范围, 在边缘处的像元无法获得标准的格网范围,辐射范围就减少为2×2个格网,如图8-14所示。 那么,输出栅格的像元值就等于它本身与辐射范围内栅格值之和。 比如,左上角栅格的输出值就等于它和它周围像元值2、0、2、3之和7。
中心点的值除了可以通过求和得出之外,还可以取平均值、标准方差、最大值、最小值、极差频率等。 邻域变换中的辐射范围一般都是规则的方形格网,也可以是任意大小的圆形、环形和楔形。 圆形邻域是以中心点像元为圆心,以指定半径延伸扩展; 环形或圈饼状邻域是由一个小圆和一个大圆之间的环形区域组成; 楔形邻域是指以中心点单元为圆心的圆的一部分。
邻域变换的一个重要用途是数据简化。 例如,滑动平均法可用来减少输入栅格层中像元值的波动水平,该方法通常用3×3或5×5矩形作为邻域, 随着领域从一个中心像元移到另一个中心像元,计算出在邻域内的像元平均值并赋予该中心像元, 滑动平均的输出栅格表示初始单元值的平滑化。 另一个例子是以种类为测度的领域运算,列出在邻域之内有多少不同单元值,并把该数目赋予中心像元, 这种方法用于表示输出栅格中植被类型或野生物种的种类。
输入栅格 输出栅格
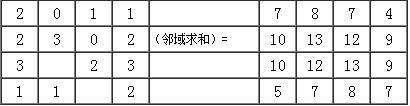
图 8.14 邻域变换#
3.分带变换
将同一区域内具有相同像元值得格网看作一个整体进行分析运算,称为分带变换。 区域内属性值相同的格网可能并不毗邻,一般都是通过一个分带栅格层来定义具有相同值的栅格。 分带变换可对单层格网或两个格网进行处理,如果为单个输入栅格层,分带运算用于描述地带的几何形状, 诸如面积、周长、厚度和矩心。 面积为该地带内像元总数乘以像元大小。 连续地带的周长就是其边界长度,由分离区域组成的地带,周长为每个区域的周长之和。 厚度以每个地带内可画的最大圆的半径来计算。 矩心决定了最近似于每个地带的椭圆形的参数,包括矩心、主轴和次轴。 地带的这些几何形状测度在景观生态研究中尤为有用。
多层栅格的分带变换如图8-15所示,通过识别输入栅格层中具有相同像元值得格网在分带栅格层中的最大值, 将这个最大值赋给输入层中这些格网导出并存储到输出栅格层中。 输入栅格层中有4个地带的分带格网,像元值为2的格网共有5个,它们分布于不同的位置并不相邻, 在分带栅格层中,它们的值分别为1、5、8、3和5,那么取最大的值8赋给输入栅格层中像元值为2的格网, 原来没有属性值的格网仍然保持无数据。 分带变换可选取多种概要统计量进行运算,如平均值、最大值、最小值、总和、值域、标准差、中值、
- 输入栅格
分带栅格 输出栅格
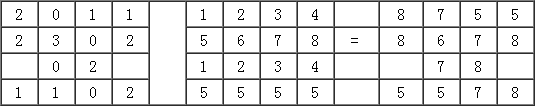
图 8.15 分带变换#
多数、少数和种类等,如果输入栅格为浮点型格网,则无最后四个测度。
4.全局变换
全局变换是基于区域内全部栅格的运算,一般指在同一网格内进行像元与像元之间距离的量测。 自然距离量测运算或者欧几里德几何距离运算属于全局变换, 欧几里德几何距离运算分为两种情况:一种是以连续距离对源像元建立缓冲,在整个格网上建立一系列波状距离带; 另一种是对格网中的每个像元确定与其最近的源像元的自然距离,这种方式在距离量测中比较常见。
欧几里德几何距离运算首先定义源像元,然后计算区域内各个像元到最近的源像元的距离。 在方形网格中,垂直或水平方向相邻的像元之间的距离等于像元的尺寸大小或者等于两个像元质心之间的距离; 如果对角线相邻,则像元距离约等于像元的尺寸大小的1.4倍; 如果相隔一个像元那么它们之间的距离就等于像元大小的2倍,其他像元距离依据行列来计算。 如图8-16中,输入栅格有两组源数据,源数据1是第1组,共有三个栅格,源数据2组只有一个栅格。 欧几里德几何距离定义源像元为0值,而其他像元的输出值是到最近的源距离像元的距离。 因此,如果默认像元大小为1个单位的话,输出栅格中的像元值就按照距离计算原则赋值为0、1、1.4或2。
输入栅格 输出栅格
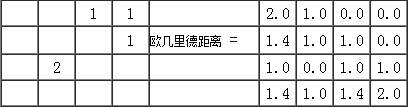
图 8.16 欧几里德距离运算#
5.栅格逻辑叠加
栅格数据中的像元值有时无法用数值型字符来表示,不同专题要素用统一的量化系统表示也比较困难, 故使用逻辑叠加更容易实现各个栅格层之间的运算。 比如某区域土壤类型包括黑土、盐碱土以及沼泽土,也可获得同一地区的土壤pH值以及植被覆盖类型相关数据, 要求查询出土壤类型为黑土、土壤pH值<6且植被覆盖以阔叶林为主的区域,将上述条件转换为条件查询语句, 使用逻辑求交即可查询出满足上述条件的区域。
二值逻辑叠加是栅格叠加的一种表现方法,用0和1分别表示假(不符合条件)与真(符合条件)。 描述现实世界中的多种状态仅用二值远远不够,使用二值逻辑叠加往往需要建立多个二值图, 然后进行各个图层的布尔逻辑运算,最后生成叠加结果图。 符合条件的位置点或区域范围可以是栅格结构影像中的每一个像元,或者是四叉树结构影像中的每一个像块, 也可以是矢量结构图中的每一个多边形。
图层之间的布尔逻辑运算包括:与(AND)、或(OR)、非(NOT)、异或(XOR)等。
(1)与(&):比较两个或两个以上栅格数据图层,如果对应的栅格值均为非0值,则输出结果为真(赋为1),否则输出结果为假(赋值为0)。
(2)或(|):比较两个或两个以上栅格数据图层,对应的栅格值中只有一个或一个以上为非0值,则输出结果为真(赋为1),否则输出结果为假(赋值为0)。
(3)非(^):对一个栅格数据图层进行逻辑“非”运算,如果栅格值为0值,则输出结果为真(赋为1); 如果栅格值为非0值,则输出结果为假(赋值为0)。
(4)异或(!):比较两个或两个以上栅格数据图层,如果对应的栅格值在逻辑真假互不相同(一个为0,另一个为非0值),则输出结果为真(赋为1),否则输出结果为假(赋值为0)。
图8-17为一布尔逻辑“与”运算。
输入栅格1 输入栅格2 输出栅格
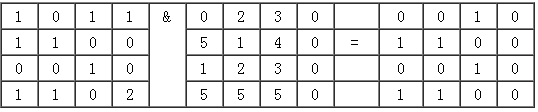
图 8.17 布尔逻辑“与”运算#
6.栅格关系运算
关系运算以一定的关系为基础,符合条件的为真,赋予1值;不符合条件的为假,赋予0值。 关系运算符包括六种:=、<、>、<>、>=和<=。
图8-18为一关系“>”运算。
输入栅格1 输入栅格2 输出栅格
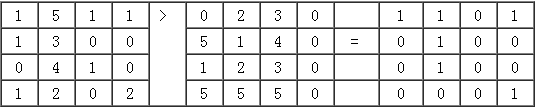
图 8.18 关系“>”运算#
矢量系统的叠加分析(拓扑叠加)#
矢量系统的叠加分析比栅格系统要复杂得多。 拓扑叠加之前,假设每一层都是平面增
强的(已经建立了完整的拓扑关系),当两层数据叠加时,结果也必然应是平面增强的。 当两线交叉时,要计算新的交叉点,一条线穿过某一区域时,必然产生两个子区域。
拓扑叠加能够把输入特征的属性合并到一起,实现特征属性在空间上的连接,拓扑叠加时, 新的组合图的关系将被更新。
叠加可以是多边形对多边形的叠加(生成多边形数据层), 也可以是线对多边形的叠加(生成线数据层)、点对多边形的叠加(生成点数据层)、多边形对点的叠加(生成多边形数据层), 点对线的叠加(生成点数据层)。 我们首先详细分析一下多边形与多边形的叠加。
1.多边形与多边形叠加
多边形与多边形合成叠加的结果,是在新的叠置图上,产生了许多新的多边形, 每个多边形内都具有两种以上的属性。 这种叠加特别能满足建立模型的需要。 例如,将一个描述地域边界的多边形数据层叠加到一个描述土壤类别分界线的多边形要素层上, 得到的新的多边形要素层就可以用来显示一个城市中不同分区的土壤类别。
由于两个多边形叠加时其边界在相交处分开,因此,输出多边形的数目可能大于输入多边形的总和。 在多边形叠加操作中往往产生许多较小的多边形,其中有些并不代表实际的空间变化, 这些小而无用的多边形称为碎多边形或伪多边形,它们是多边形叠加的主要问题,见图8-19。

图 8.19 叠加a)和b)会产生很多小的无意义的多边形-碎片c),去除碎片后为d)#
伪多边形的产生原因是同一根线在两次输入的细微差异。 如果同一条线在两张图上,数字化时必然有微小的差异,而且在大多数情况下, 图上的线是根据不同来源的数据编辑而成,编辑时常常忽略它们是同一根线的事实(例如,道路可能是县界的一部分, 同时也是两块地、两类土壤或植被的分界线)。 即使数字化时尽量增加精度,也不能消除这一现象。 有些系统允许用户设置一容差值,以消除叠加过程中产生的伪多边形,但这一容差值较难把握,因为容差过大, 有些真实的多边形被删除; 容差太小,又不能完全剔除错误的多边形。
多边形叠加的整个过程为(Tor Bernhardsen,2002):
(1)计算交叉点。
(2)形成结点和链。
(3)建立拓扑和新对象/新标识符。
(4)如果需要的话,去除大量的碎多边形,融合相似多边形。
(5)连接新属性,并添加到属性表中。
多边形叠加是一个很耗时的处理过程。 多边形叠加可以用来对数据进行一定地理区域的裁剪。 例如,用一个专题图层中的乡镇边界去叠加所有其他的专题图层,从而只得到与该乡镇相关的所有数据。
多边形与多边形的叠加可以有合并(UNION)、相交(INTERSECT)、相减(SUBSTRACTION)、判别(IDENTITY)等方式。 它们的区别在于输出数据层中的要素不同。 合并保留两个输入数据层中所有多边形; 相交则保留公共区域; 相减从一个数据层中剔除另一个数据层中的全部区域; 判别是将一个层作为模板,而将另一个输入层叠加在它上面,落在模板层边界范围内的要素被保留, 而落在模板层边界范围以外的要素都被剪切掉。
以下以图解方式详细解释几类叠加方式的不同,在以下各图中,叠加结果用阴影表示,叠加结果的属性为:
标志码、面积、周长,f1、区号、f2
其中区号为第二个数据层的区号。

图 8.20 多边形合并叠加#


图 8.21 多边形相交叠加#


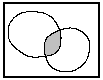

图 8.22 多边形相减叠加#


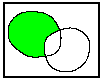


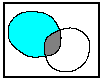

图 8.23 多边形判别叠加#
2.线对多边形叠加
线对多边形叠加的结果是一些弧段,这些弧段也具有它们所在的多边形的属性。 例如,公路以线的形式作为一层,将它与另一层的县界多边形作叠加, 其结果能够用来决定每条公路落在不同县内的公里长度。 线对多边形叠加可以有相交、判别、相减等方式, 叠加结果分别是穿过多边形的线要素部分、所有线要素(被多边形切断)、多边形以外的线要素。
3.点对多边形叠加
点对多边形叠加实质是计算包含关系,叠加结果是一串带有附加属性的点要素, 点所在的多边形的属性被连接到点的属性中。 例如,井的位置以点要素的形式作为一层土地租用分区以多边形要素的形式记录在另一层, 那么这两层作点对多边形叠加的结果可以用来确定井在各土地租用区内的分布。 点对多边形叠加也可以有相交、判别、相减等方式, 叠加结果分别是落在多边形内的点要素、所有点要素、多边形以外的点要素。
4.多边形对点叠加
多边形对点叠加的结果是多边形,但只保留那些有点落在上面的多边形,这种叠加不作属性连接, 结果多边形的属性和原始多边形相同。
5.点对线叠加
点对线叠加的结果为点要素,它保留所有点,找到距离某点最近的线并计算出点线之间的距离, 然后将线号和点线距离记录到该点的属性中。
点线距离定义如下:
对任意点D和曲线L,假设L由n个离散点d[0]、d[1]、d[2]…d[n]构成, 则D到d[0]、d[1]…d[n]的距离分别为S0、S1…Sn,D到直线段(d[0], d[1])、(d[1],d[2])…(d[n-1],d[n])的法线距离分别为:
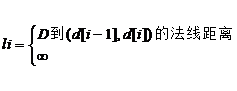

那么点D到曲线L的距离S=min(S0,S1,S2……Sn,l1,l2…ln)。
这种点对线的叠加的作用是显而易见的。 例如,建筑物以点要素形式作为一层,道路以线要素形式作为一层, 点对线的叠加将求出离每个建筑物最近的道路及相应的距离。