5.5. 图形变换#
对于输入计算机中的图形数据,有时因为比例尺不符,或为了实现地图的合成与排版, 需要对这些图形数据进行几何变换(线性变换),可满足地理信息系统应用的要求。 此外,地理信息系统所要表达、管理以及分析的对象是空间实体, 为了能在二维空间(屏幕或绘图仪)上表示三维物体,就需进行三维空间到二维空间的变换, 这种变换称为投影变换。
几何变换#
1.二维几何变换
二维几何变换包括平移、比例和旋转变换。 我们假设变换前和变换后的图形坐标分别用(x、y)和(x′、y′)表示。
平移、比例和旋转变换
平移变换:如图5-13(a)所示,它使图形移动位置。 新图p′的每一图元点是原图形p中每个图元点在x和y方向分别移动Tx和Ty产生, 所以对应点之间的坐标值满足关系式(5-6)。
x′ = x + T\ :sub:`x` 和 y′ = y + T\ :sub:`y`\
公式5-6)
可利用矩阵形式表示成公式(5-7)。
[x′ y′]=[x y]+[T\ :sub:`x` T\ :sub:`y`\ ]
(公式5-7)
简记为P′ = P + T, T =[Tx Ty]是平移变换矩阵(行向量)。
比例变换:如图5-13(b)所示,它改变显示图形的比例。 新图形p′的每个图元点的坐标值是原图形p中每个图元点的坐标值分别乘以比例常数Sx和Sy, 所以对应点之间的坐标值满足关系式(5-8)
x′ = x · S\ :sub:`x` 和 y′ = y · S\ :sub:`y`\
(公式5-8)
(公式5-9)
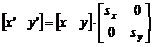
可利用矩阵形式表示成公式(5-9)。
简记成p′=P·S,其中S是比例变换矩阵。
旋转变换:图形相对坐标原点的旋转如图5-13(c)所示,它产生图形位置和方向的变动。 新图形P′的每个图元点是原图形P每个图元点保持离坐标原点距离不变并绕原点旋转θ角产生的, 以逆时针方向旋转为正角度,对应图元点的坐标值满足关系式(5-10)。
x′=xcosθ-ysinθ 和 y′=xsinθ+ycosθ
(公式5-10)
(公式5-11)
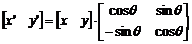
用矩阵形式表示成公式(5-11)。
简记为P′=P·R,其中R是旋转变换矩阵。
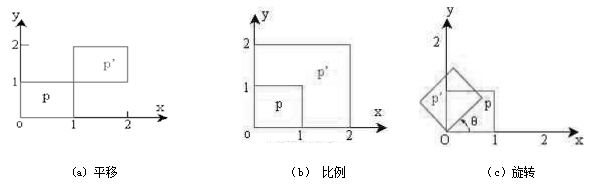
图 5.10 三种基本图形变换#
齐次坐标系
在上述三种变换中,比例和旋转变换都是作矩阵乘法。 如果这样的变换进行组合,例如旋转变换后再作比例变换,我们可得P″=P′·S=(P·R)S。 按照矩阵乘法的性质,我们可得(P·R)·S=P·(R·S),其中(R·S)构成组合变换矩阵。 若许多图形进行相同的变换,则利用组合变换可减少运算量。 但是平移变换却有形式P′=P+T,如果也能够采用矩阵的相乘形式,则三种变换便能利用矩阵乘法任意组合了。
采用几何学中的齐次坐标系可达到此目的。 即n维空间中的物体可用n+1维齐次坐标空间来表示。 例如二维空间直线ax+by+c=0,在齐次空间成为aX+bY+cW=0,以X、Y和W为三维变量, 构成没有常数项的三维平面(固此得名齐次空间)。 点P(x、y)在齐次坐标系中用P(wx,wy,w)表示,其中W是不为零的比例系数。 所以从n维的通常空间到n+1维的齐次空间变换是一到多的变换,而其反变换是多到一的变换。 例如齐次空间点P(X、Y、W)对应的笛卡尔坐标是x=X/W和y=Y/W。 将通常笛卡尔坐标用齐次坐标表示时,W的值取1。 齐次坐标系中的基本二维几何变换可表示成:
(公式5-12)
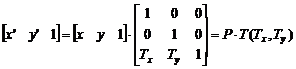
平移变换见公式(5-12)。
(公式5-13)
比例变换见公式(5-13)。
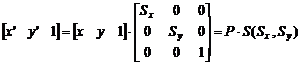
(公式5-14)
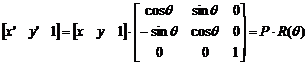
绕坐标原点旋转变换见公式(5-14)。
变换的组合
在齐次坐标中三种基本变换都用矩阵乘法表示,从而可以通过基本变换矩阵的连乘来实现变换组合, 以达到特殊变换的目的。 例如,将图形绕任意点A(xr,yr)进行旋转变换。 该变换可分成三个步骤来实现:利用平移变换T1(-Xr,-Yr)移动图形,使点(Xr, Yr)移至坐标原点; 利用旋转变换R(θ)产生绕在坐标原点的A点的旋转; 再利用平移变换T2(Xr,Yr)移动旋转后的图形,使A点回到(Xr,Yr)处。 完成全部变换的图形坐标可以表示成公式(5-15)。
(公式5-15)
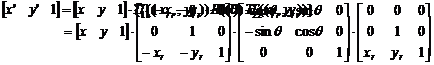
(公式5-16)
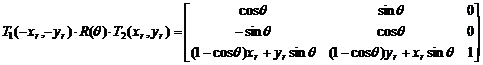
所以绕点(Xr,Yr)旋转θ角的复合变换矩阵是公式(5-16)。
任意矩阵的乘法满足结合律不满足交换律,在进行连续变换时一定要按变换次序对变矩阵求积后才得总的变换矩阵。 这和在图形变换中不同次序的变换会产生不同的变换结果相一致。 请读者自行验证。
2.三维几何变换
基本的三维几何变换也是平移、比例和旋转。 平移和比例变换是二维情况的直接推广。
(公式5-17)
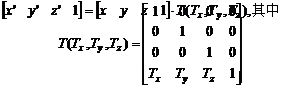
平移变换公式见(5-17)。
(公式5-18)
比例变换公式见(5-18)。

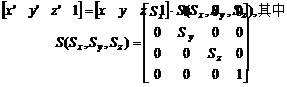
旋转变换:三维坐标系中绕过坐标原点的任意方向直线的旋转可由绕三个坐标轴的旋转组合构成。 我们规定旋转正方向与坐标轴矢量符合右手法则,即从坐标轴正值点向坐标原点观察,逆时针方向转动的角度为正。 旋转方向的定义如图5-14所示。
绕Z轴的旋转不改变原空间点的Z坐标 y
 值,它类似在二维情况中讨论过的旋转变换,
值,它类似在二维情况中讨论过的旋转变换,
(公式5-19)
因此绕Z轴旋转的坐标变换关系是(5-19)。 由坐标轴的对称性,绕x轴的旋转不改变空间点的x坐标值,绕y轴的旋转不改变y坐标值。 因此绕x轴旋转的坐标变换关系和绕y轴旋转的坐标变换关系是(5-20)和(5-21)。
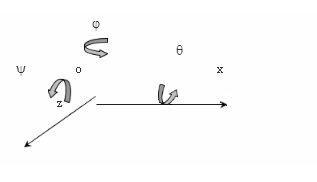
旋转方向的定义
(公式5-20)
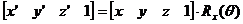
(公式5-21)
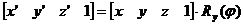
其中,
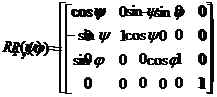
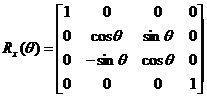
投影变换#
实际物体都是三维的,可以在三维直角坐标系中描述,但显示屏是二维的,所以最终还是用二维图形基元产生图形。 从三维物体模型描述到二维图形描述的转换过程称为投影变换。 确切地说,从空间选定的一个投影中心和物体上每点连直线便构成了一簇射线, 射线与选定的投影平面的交点集便是物体的投影。
投影变换分类见图5-15。

图 5.11 投影变换分类#
平行投影与透视投影间的区别在于投影射线是相互平行还是汇聚于一点, 或说投影中心是在无限远处还是在有限远处(见图5-16和5-17), 正平行投影与斜平行投影的区别在于投影线是否与投影平面垂直。
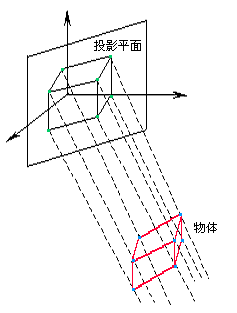
图 5.12 平行投影#
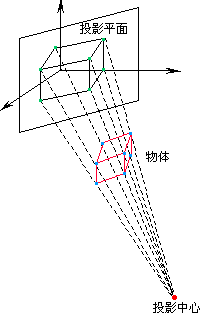
图 5.13 透视投影#
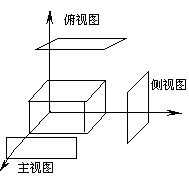
图 5.14 正投影的三视图#
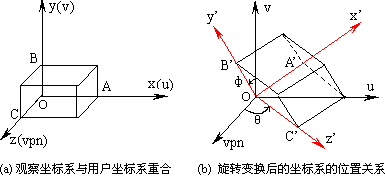
图 5.15 正轴测投影示意图(物体旋转两次,可观察到物体的三个面)#
平行投影图是物体向投影平面做平行投影所产生的图形。 例如在机械制图中的三视图就是三维向二维作特殊的平行投影-正投影的结果(见图5-18)。 这种投影实感性较差,这是因为在一个视图上只能表现物体的两个方向的情况。 如果改变投影面体系中物体的位置,或者是物体不变而选择另一个投影方向, 使在一个图中同时出现物体三个方向的情形,那么,投影图的实感性便会显著增强, 如正轴测投影和斜平行投影(见图5-19)。
透视投影属于中心投影,它比轴测投影更富有立体感和真实感,因为它能正确的表现出远近和层次关系, 使观察者获得立体的、有深度的空间感觉。