8.8. 地理信息系统的数学模型#
利用计算机解决地理信息系统中的各种实际问题时,最重要的工作是建立地理系统的数学模型, 并使建立的模型能较好地模拟实际事物的属性和规律。 正如一张地形图上,如果漏绘了一些道路,或者标错了某些山顶的高程,将会给部队指挥和行军作战造成严重后果, 说明这张地形图(也可称为符号模型)错误地描述了实际事物。 对于数学模型来说,除了具有物理模拟的特征外,还需要具有数学方法的抽象模拟, 利用数学符号、数学式子、程序等刻画实际事物的客观本质属性及其内在联系规律。 本章首先介绍建立数学模型的一般过程,然后介绍常见的数理统计模型、回归分析模型和线性规划模型。
建立数学模型的一般过程#
面对着复杂的现实世界,各种事物都处在不断的变化之中,要用数学方法去描述和模拟某些发展中的现象, 不可能采用统一的模式来论述建模问题。 但是,可以把建模过程大致划分下列几个步骤:
1.了解建模对象的实际背景,在此基础上提出建模目标
在调查研究过程中,尽可能掌握与建模有关的数据和资料。 应当访问建模对象所在领域的专家,认真总结他们在科学研究中的思路和方法以及解决问题的推理判断过程。 这些专家的逻辑思维经验是十分可贵的第一手建模材料,甚至有些经验已经构成了物理模拟的框架, 这些都是建立数学模型的基础。
2.分解模拟对象
抓住主要问题分解模拟对象,提出可能性较大的几种假设,尽可能使问题简化,减少考虑的因素。 这一过程就是数学抽象和思维的过程。 建模者应当具备这种抽象、假设能力,同时需要与该领域的专家共同讨论,使假设的现实性增加, 避免一些不必要的建模工作的重复过程。
3.数据处理
通过实地调查或测量,采集必要的数据,输入计算机,建立数据库。
4.图形显示,曲线拟合
利用某些绘图软件或采用统计回归分析的方法,调用已知数据,作出曲线图,用已知曲线拟合实际曲线。
5.模型建立
简化实际问题,提出恰当的假设,并利用适当的数学工具,刻划变量之间的关系,建立相应的数学模型, 并求得相应的解。
6.模型的验证
将模型运算结果与实际情况相比较,也就是进行误差分析,确定模型的可信程度。 如果计算结果与事实不相符合,说明在建模的过程中,可能忽略了某些重要的因素,缺乏关键的数据。 这时,必须加强对实际问题的调研,重新开始建模过程。
7.预测和决策
一个成功的地理信息系统的数学模型,不仅能解释系统的已知现象,而且还可以预测系统的某些未知现象, 把已知数据代入模型内,预测系统的发展趋势,并为系统的合理利用与开发,提供最优决策。
数理统计分析模型#
数理统计分析主要用于数据分类和综合评价,数据的分类和评价的问题通常涉及大量的相互关联的地理因素。 主成分分析方法可以从统计意义上将各影响要素的信息压缩到若干合成因子上,从而使模型大大地简化。 因子权重的确定是建立评价模型的重要步骤,权重正确与否极大地影响评价模型的正确性, 而通常的因子权重的确定依赖较多的主观判断。 层次分析法是综合众人意见,科学地确定各影响因子权重的简单而有效的数学手段。 隶属度反映因子内各类别对评价目标的不同影响,依据不同因子内的变化情况确定, 常采用分段线性函数或其它高次函数形式计算。 常用的分类和综合的方法包括聚类分析和判别分析两大类。 聚类分析可根据地理实体之间影响要素的相似程度,采用某种与权重和隶属度有关的距离指标, 将评价区域划分若干类别;判别分析类似于遥感图像处理的分类方法,即根据各要素的权重和隶属度, 采用一定的评价标准将各地理实体判归最可能的评价等级或以某个数据值所示的等级序列上。 分类定级是评价的最后一步,将模糊聚类的结果根据实际情况进行合并,并确定合并后每一类的评价等级, 对于模糊判别分析的结果序列采用等间距或不等间距的标准划分为最后的评价等级。
下面简要介绍分类评价中常用的几种数学方法。
1.主成分分析
在地理问题中,指标越多,问题分析就越复杂,但实际的指标并不一定都是独立无关的,恰恰相反, 许多指标之间存在着相当好的相关性。 因此,力求用较少的指标来进行分析研究,并要求指标同样能反映原有较多指标的信息。 找出较少指标就是要找出少数几个独立无关的变量,这种方法称之为主成分分析。
设有n个样本,p个变量。 将原始数据转换成一组新的特征值——主成分,主成分是原变量的线性组合且具有正交特征。 即将x1,x2,…, xp综合成m(m<p)个指标z1,z2, …,zm。 即
z1=l11*x1+l12*x2+…+l1p*xp
z2=l21*x1+l22*x2+…+l2p*xp (公式8-23)
………
zm=lm1*x1+lm2*x2+…+lmp*xp
这样决定的综合指标z1,z2,…, zm 分别称做原指标的第一,第二,…,第m主成分。 其中z1在总方差中占的比例最大,其余主成分z2, z3,…,zm的方差依次递减。 在实际工作中常挑选前几个方差比例最大的主成分,这样既减少了指标的数目,又抓住了主要矛盾, 简化了指标之间的关系。
从几何上看,找主成分的问题,就是找p维空间中椭球体的主轴问题, 从数学上容易得到它们是x1,x2,…, xp的相关矩阵中m个较大特征值所对应的特征向量, 通常可用雅可比法(Jacobi)计算特征值和特征向量。
显然,主成分分析这一数据分析技术是把数据减少到易于管理的程度,也是将复杂数据变成简单类别, 便于存储和管理的有力工具。 地理研究的GIS用户常使用上述技术,因而应把这些变换函数作为GIS的组成部分。
2.层次分析法
过去研究自然或社会现象主要有机理分析和统计分析两种方法。 前者用经典的数学工具分析现象的因果关系,后者以随机数学为工具,通过大量的观测数据寻求统计规律。 近年来发展起来的第三种方法称系统分析。 层次分析(AHP)法就是系统分析的数学工具之一,它把人的思维过程层次化、数量化, 并用数学方法为分析、决策预报或控制提供定量的数据。 事实上这是一种定性和定量分析相结合的方法。 在模型涉及大量相互关联、相互制约的复杂因素的情况下,各因素对问题的分析有着不同的重要性, 决定它们对目标重要性的序列,对建立模型十分重要。 AHP方法把相互关联的要素按隶属关系分为若干层次,请有经验的专家对各层次各因素的相对重要性综合定量指标,利用数学方法综合专家意见给出各层次各要素的相互重要性权值,作为综合分析的基础。 例如要比较n个因素y=|y1,y2,…, yn|对目标z的影响,确定它们在z中的比重, 每次取两个因素yi和yj, 用aij表示yi与yj对z的影响之比, 全部比较结果可用矩阵A=(aij)n×n表示, A叫做成对比矩阵,它应满足:
a\ :sub:`ij` >0,a\ :sub:`ji`\ =1/a\ :sub:`ij`\ (i,j=1,2,…,n)
(公式8-24)
使上式成立的矩阵称互反阵,不难看出必有aij=1。
在旅游问题中,假设某人考虑五个因素: 费用y1、景色y2、居住条件y3、饮食条件y4、旅途条件y5。 用成对比较法得到正互反阵是:
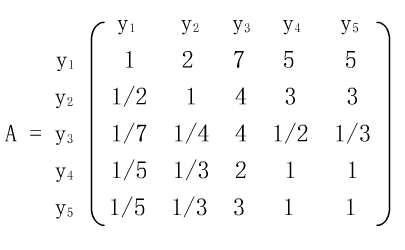
在(8-2-3)式中a12=2表示y1与景色y2对选择旅游点(目标z)的重要性之比为2:1, a13=7表示费用y1与居住条件y3之比为4∶1。 如果A不是一致阵(即A12、A23不等于A13), 需求正互反阵最大特征值对应的特征问题,作为权向量。
3.系统聚类分析
虽然数据整理能将大量而复杂的多变量数据适当压缩,但人们希望进一步减少数据的复杂程度, 即将数据定义成一组多变量类别。 主成分分析仅仅是数据沿着一条新轴的旋转和投影,得到新值,既大大压缩了原始数据也可以作为新变量使用。 主成分分析后的主分量不是按地理空间制图,而是按主成分轴定义的空间制图。 当数据在主成分空间的两坐标轴上的分布具有相似性时, 这种散射图(常把主成分空间绘制的图称散射图)能够显示出明显的类别特性即聚类特性。 如果这些聚类能归纳为分类系统中的某一类的话,就有可能进一步减少数据的复杂性。 另外,这些聚类完全由原始数据的分析推演而得,因而能代表“天然”类别, 比外生分类(按所研究数组的门槛确定其区间, 而不是由数组本身派生出来的区间)和层次分类等人为强加的类别更加真实。
60年代末到70年代初人们把大量精力集中于发展和应用数学分类法,且将这类方法应用于自然资源、土壤剖面、气候分类、环境生态等数据,形成“数学分类学”学科。 目前聚类分析已成为标准的分类技术,在许多大型计算机中都存储了这种分析程序, 从GIS数据库中将点数据传送到聚类分析程序也不困难。
聚类分析的主要依据是把相似的样本归为一类,而把差异大的样本区别开来。 在由m个变量组成的m维的空间中,可以用多种方法定义样本之间的相似性和差异性统计量。 它是一种定量方法,从数学分析的角度,给出一个更准确、细致的分类。
(公式8-26)
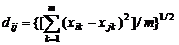
用xik表示第i个样本第k个指标的数据, xjk表示第j个样本第k个指标数据。 Dij表示第i个样本和第j个样本之间的距离,根据不同的需要,距离可以定义为许多类型,最常见、最直观的距离是欧氏(Euclid)距离,其定义如下:

依次求出任何两个点的距离系数 dij
(i,j=1,2,…,n)以后,即可形成一个距离矩阵:
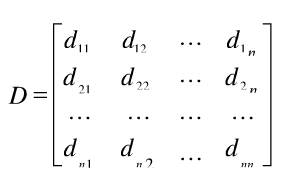
(公式8-27)
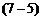
它反映了地理单元的差异情况,在此基础上就可以根据最短距离法或最大距离法或中位线法等进行逐步归类, 最后形成一张聚类分析谱系图,如图8-42。
 除上述的欧氏距离外,定义相似程度的还有绝对值距离、切比雪夫距离、马氏距离、兰氏距离、相似系数和定性指标的距离等。
除上述的欧氏距离外,定义相似程度的还有绝对值距离、切比雪夫距离、马氏距离、兰氏距离、相似系数和定性指标的距离等。
4.判别分析
判别分析的特点是根据已掌握的、历史上每个类别的若干样本的数据信息,总结出客观事物分类的规律性, 建立判别公式和判别准则,就能判别该样本所属的类别。 例如,在评价产品的市场竞争力时, 可根据商品的多项指标(诸如其内在质量、外型美观以及包装、价格等)判别消费者对商品喜欢或判别分析依其判别类型的多少与方法的不同, 可分为两总体判别、多总体判别和逐步判别等。 判别分析要求根据已知的特征值进行线性组合,构成一个线性判别函数y,
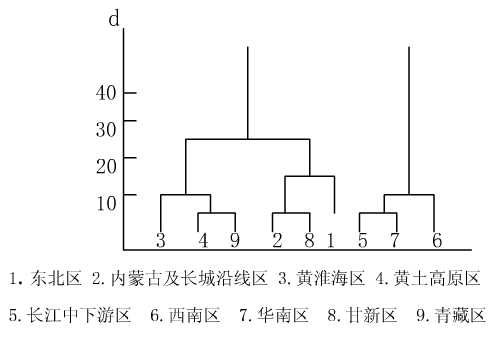
图 8.41 九大农业区聚类谱系图#
(公式8-28)
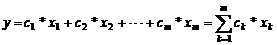
(公式8-29)
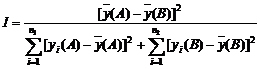
式中,ck(k=1,2,…,m)为判别函数, 它可反映各要素或特征值作用方向、分辨能力和贡献率的大小。 只要确定了ck,判别函数y也就确定了。 xk为已知各要素(变量)的特征值。 为了使判别函数y能充分地反映出A、B两种类型的差别, 就要使用两类之间均值差[y(A)-y(B)]2尽可能大, 而各类内部的离差平方和尽可能小。 只有这样,其比值I才能达到最大,从而能将两类清楚地分开。 其表达式为:
判别函数求出以后,还需要计算出判别临界值,然后进行归类。 不难看出,经过二级判别所作的分类是符合区内差异小而区际差异大的划区分类原则的。
回归分析模型#
回归分析是研究因变量y和自变量x之间存在某种相关关系的方法, 其中要求自变量x是可以控制或可以精确观察的变量,因此当x取每一个确定值后,y就有一定的概率分布。 若y的数学期望存在,则其值是x的函数。 即y=μ(x),这个μ(x)称为y对x的回归函数,或称y关于x的回归。 回归函数可以是一元函数,也可以是多元函数,可以是线性的,也可以是非线性的。 下面我们主要介绍一元线性回归和多元线性回归模型。
1.一元线性回归横型
假设自变量为x,因变量为y,估计y与x之间存在线性关系,则有
- y=β0+β1x
(公式8-30)
其中β0,β1是待定的未知常数,称为回归系数。 式(8-3-1)称为一元线性回归模型。 设(xi,yi)i=1,2,…,n是一组观测数据, 考虑到实际观测中,由于随机因素的干扰,因变量的取值不仅与自变量的取值有关,而且与误差有关, 我们利用这组数据, 建立如下方程组:yi=β0+β1xi+eii=1, 2,…,n (公式8-31)
ei表示观测过程中随机因素对yi的影响误差,假设ei是独立同分布的不可观测的随机变量,ei~N(0,σ2)。 yi是可观测的(即能给出样本值的)独立的随机变量,yi~N(β0+β1xi,σ2)。 xi可以是一般变量,也可以是随机变量。
(8-31)式中的回归系数β0与β1,随机误差ei通过以下方法估计其值。 将β0与β1的估计值代入(8-30)式用来确定x与y之间的对应关系, 利用ei的估计值可以评价模型的有效性。
通常是采用最小二乘法估计β0与β1。 其原理是选取β0, β1的估计量β0与β1, 使误差ei的平方和达到最小。 令
(公式8-32)
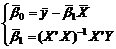
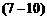
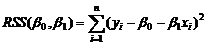
RSS(β0,β1)是残差的平方和。 利用拉格朗日乘子法,易从上式中求出:
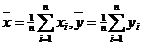
这里x=(x1,x2,…,xn)′, y=(y1,y2,…,yn)′
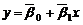
(公式8-33)


把(8-32)式解得的β0,β1代入(8-31)式,则有
称为n个观测点上的回归预报值。
然而,变量x,y之间是否存在线性关系?假若y不依赖于x,即当x变化时,y总是一确定的值, 那么y与x之间也就不存在线性关系。 因此,需要进行假设检验。 现采用平方和分解方法,实行假设检验。 令
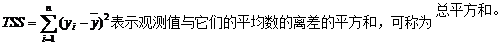

它们之间存在如下的数量关系:
TSS=ESS+RSS(公式8-34)
这个等式说明,y的观测值的总平方和可分解为两部分:
(公式8-35)
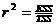
一部分可归于回归方程存在的原因,另一部分则是随机因素所致。 这样,就可以如下定义系数:
显然0≤r2<1,通常把r称为相关系数。 r2越接近于零,x,y之间线性相关的程度越小;反之,r2越接近于1,x,y之间线性相关程度越密切。 故只有当r2大到一定程度时,相关性才是显著的。 相关性显著的指标采用F统计量来衡量。
设: fTSS:总平方和的自由度;|
fTSS=总观测数-1=n-1|
fESS:回归平方和的自由度;|
fESS=回归系数的个数-1,对于一元线性回归模型:|
fESS=1|
fRSS:残差平方和的自由度;|
fRSS=总观测数-回归系数的个数=n-2
(公式8-36)
平方和除以相应的自由度,称为均方。 可以证明:残差平方和的均方是误差方差σ2的一个无偏估计。 令:
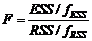
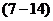
将fESS=1,fRSS=n-2,代入公式(8-36), 有:
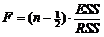
在给定分子和分母的自由度,以及显著水平α,可以从F分布的统计表中查出F值,记住Fα, 将式(8-3-7)所得的F值与Fα相比较,当F>Fα时, 则认为对于给出的α水平,相关性是显著的; 反之,若F<Fα,则认为相关性是不显著的,y与x之间用线性描述。
2.多元线性回归模型
设自变量x1,x2,…, xm与因变量y有关,这时需采用多元线性回归模型。
(公式8-37)
y=β0+β1x1+β2x2+…+βmxm (7-15)
假设yi,xi1,xi2,…, xim(i=1,2,…,n)是n次观测数据,它们之间有如下关系:
yi=β0+β1xi1+β2xi2+…+βmxim+ui(i=1,2,…,n)
(公式8-38)
式中:β0—截距;|
β1,β2,…,β—偏回归系数;|
ui—随机干扰项;|
i—第i个观测值;|
n—总体容量。
为将(8-38)式改写为矩阵形式,令
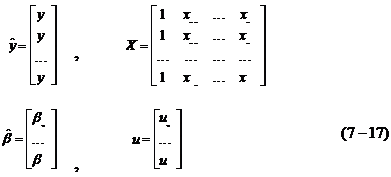

(公式8-39)
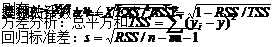
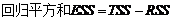
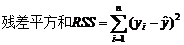
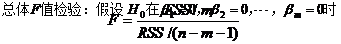
当F值大于临界值时,拒绝H0,即认为线性回归方程显著。
回归系数t检验:对于i=0,1,…,m。 H0在β1=0,β2=0,…,βm=0时
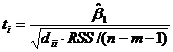
其中 dii=( XTX )-1, ti大于临界值时,拒绝 H0, 即认为 βi是相关显著的。
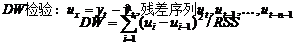
设临界值上、下限为du,dl,则
du<DW<4-du无自相关
dl<DW<du和4-du<DW<4-dl
不能确定
DW<dl 正自相关
DW>4-dl 负自相关
当残差序列自相关性较弱时,DW=2 。
3.计算实例
在表8-1数据基础上计算出回归方程。
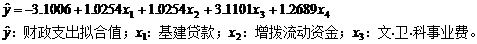
x4:其它费用。
复相关系数 r=0.9989
回归标准差 s=15.6855
F值检验=3112.011
DW值检验 DW=1.43065
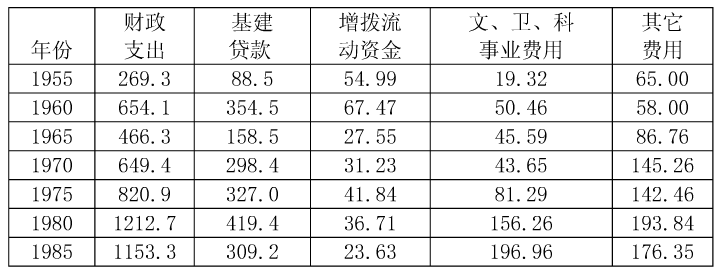
图 8.42 实例数据#
t检验值t1=0.3479,t2=20.6079,t3=5.1533,t4=29.1832,t5=10.7656
从回归结果看,这个模型的拟合情况是较好的。
线性规划模型#
线性规划的一般数学模型如下:|
(公式8-40)
(公式8-42)
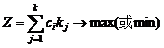
目标函数:
(公式8-41)
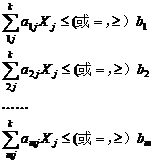
限制条件:
(8-43)
式中:cj(j=1,2,…,k)代表价格系数、费用系数或利润系数;
aij(i=1,2,…,m;j=1,2,…,k)代表已知常数,或叫做资源消耗系数;
bi(i=1,2,…,m)代表资源数量;
xj(j=1,2,…,k)代表所求的未知数。
下面将利用线性规划模型,以山东省禹城旱涝碱综合治理实验区为例论证该区农作物结构远景的最优方案。 目标是使粮食、棉花、油料和麻类四种作物(占该区总耕地的绝大部分)的产值达到最大。 设粮、棉、油、麻四种作物的面积占耕地总面积(或这几种作物的面积占总耕地面积之和)的比例分别为x1、x2、x3、x4。 预测这四种作物的亩产分别达到400公斤、50公斤、100公斤、200公斤, 每公斤的价格分别为0.2572元、2.956元、0.9478元、2.077元。 于是便可写出一个求亩产值达到最大的目标函数:
Z=0.2572×400x1+2.956×50x2+0.9478×100x3+2.077×200x4→max
为了达到这个目标,必须充分利用当地自然、经济优势,有效利用土地和水、肥、劳力等资源, 并按一定数量指标建立一系列关系式。
设耕地面积等于1,则四种作物占用耕地的约束可写成:
x1+x2+x3+x4≤1
经过估算,该区粮、棉、油、麻四种作物每亩耗水量分别为190方、140方、117方、100方。 每亩平均耗水量不超过170方,于是便有:
190x1+140x2+117x3+100x4≤170
按估测,以上四种作物每亩平均化肥施用量分别为50公斤、80公斤、64公斤、26.5公斤, 每亩平均不超过55公斤。 则施肥水平限制可写成:
50x1+80x2+64x3+26.5x4≤55
经过估算,以上四种作物每亩平均用工分别为35个、50个、30个、28个。 平均不超过37个,则劳动力限制可写成:
35x1+50x2+30x3+28x4≤37
根据国家需要,粮食耕地占总耕地的比重不能小于0.65,由于市场和销路的限制, 麻类种植占耕地比重不能大于0.08。 于是就有:
x1≥0.65
x4≤0.08
归纳以上分析的全部情况,便获得了一个完整的农作物结构线性规划模型:
目标函数: Z=102.9x1+148.8x2+94.8x3+415.4x4→max
约束条件:190x1+140x2+117x3+100x4≤170
50x1+80x2+64x3+26.5x4≤55
35x1+50x2+30x3+28x4≤37
x1+x2+x3+x4≤1.0
x1≥0.65
x4≤0.08
其中x1,x2,x3, x4≥0
求目标函数Z和变量x1,x2, x3和x4的最优解。
为解决这一问题,利用了线性规划单纯型法求解程序,通过计算机运算从而求出最优解。 其结果见表8-2。

图 8.43 程序的结果#
为了检验各约束条件在实现最优解中的作用,还进行了灵敏度分析。 灵敏度是指目标函数的最优解,对于约束条件的单位变化(这里是按约束值增加1%时计算的)反应的灵敏性度量。 若第一个约束条件值为bi, 若bi有一个变化量为Δbi而引起目标函数Z的最优值变化为ΔZ, 则灵敏度λi=ΔZ/Δbi。 表8-3给出灵敏度分析结果。

图 8.44 灵敏度分析的结果#
经验证明所得到的方案可行。 现将其与5年前的基数作一对比,见表8-4。
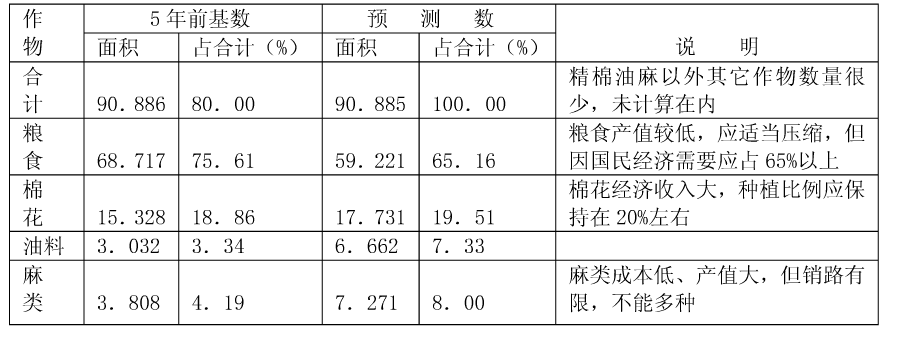
图 8.45 与5年前的基数对比#
下面再用同样方法对实验区的大农业结构的最优方案进行预测。 设农业、林业、牧业和副业(包括为数不多的渔业)占该区农业总收入的比重分别为x1, x2,x3,x4,已知条件
见表8-5。
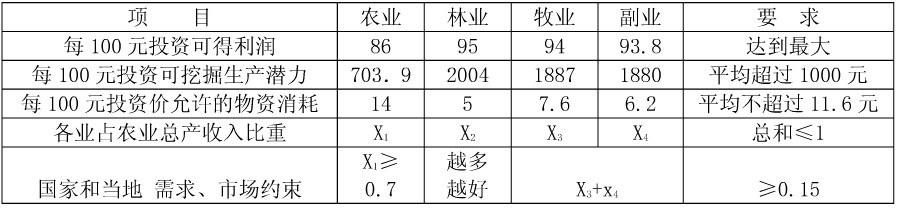
图 8.46 农业结构的已知条件#
根据上表,可以获得一个求利润最大的线性规划模型:
目标函数: Z=86x1+95x2+94x3+93.8x4→max
约束条件: 14x1+5x2+7.6x3+6.2x4≤11.6(1)
703.9x1+2004x2+1887x3+1800x4≥1000(2)
x1+x2+x3+x4≤1.0(3)
x1≥0.70(4)
x3+x4≥0.15(5)
其中x1,x2,x3, x4≥0
利用线性规划单纯形法求解程序,通过计算机运算和验证所获得的最优解结果如下: 农业(种植业)占农业总收入比重 x1=0.70
林业占农业总收入比重 x2=0.1499
牧业占农业总收入比重 x3=0.0857
副业占农业总收入比重 x4=0.0629
目标函数即每100元投资可能获得的最大利润为88.53元。