9.8. DEM 分析的误差与精度¶
DEM 已经在测绘、资源与环境、灾害防治、国防等各应用领域内发挥着越来越巨大的作用。 然而,各类 DEM 误差的存在不同程度地降低了分析与应用结果的可信度。 强化对基于地形图的 DEM 精度检查与质量评估的研究,为各类GIS分析产品提供科学合理的质量标准, 对评价 DEM 数据质量,减少生产单位质量检查的盲目性等方面有着深远的影响, 具有十分重要的理论意义和应用价值。
9.8.1. DEM 的误差研究概况¶
关于 DEM 的误差,国外己有很多研究,20世纪80年代以来,对 DEM 误差问题的研究取得了一些重要的成果。 如从不同侧面进行了DME高程采样误差的成因分析,对 DEM 误差的量化、检测方法和空间分布等进行了研究。 国内学者对于 DEM 数据精度作了深层次的研究,从不同角度探讨了 DEM 误差的成因、影响因素、 数学模拟以及对GIS空间分析应用的影响,初步建立了一套利用不同信息源建立 DEM 的技术规范。 另外,对地形描述的不确定性研究中提出区别于高程采样误差的DME地形描述误差概念, 对DME地形描述误差的形成条件、空间分布特征、数学模拟方法等一系列问题进行了系统分析, 提出了 DEM 地形描述误差在宏观与微观两个层面的数学模拟的模型。 同时,还对不同比例尺、不同栅格分辨率 DEM 的不确定性特征与转换模型进行了研究, 为有效估算 DEM 的地形描述精度及确定适宜的 DEM 分辨率提供了理论依据等等。 并且,随着技术的发展, DEM 生产自动化程度的提高,将会研发出自动化程度较高的 DEM 数据质量控制与检查软件, 以满足生产作业和数据应用中的急需。
9.8.2. DEM 的误差来源¶
DEM 误差的产生与 DEM 的生产过程密切相关, DEM 的生产一般经过原始数据的采集和内插建模两个阶段, 在此基础上,把 DEM 误差分为数据源误差和内插建模误差。 原始数据的采集误差:主要来自原始资料的误差、采点设备误差、人为误差、采集过程中产生的误差等。 内插建模误差:在建立 DEM 的过程中,由于需要经过内插计算和建模处理, 内插点的计算高程总是与实际量测高程之间存在差异,称为内插计算及建模误差。 该误差一方面与内插算法有关,另一方面也与原始数据的分布和密度有关。
9.8.3. DEM 的误差分析¶
原始数据的采集主要是利用不同的采集方式获取 DEM 原始数据的过程, 数据采集可分为直接采集方法和间接采集方法两种(牛志宏,2007)。
1.直接采集数据的误差
直接法采集数据主要包括通过GPS测量和全站仪等测量仪器直接从野外获取数据,是 DEM 数据局部更新的主要方法。 通过该方法获取的数据精度高,实时性强,但野外观测量大,需耗费大量的人力、物力。 随着实时差分(RTK)技术的出现,采用GPS获取 DEM 数据也越来越广泛。 因此,直接法采集数据的误差主要是GPS和全站仪等的观测误差。
2.间接采集数据的误差
(1)通过地图采集数据的误差。 主要包括原图误差和数字化误差。 原图误差主要包括地图制作过程中地图控制点的展绘、编绘误差、绘图误差、综合误差、地图复制误差、 分色板套合误差、图纸变形误差等。
地图数字化主要有两种方式:手扶跟踪数字化和扫描数字化。 目前采用较多的是扫描数字化方法。 扫描数字化的误差主要包括扫描图像的误差、图像定向误差和扫描处理软件对数字栅格图像处理的误差。 由于扫描数字化方式获取数据速度快、劳动强度小、自动化程度高等优点已成为获取 DEM 数据的主要手段。
(2)通过遥感图像采集数据的误差。 遥感数据获取与处理的每一个过程都会引入误差,一般分为获取遥感图像的误差、图像处理和解译误差。 获取遥感图像的误差主要表现为空间分辨率、几何畸变和辐射误差。 遥感图像处理和解译误差主要包括图像压缩、数据分析和判读分析、影像存储、影像增强、处理、量化、空间滤波, 以及影像模式识别等过程产生的误差,特别是图像压缩和数据分析和判读过程中的误差。
(3)通过摄影测量采集数据的误差。 此类误差主要可归结为像点误差与定向误差。 像点误差是在进行绝对定向前各种系统误差与偶然误差的综合误差,主要表现为获取航片误差与坐标量测误差。 定向误差包括相对定向和绝对定向的误差,相对定向误差主要取决于像点误差, 特别是同名像点量测的误差以及对像点坐标系统误差的校正程度,其定向精度可根据平差结果进行估计。 绝对定向误差主要与采用的模型、地面点的误差、分布等有关。 减弱该类误差主要是选取合适的数学模型、采用足够多的分步均匀的像控点。
3. DEM 内插建模误差
DEM 的内插是根据若干相邻参考点的高程求出待定点上的高程值,一般将其分为三类: 即整体内插、分块内插和逐点内插。 整体内插主要是通过多项式函数来实现的,它的拟合模型是由研究区域内所有采样点的观测值建立的。 分块内插是把需要建立数字高程模型的地区切割成一定尺寸的规则分块,在每一分块上展铺一张数学面。 逐点内插法是以待插点为中心,定义一个局部函数去拟合周围的数据点, 数据点的范围随待插点的位置变化而变化,如移动拟合法、加权平均法、Voronoi图法等。
9.8.4. DEM 的误差评价模型¶
DEM 精度评估可通过两种不同的方式来进行,一种是平面精度和高程精度分开评定,另一种是两种精度同时评定。 对前者,平面的精度结果可独立于垂直方向的精度结果而获得,但对后者,两种精度的获取必须同时进行。 在实际应用中,一般只讨论 DEM 的高程精度评定问题。
数字高程模型的精度评定可有三种途径:一是理论分析,二是试验检测,三是理论与试验相结合。 理论分析和理论与试验相结合方法的共同特点都是试图寻求对地表起伏复杂变化的统一量度和各种内插数学模型 的通用表达方式,使评定方法、评定所得的精度和某些带规律性的结论有比较普遍的理论意义, 所不同的是前者纯粹是理论研究,而后者要通过大量的实验来建立数学模型。 应当指出,由于影响数字高程模型的因素是多种多样的,因此无论采用哪种途径都不能很好地解决所有的问题。
在实际应用中,常用的 DEM 精度评定模型有检查点法、剖面法等。
1. DEM 精度指标
对于 DEM 精度的评估很难提出一个通用的评估标准,一般都是用中误差和最大误差来评估, 这两个指标反映了格网点的高程值不符合真值的程度。
(1)中误差,其公式是:
- sub:
(公式9-42)
- sub:
为 DEM 的中误差,n为抽样检查点数,Zk为检查点的高程真值, Rk内插出的 DEM 高程。 高程真值是一个客观存在的值,但它又是不可知的,一般把多次观测值的平均值即数学期望近似地看作真值。
中误差是内插生成的 DEM 数据格网点相对于真值的偏离程度。 这一指标被普遍运用于 DEM 的精度评估。
(2)最大误差
格网点的高程值不符合真值的最大偏离程度。
2.常用 DEM 精度评定模型
(1)检查点法
检查点法即事先将检查点按格网或任意形式进行分布,对生成的 DEM 在这些点处进行检查。 将这些点处的内插高程和实际高程逐一比较得到各个点的误差,然后算出中误差。 这种方法简单易行,是一种比较常用的方法。
(2)剖面法
剖面法是将一定的剖面量测计算高程点和实际高程点进行比较的精度计算方法。 剖面可以沿X方向、Y方向或任意方向。 可以用数学方法(如传递函数法)计算任意剖面的误差,也可以用实际剖面和内插剖面相比较的方法估算高程误差。
3. DEM 精度评定数学模型
(1)传递函数模型
主要采用通过断面的实际量测高程和拟合高程的傅立叶级数来估计误差的, 其原理是任何一个连续曲面的剖面均可表示为一个傅立叶级数:
- sub:
(公式9-43)
- sub:
(公式9-44)
式中:sub: 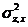 在x断面的高程误差(在y断面上和在x断面上相同);
:sub:
在x断面的高程误差(在y断面上和在x断面上相同);
:sub: 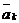 和:sub:
和:sub: 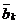 为断面实际曲线的傅立叶级数各项的系数;
ak和bk为断面内插曲线的傅立叶级数各项的系数。
采用这种方法可评价 DEM 在X方向、Y方向或任意方向断面上的高程点精度。
为断面实际曲线的傅立叶级数各项的系数;
ak和bk为断面内插曲线的傅立叶级数各项的系数。
采用这种方法可评价 DEM 在X方向、Y方向或任意方向断面上的高程点精度。
应当指出,由于影响 DEM 精度因素的多样性,在考察 DEM 的精度时,不仅要考虑 DEM 的单点误差, 还要考虑 DEM 在山区、平原地区、平缓地区和破碎地区的整体形状,使 DEM 不仅在单点的精度达到相当的水平, 而且整个 DEM 的形状和实际地形保持一致。
(2)协方差函数模型
协方差函数法可从理论上估算网格点或任意点处的高程误差。 它是将地表起伏看作一个随机函数,然后用一个协方差函数来表示地表起伏的复杂程度。 假定各参考点之间的相关性仅取决于点间的水平距离,而与点位和方向无关。 一般选用高斯函数来拟合经验的协方差函数:
- sub:
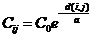 (公式9-45)
(公式9-45)
对于多项式、二元样条等数学模型,点P高程内插的方差为:
- sub:
(公式9-46)
式中,i,j=1,2,…,n,C为协方差, A为数学模型的系数矩阵。
对于多层叠加面和最小二乘配置法等数学模型,点P高程内插的方差为:
- sub:
(公式9-47)
(3)高频谱分析函数模型
Frederiksen(1980)也设计了一个基于高频部分地形断面的傅立叶谱总和的数学模型, 换句话说就是地形高于Dx/2,Dx为采样间距。 然而,该模型忽略了这样的事实,也就是随着数据采样间距的增大,频谱幅度将减小, 因此会产生过于乐观的预测结果。