scipy.stats.multivariate_normal¶

scipy.stats.multivariate_normal = <scipy.stats._multivariate.multivariate_normal_gen object>[源代码]¶

多变量正态随机变量。

这个 mean 关键字指定平均值。这个 cov 关键字指定协方差矩阵。

参数

xarray_like

分位数，最后一个轴为 x 表示组件。

meanARRAY_LIKE，可选

分布的平均值(默认为零)

covARRAY_LIKE，可选

分布的协方差矩阵(默认为1)

allow_singular布尔值，可选

是否允许使用奇异协方差矩阵。(默认值：FALSE)

random_state ：{无，整型， numpy.random.Generator ，{无，整型，

numpy.random.RandomState }，可选

如果 seed 为无(或 np.random )、 numpy.random.RandomState 使用的是Singleton。如果 seed 是一个整型、一个新的 RandomState 实例，其种子设定为 seed 。如果 seed 已经是一个 Generator 或 RandomState 实例，则使用该实例。

或者，可以调用对象(作为函数)来固定平均值

和协方差参数，返回“冻结的”多变量正态

随机变量：

rv = multivariate_normal(mean=None, cov=1, allow_singular=False)

使用相同的方法冻结对象，但保持给定的均值和协方差不变。

注意事项

设置参数 mean 至 None 相当于拥有 mean: 做零矢量。该参数 cov 可以是标量，在这种情况下，协方差矩阵是该值的单位乘以、协方差矩阵的对角条目向量或二维array_like。

协方差矩阵 cov 必须是(对称)半正定矩阵。的行列式和逆式 cov 分别作为伪行列式和伪逆计算，因此 cov 不需要拥有完整的级别。

的概率密度函数 multivariate_normal 是

\[F(X)=\frac{1}{\sqrt{(2\pi)^k\det\sigma}} \EXP\LEFT(-\FRAC{1}{2}(x-\µ)^T\Sigma^{-1}(x-\MU)\Right)，\]

哪里 \(\mu\) 是卑鄙的， \(\Sigma\) 协方差矩阵，以及 \(k\) 是空间的维度，其中 \(x\) 取值。

0.14.0 新版功能.

示例

>>> import matplotlib.pyplot as plt
>>> from scipy.stats import multivariate_normal

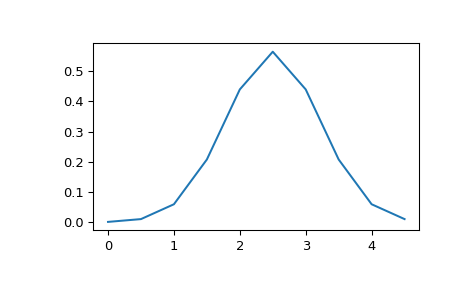
>>> x = np.linspace(0, 5, 10, endpoint=False)
>>> y = multivariate_normal.pdf(x, mean=2.5, cov=0.5); y
array([ 0.00108914,  0.01033349,  0.05946514,  0.20755375,  0.43939129,
        0.56418958,  0.43939129,  0.20755375,  0.05946514,  0.01033349])
>>> fig1 = plt.figure()
>>> ax = fig1.add_subplot(111)
>>> ax.plot(x, y)

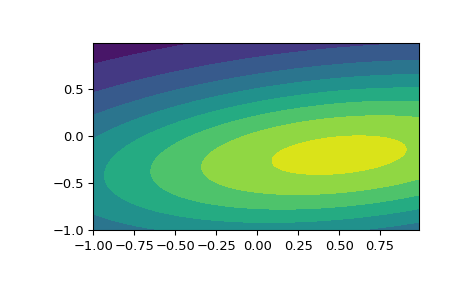
输入分位数可以是任意形状的数组，只要最后一个轴标记组件即可。这允许我们例如以如下方式以2D显示非各向同性随机变量的冻结PDF：

>>> x, y = np.mgrid[-1:1:.01, -1:1:.01]
>>> pos = np.dstack((x, y))
>>> rv = multivariate_normal([0.5, -0.2], [[2.0, 0.3], [0.3, 0.5]])
>>> fig2 = plt.figure()
>>> ax2 = fig2.add_subplot(111)
>>> ax2.contourf(x, y, rv.pdf(pos))

../../_images/scipy-stats-multivariate_normal-1_00.png

../../_images/scipy-stats-multivariate_normal-1_01.png

方法：

``pdf(x, mean=None, cov=1, allow_singular=False)``	概率密度函数。
``logpdf(x, mean=None, cov=1, allow_singular=False)``	概率密度函数的对数。
*``cdf(x, mean=None, cov=1, allow_singular=False, maxpts=1000000dim, abseps=1e-5, releps=1e-5)``**	累积分布函数。
*``logcdf(x, mean=None, cov=1, allow_singular=False, maxpts=1000000dim, abseps=1e-5, releps=1e-5)``**	累积分布函数的日志。
``rvs(mean=None, cov=1, size=1, random_state=None)``	从多元正态分布中随机抽取样本。
``entropy()``	计算多元正态分布的微分熵。

scipy.stats.wrapcauchy

scipy.stats.matrix_normal