scipy.stats.kurtosis

scipy.stats.kurtosis(a, axis=0, fisher=True, bias=True, nan_policy='propagate')

计算数据集的峰度(Fisher或Pearson)。

峰度是第四个中心矩除以方差的平方。如果使用费舍尔的定义，则从结果中减去3.0，得出正态分布的0.0。

如果偏差为假，则使用k统计量来计算峰度，以消除来自有偏矩估计器的偏差

使用 kurtosistest 看看结果是否足够接近正常。

参数

a阵列

计算峰度的数据。

axis整型或无型，可选

沿其计算峰度的轴。默认值为0。如果没有，则对整个阵列进行计算 a 。

fisher布尔值，可选

如果为True，则使用费舍尔定义(NORMAL==>0.0)。如果为False，则使用Pearson的定义(Normal==>3.0)。

bias布尔值，可选

如果为False，则会更正计算的统计偏差。

nan_policy{‘Propagate’，‘RAISE’，‘OMIT’}，可选

定义输入包含NaN时的处理方式。‘Propagate’返回NaN，‘Raise’抛出错误，‘omit’执行忽略NaN值的计算。默认值为“Propagate”。

退货

kurtosis阵列

值沿轴线的峰度。如果所有值都相等，则为费舍尔定义返回-3，为皮尔逊定义返回0。

参考文献

1

Zvelinger，D.和Kokoska，S.(2000)。CRC标准概率和统计表和公式。查普曼与霍尔：纽约。2000年。

示例

在Fisher定义下，正态分布的峰度为零。在下面的示例中，峰度接近于零，因为它是根据数据集计算的，而不是根据连续分布计算的。

>>> from scipy.stats import norm, kurtosis
>>> data = norm.rvs(size=1000, random_state=3)
>>> kurtosis(data)
-0.06928694200380558

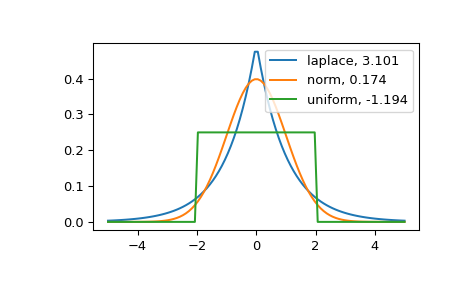
峰度高的分布有较重的尾部。Fisher定义的正态分布的零值峰度可以作为参考点。

>>> import matplotlib.pyplot as plt
>>> import scipy.stats as stats
>>> from scipy.stats import kurtosis

>>> x = np.linspace(-5, 5, 100)
>>> ax = plt.subplot()
>>> distnames = ['laplace', 'norm', 'uniform']

>>> for distname in distnames:
...     if distname == 'uniform':
...         dist = getattr(stats, distname)(loc=-2, scale=4)
...     else:
...         dist = getattr(stats, distname)
...     data = dist.rvs(size=1000)
...     kur = kurtosis(data, fisher=True)
...     y = dist.pdf(x)
...     ax.plot(x, y, label="{}, {}".format(distname, round(kur, 3)))
...     ax.legend()

拉普拉斯分布比正态分布有更重的尾部。均匀分布(峰度为负值)的尾巴最细。

上一页

scipy.stats.hmean

下一页

scipy.stats.mode