scipy.special.airy¶
- scipy.special.airy(z) = <ufunc 'airy'>¶
ALEY函数及其导数。
- 参数
- zarray_like
真实的或复杂的论点。
- 退货
- AI、AIP、Bi、Bip射线
Ay函数Ai和Bi,以及它们的导数Aip和Bip。
参见
airye指数缩放的艾里函数。
注意事项
Ary函数Ai和Bi是下式的两个独立解
\[y‘’(X)=x y(X)。\]真的 z 在……里面 [-10, 10], the computation is carried out by calling the Cephes [1]
airy例程,它使用幂级数求和 z 和有理极大极小逼近 z 。在这个范围之外,阿莫斯人 [2] ‘zairy’和 zbiry 例行公事都是用到的。它们是使用幂级数计算的 \(|z| < 1\) 以及下列与修改的Bessel函数的关系(对于较大的Bessel函数 z (其中 \(t \equiv 2 z^{{3/2}}/3\) ):
\[ \begin{align}\begin{aligned}Ai(Z)=\frac{1}{\pi\sqrt{3}}K_{1/3}(T)\\ai‘(Z)=-\frac{z}{\pi\sqrt{3}}K_{2/3}(T)\\BI(Z)=\sqrt{\frac{z}{3}}\Left(i_{-1/3}(T)+I_{1/3}(T)\right)\\Bi‘(Z)=\frac{z}{\sqrt{3}}\Left(i_{-2/3}(T)+I_{2/3}(T)\right)\end{aligned}\end{align} \]参考文献
- 1
Cphes数学函数库,http://www.netlib.org/cephes/
- 2
唐纳德·E·阿莫斯,“AMOS,一种用于复变元和非负阶贝塞尔函数的便携式软件包”,http://netlib.org/amos/
示例
区间上的Ary函数的计算 [-15, 5] 。
>>> from scipy import special >>> x = np.linspace(-15, 5, 201) >>> ai, aip, bi, bip = special.airy(x)
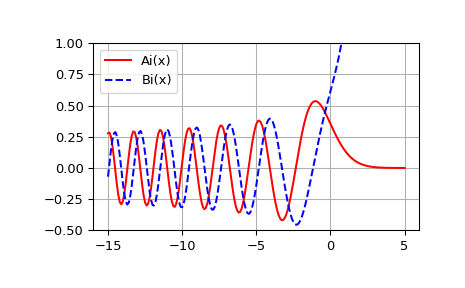
图Ai(X)和Bi(X)。
>>> import matplotlib.pyplot as plt >>> plt.plot(x, ai, 'r', label='Ai(x)') >>> plt.plot(x, bi, 'b--', label='Bi(x)') >>> plt.ylim(-0.5, 1.0) >>> plt.grid() >>> plt.legend(loc='upper left') >>> plt.show()