scipy.signal.correlate¶
- scipy.signal.correlate(in1, in2, mode='full', method='auto')[源代码]¶
使两个N维数组相互关联。
互相关 in1 和 in2 ,输出大小由 mode 论点。
- 参数
- in1array_like
第一次输入。
- in2array_like
第二个输入。应具有与的维度数量相同的维度 in1 。
- modestr{‘完整’,‘有效’,‘相同’},可选
指示输出大小的字符串:
full输出是输入的全离散线性互相关。(默认)
valid输出只包含那些不依赖于补零的元素。在“有效”模式下, in1 或 in2 必须在每个维度上至少与其他维度一样大。
same输出的大小与 in1 ,相对于“完整”输出居中。
- methodstr{‘AUTO’,‘DIRECT’,‘FFT’},可选
一个字符串,指示使用哪种方法计算相关性。
direct相关性直接从相关的定义总和中确定。
fft快速傅立叶变换用于更快地执行关联(仅适用于数字数组)。
auto根据估计的速度较快(默认)自动选择直接或傅立叶方法。看见
convolve备注了解更多详细信息。0.19.0 新版功能.
- 退货
- correlate阵列
包含以下项的离散线性互相关子集的N维数组 in1 使用 in2 。
参见
choose_conv_method包含有关以下内容的更多文档 method 。
correlation_lags计算一维互相关的滞后/位移指数数组。
注意事项
两个d维数组x和y的相关性z定义为:
z[...,k,...] = sum[..., i_l, ...] x[..., i_l,...] * conj(y[..., i_l - k,...])
这样,如果x和y是一维阵列,并且
z = correlate(x, y, 'full')然后\[Z [k] =(x*y)(k-N+1) =\SUM_{l=0}^{| |x| |-1}x_l y_{l-k+N-1}^{*}\]为 \(k = 0, 1, ..., ||x|| + ||y|| - 2\)
哪里 \(||x||\) 的长度是
x, \(N = \max(||x||,||y||)\) ,以及 \(y_m\) 当m超出y的范围时为0。method='fft'仅适用于数字数组,因为它依赖于fftconvolve。在某些情况下(即,对象数组或当舍入整数可能失去精度时),method='direct'总是用到的。当使用具有偶数长度输入的“相同”模式时,
correlate和correlate2d不同:它们之间有1个索引偏移。示例
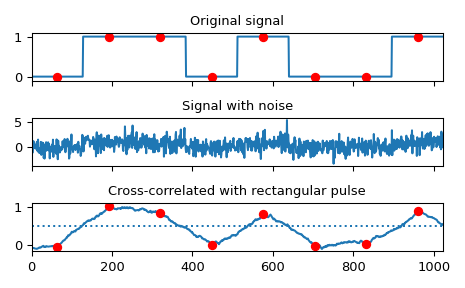
使用互相关实现匹配的过滤,以恢复通过噪声信道的信号。
>>> from scipy import signal >>> import matplotlib.pyplot as plt >>> rng = np.random.default_rng()
>>> sig = np.repeat([0., 1., 1., 0., 1., 0., 0., 1.], 128) >>> sig_noise = sig + rng.standard_normal(len(sig)) >>> corr = signal.correlate(sig_noise, np.ones(128), mode='same') / 128
>>> clock = np.arange(64, len(sig), 128) >>> fig, (ax_orig, ax_noise, ax_corr) = plt.subplots(3, 1, sharex=True) >>> ax_orig.plot(sig) >>> ax_orig.plot(clock, sig[clock], 'ro') >>> ax_orig.set_title('Original signal') >>> ax_noise.plot(sig_noise) >>> ax_noise.set_title('Signal with noise') >>> ax_corr.plot(corr) >>> ax_corr.plot(clock, corr[clock], 'ro') >>> ax_corr.axhline(0.5, ls=':') >>> ax_corr.set_title('Cross-correlated with rectangular pulse') >>> ax_orig.margins(0, 0.1) >>> fig.tight_layout() >>> plt.show()
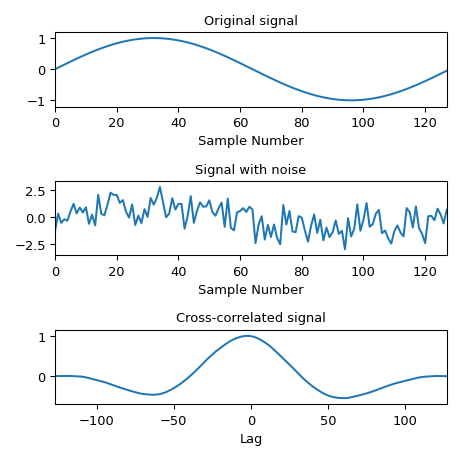
计算噪声信号与原始信号的互相关。
>>> x = np.arange(128) / 128 >>> sig = np.sin(2 * np.pi * x) >>> sig_noise = sig + rng.standard_normal(len(sig)) >>> corr = signal.correlate(sig_noise, sig) >>> lags = signal.correlation_lags(len(sig), len(sig_noise)) >>> corr /= np.max(corr)
>>> fig, (ax_orig, ax_noise, ax_corr) = plt.subplots(3, 1, figsize=(4.8, 4.8)) >>> ax_orig.plot(sig) >>> ax_orig.set_title('Original signal') >>> ax_orig.set_xlabel('Sample Number') >>> ax_noise.plot(sig_noise) >>> ax_noise.set_title('Signal with noise') >>> ax_noise.set_xlabel('Sample Number') >>> ax_corr.plot(lags, corr) >>> ax_corr.set_title('Cross-correlated signal') >>> ax_corr.set_xlabel('Lag') >>> ax_orig.margins(0, 0.1) >>> ax_noise.margins(0, 0.1) >>> ax_corr.margins(0, 0.1) >>> fig.tight_layout() >>> plt.show()