scipy.optimize.least_squares¶
- scipy.optimize.least_squares(fun, x0, jac='2-point', bounds=(- inf, inf), method='trf', ftol=1e-08, xtol=1e-08, gtol=1e-08, x_scale=1.0, loss='linear', f_scale=1.0, diff_step=None, tr_solver=None, tr_options={}, jac_sparsity=None, max_nfev=None, verbose=0, args=(), kwargs={})[源代码]¶
求解变量有界的非线性最小二乘问题。
给定残差f(X)(n个实变量的m-D实函数)和损失函数Rho(S)(标量函数),
least_squares查找成本函数F(X)的局部最小值:minimize F(x) = 0.5 * sum(rho(f_i(x)**2), i = 0, ..., m - 1) subject to lb <= x <= ub
损失函数Rho(S)的目的是减少离群值对解的影响。
- 参数
- fun可调用
计算残差向量的函数,签名为
fun(x, *args, **kwargs)即最小化相对于其第一个自变量进行。这一论点x传递给此函数的是形状为(n,)的ndarray(从不是标量,即使n=1)。它必须分配并返回形状为(m,)的一维array_like或标量。如果参数是x是复杂的还是函数fun返回复数残差,则必须将其包装在实数参数的实数函数中,如示例部分末尾所示。- x0具有形状(n,)或浮点的ARRAY_LIKE
对自变量的初步猜测。如果是Float,它将被视为只有一个元素的一维数组。
- jac{‘2点’,‘3点’,‘cs’,可调用},可选
计算雅可比矩阵(m×n矩阵,其中元素(i,j)是f的偏导数)的方法 [i] 关于x [j] )。关键字选择有限差分格式进行数值估计。方案“3点”更精确,但需要的操作是“2点”(默认)的两倍。方案“cs”使用复杂的步骤,虽然可能是最精确的,但只有在以下情况下才适用。 fun 正确地处理复杂输入,并且可以解析地继续到复杂平面。方法“lm”始终使用“2点”方案。如果可调用,则将其用作
jac(x, *args, **kwargs)并且应返回雅可比的良好近似值(或精确值),作为类似数组(应用了np.至少_2d)、稀疏矩阵(性能首选的CSR_矩阵)或scipy.sparse.linalg.LinearOperator。- boundsARRAY_LIKE的2元组,可选
自变量的上下界。默认为无边界。每个数组的大小必须与 x0 或者是标量,在后一种情况下,所有变量的界限都是相同的。使用
np.inf使用适当的符号禁用所有或部分变量的界限。- method{‘trf’,‘dogbox’,‘lm’},可选
执行最小化的算法。
‘trf’:信赖域反射算法,特别适用于有界的大型稀疏问题。一般稳健的方法。
Dogbox:带矩形信任域的Dogleg算法,典型的用例是有界的小问题。对于秩不足的雅可比问题,不推荐使用。
‘lm’:MINPACK中实现的Levenberg-MarQuardt算法。不处理边界和稀疏雅各比人。对于无约束的小问题,通常是最有效的方法。
默认值为‘TRF’。有关详细信息,请参阅注释。
- ftol浮动或无,可选
成本函数更改后的终止容差。默认值为1e-8。当出现以下情况时,优化过程将停止
dF < ftol * F在最后一步中,局部二次模型与真实模型有较好的一致性。如果无且‘method’不是‘lm’,则此条件的终止被禁用。如果‘method’为‘lm’,则此公差必须高于机器ε。
- xtol浮动或无,可选
因自变量变化而终止的容差。默认值为1e-8。确切的条件取决于 method 已使用:
对于‘TRF’和‘Dogbox’:
norm(dx) < xtol * (xtol + norm(x))。对于“lm”:
Delta < xtol * norm(xs),在哪里Delta是信任区域半径,并且xs的值是x根据比例调整 x_scale 参数(见下文)。
如果无且‘method’不是‘lm’,则此条件的终止被禁用。如果‘method’为‘lm’,则此公差必须高于机器ε。
- gtol浮动或无,可选
按梯度范数终止的公差。默认值为1e-8。确切的条件取决于 method 已使用:
对于‘TRF’:
norm(g_scaled, ord=np.inf) < gtol,在哪里g_scaled是否缩放渐变的值以考虑边界的存在 [STIR].对于“Dogbox”:
norm(g_free, ord=np.inf) < gtol,在哪里g_free是相对于边界上未处于最佳状态的变量的梯度。对于‘lm’:雅可比矩阵的列与残差向量之间的夹角余弦的最大绝对值小于 gtol ,或者残差向量为零。
如果无且‘method’不是‘lm’,则此条件的终止被禁用。如果‘method’为‘lm’,则此公差必须高于机器ε。
- x_scaleARRAY_LIKE或‘JAC’,可选
每个变量的特征尺度。设置 x_scale 等同于在缩放变量中重新表述问题。
xs = x / x_scale。另一种观点是沿第j维的信任区的大小与x_scale[j]。可以通过设置 x_scale 使得沿任何缩放变量的给定大小的步长对成本函数具有类似的影响。如果设置为‘jac’,则使用雅可比矩阵列的逆范数迭代更新刻度(如中所述 [JJMore]) 。- loss字符串或可调用,可选
确定损失函数。允许使用以下关键字值:
‘线性’(默认):
rho(z) = z。给出了一个标准的最小二乘问题。‘SOFT_L1’:
rho(z) = 2 * ((1 + z)**0.5 - 1)。L1(绝对值)损失的光滑逼近。通常是稳健最小二乘的一个很好的选择。“胡伯”:
rho(z) = z if z <= 1 else 2*z**0.5 - 1。其工作方式类似于“SOFT_L1”。“Cauchy”:
rho(z) = ln(1 + z)。严重削弱了离群点的影响,但可能会给优化过程带来困难。‘arctan’:
rho(z) = arctan(z)。限制单个残差的最大损失,具有类似于“柯西”的属性。
如果可调用,则必须使用一维ndarray
z=f**2并返回形状为(3,m)的ARRAY_LIKE,其中行0包含函数值,行1包含一阶导数,行2包含二阶导数。方法“lm”仅支持“线性”损失。- f_scale浮动,可选
内值残差和异常值残差之间的软边距值,默认值为1.0。损失函数的评估如下
rho_(f**2) = C**2 * rho(f**2 / C**2),在哪里C是 f_scale ,以及rho由以下因素决定 loss 参数。此参数对loss='linear',但对于其他 loss 它的价值是至关重要的。- max_nfevNONE或INT,可选
终止前函数求值的最大次数。如果为None(默认值),则自动选择值:
对于‘TRF’和‘Dogbox’:100*n。
对于‘lm’:100 * n if jac is callable and 100 * n*(n+1)否则(因为‘lm’在雅可比估计中计数函数调用)。
- diff_stepNONE或ARRAY_LIKE,可选
确定雅可比的有限差分近似的相对步长。实际步长计算如下
x * diff_step。如果无(默认值),则 diff_step 被认为是所使用的有限差分格式的机器ε的常规“最优”功率 [NR].- tr_solver{None,‘Exact’,‘lsmr’},可选
解决信赖域子问题的方法,仅与“TRF”和“Dogbox”方法有关。
“精确”适用于具有稠密雅可比矩阵的不是很大的问题。每次迭代的计算复杂度相当于雅可比矩阵的奇异值分解。
“lsmr”适用于具有稀疏和大型雅可比矩阵的问题。它使用迭代过程
scipy.sparse.linalg.lsmr用于寻找线性最小二乘问题的解,并且只需要矩阵向量积的计算。
如果为None(默认),则根据第一次迭代中返回的Jacobian类型选择解算器。
- tr_optionsDICT,可选
传递给信任区域求解器的关键字选项。
tr_solver='exact': tr_options 都被忽略了。tr_solver='lsmr':选项scipy.sparse.linalg.lsmr。另外,method='trf'支持‘正则化’选项(bool,默认值为True),该选项将正则化项添加到正规方程,从而在雅可比矩阵秩不足的情况下提高收敛性 [Byrd] (情商。3.4)。
- jac_sparsity{无,ARRAY_LIKE,稀疏矩阵},可选
定义了用于有限差分估计的雅可比矩阵的稀疏结构,其形状必须为(m,n)。如果雅可比函数中只有几个非零元素 each 行,提供稀疏结构将大大加快计算速度 [Curtis]. 零条目表示雅可比中的相应元素等同为零。如果提供,则强制使用“lsmr”信任区域解算器。如果为None(默认值),则将使用密集差异。对“lm”方法无效。
- verbose{0,1,2},可选
算法的详细程度:
0(默认值):静默工作。
1:显示终止报告。
2:显示迭代过程中的进度(‘lm’方法不支持)。
- Args,Kwargs,Args,Kwargs元组和字典,可选
传递给 fun 和 jac 。默认情况下两者均为空。调用签名为
fun(x, *args, **kwargs)同样的道理也适用于 jac 。
- 退货
- resultOptimizeResult
OptimizeResult定义了以下字段:- Xndarray,形状(n,)
找到解决方案。
- 成本浮动
解决方案的成本函数的值。
- 有趣的ndarray,形状(m,)
解的残差向量。
- JACndarray,稀疏矩阵或线性运算符,Shape(m,n)
修正的雅可比矩阵的解,在这个意义上,J^T J是代价函数的Hessian的高斯-牛顿近似。该类型与算法使用的类型相同。
- 评分ndarray,形状(m,)
成本函数在解处的梯度。
- 最佳性浮动
一阶最优性测度。在无约束问题中,它总是梯度的一致范数。在约束问题中,它是与之相比较的量 gtol 在迭代期间。
- active_mask整数的ndarray,Shape(n,)
每个组件都显示相应的约束是否处于活动状态(即变量是否处于边界):
0:约束未处于活动状态。
-1:下限处于活动状态。
1:上限处于活动状态。
对于“trf”方法来说可能有点随意,因为它会生成一个严格可行的迭代序列,并且 active_mask 在容差阈值内确定。
- NFEV集成
已完成的功能评估次数。与‘lm’方法相反,‘trf’和‘dogbox’方法不计算用于数值雅可比近似的函数调用。
- njev整型或无
完成的雅可比求值次数。如果在“lm”方法中使用数值雅可比近似,则将其设置为“无”。
- 状态集成
算法终止的原因:
-1:MINPACK返回的输入参数状态不正确。
0:超过函数求值的最大次数。
1: gtol 满足终止条件。
2: ftol 满足终止条件。
3: xtol 满足终止条件。
4:两者兼而有之 ftol 和 xtol 满足终止条件。
- 消息应力
终止原因的口头描述。
- 成功布尔尔
如果满足其中一个收敛条件,则为True (status >0)。
注意事项
方法‘lm’(Levenberg-MarQuardt)调用MINPACK(lmder,lmdif)中实现的最小二乘算法的包装器。它运行作为信任域类型算法的Levenberg-MarQuardt算法。它的实现是基于纸张的 [JJMore], 它非常健壮和高效,有很多聪明的技巧。它应该是您解决无约束问题的首选。请注意,它不支持边界。而且,当m<n时,它也不起作用。
方法‘TRF’(信赖域反射)是由求解方程组的过程得到的,这些方程组构成了有界约束极小化问题的一阶最优性条件,如文[1]所示 [STIR]. 该算法迭代求解增加了特殊的对角二次项的信赖域问题,信赖域的形状由距离边界的距离和梯度的方向决定。此增强功能有助于避免直接进入边界,并有效地探索整个变量空间。为了进一步提高收敛性,该算法考虑了从边界反映的搜索方向。该算法在满足理论要求的前提下,保证了迭代的严格可行性。在稠密雅可比的情况下,信赖域子问题的求解方法与文献[1]中描述的方法非常相似。 [JJMore] (并在MINPACK中实现)。与MINPACK实现的不同之处在于,雅克比矩阵的奇异值分解在每次迭代中进行一次,而不是QR分解和一系列Givens旋转消除。对于大型稀疏雅可比,采用了求解信赖域子问题的二维子空间方法 [STIR], [Byrd]. 子空间由缩放的梯度和由传递的近似高斯-牛顿解来扩展
scipy.sparse.linalg.lsmr。当不施加约束时,该算法与MINPACK非常相似,并且具有大致相当的性能。该算法对无界和有界问题都具有较强的鲁棒性,因此被选为缺省算法。方法“Dogbox”在信任域框架中操作,但考虑矩形信任域,而不是传统的椭球体 [Voglis]. 当前信赖域和初始界的交点又是矩形的,因此在每次迭代中,用Powell折线法近似求解约束约束下的二次极小化问题 [NumOpt]. 对于稠密雅可比,所需的高斯-牛顿步长可以精确计算,或者近似计算为
scipy.sparse.linalg.lsmr对于大型稀疏的雅各比人来说。当雅可比矩阵的秩小于变量个数时,算法有可能表现出较慢的收敛速度。在变量较少的有界问题上,该算法的性能往往优于“TRF”。健壮的损失函数按照中所述实施 [BA]. 其思想是在每次迭代中修改残差向量和雅可比矩阵,以使计算的梯度和高斯-牛顿海森近似与成本函数的真实梯度和海森近似相匹配。然后,算法以正常的方式进行,即鲁棒损失函数被实现为标准最小二乘算法上的简单包装器。
0.17.0 新版功能.
参考文献
- STIR(1,2,3)
M.A.Branch,T.F.Coleman,和Y.Li,“A子空间、内部和共轭梯度法求解大规模边界约束最小化问题”,SIAM Journal on Science Computing,第21卷,第1期,第1-23页,1999年。
- NR
William H.Press et.等,“数值处方,科学计算的艺术,第三版”,SEC。5.7.
- Byrd(1,2)
R·H·伯德、R·B·施纳贝尔和G·A·舒尔茨,“二维子空间上的信赖域问题的最小化近似解”,数学。“编程”,第40页,第247-263页,1988年。
- Curtis
A.Curtis,M.J.D.Powell和J.Reid,“关于稀疏雅可比矩阵的估计”,“数学研究所及其应用期刊”,第13期,第117-120页,1974年。
- JJMore(1,2,3)
J·J·莫尔,<Levenberg-MarQuardt算法:实现与理论>,“数值分析”,编辑。G.A.Watson,数学讲稿630,Springer Verlag,第105-116页,1977。
- Voglis
C.Voglis和I.E.Lagaris,“无约束和有界约束非线性优化的矩形信赖域折线方法”,WSEAS国际应用数学会议,希腊科孚,2004年。
- NumOpt
J·诺西达尔和S·J·赖特,“数值优化”,第2版,第4章。
- BA
B.Triggs et.等,“束调整-现代综合”,“视觉算法国际研讨会论文集:理论与实践”,第298-372页,1999年。
示例
在这个例子中,我们发现Rosenbrock函数的最小值在自变量上没有界限。
>>> def fun_rosenbrock(x): ... return np.array([10 * (x[1] - x[0]**2), (1 - x[0])])
请注意,我们只提供残差的向量。该算法将代价函数构造为残差的平方和,从而得到Rosenbrock函数。确切的最小值是
x = [1.0, 1.0]。>>> from scipy.optimize import least_squares >>> x0_rosenbrock = np.array([2, 2]) >>> res_1 = least_squares(fun_rosenbrock, x0_rosenbrock) >>> res_1.x array([ 1., 1.]) >>> res_1.cost 9.8669242910846867e-30 >>> res_1.optimality 8.8928864934219529e-14
我们现在约束变量,这样以前的解决方案就变得不可行了。具体地说,我们要求
x[1] >= 1.5,以及x[0]不受约束。为此,我们指定 bounds 参数设置为least_squares在表格中bounds=([-np.inf, 1.5], np.inf)。我们还提供了解析雅可比矩阵:
>>> def jac_rosenbrock(x): ... return np.array([ ... [-20 * x[0], 10], ... [-1, 0]])
把所有这些放在一起,我们可以看到新的解决方案即将出台:
>>> res_2 = least_squares(fun_rosenbrock, x0_rosenbrock, jac_rosenbrock, ... bounds=([-np.inf, 1.5], np.inf)) >>> res_2.x array([ 1.22437075, 1.5 ]) >>> res_2.cost 0.025213093946805685 >>> res_2.optimality 1.5885401433157753e-07
现在,我们求解一个包含100000个变量的Broyden三对角向量值函数的方程组(即,成本函数至少应为零):
>>> def fun_broyden(x): ... f = (3 - x) * x + 1 ... f[1:] -= x[:-1] ... f[:-1] -= 2 * x[1:] ... return f
相应的雅可比矩阵是稀疏的。我们告诉算法通过有限差分来估计它,并提供雅可比的稀疏结构来显着地加快这一过程。
>>> from scipy.sparse import lil_matrix >>> def sparsity_broyden(n): ... sparsity = lil_matrix((n, n), dtype=int) ... i = np.arange(n) ... sparsity[i, i] = 1 ... i = np.arange(1, n) ... sparsity[i, i - 1] = 1 ... i = np.arange(n - 1) ... sparsity[i, i + 1] = 1 ... return sparsity ... >>> n = 100000 >>> x0_broyden = -np.ones(n) ... >>> res_3 = least_squares(fun_broyden, x0_broyden, ... jac_sparsity=sparsity_broyden(n)) >>> res_3.cost 4.5687069299604613e-23 >>> res_3.optimality 1.1650454296851518e-11
我们还来解决一个曲线拟合问题,使用稳健的损失函数来处理数据中的异常值。将模型函数定义为
y = a + b * exp(c * t),其中t是预测变量,y是观测值,a,b,c是要估计的参数。首先,定义生成含有噪声和离群值的数据的函数,定义模型参数,生成数据:
>>> from numpy.random import default_rng >>> rng = default_rng() >>> def gen_data(t, a, b, c, noise=0., n_outliers=0, seed=None): ... rng = default_rng(seed) ... ... y = a + b * np.exp(t * c) ... ... error = noise * rng.standard_normal(t.size) ... outliers = rng.integers(0, t.size, n_outliers) ... error[outliers] *= 10 ... ... return y + error ... >>> a = 0.5 >>> b = 2.0 >>> c = -1 >>> t_min = 0 >>> t_max = 10 >>> n_points = 15 ... >>> t_train = np.linspace(t_min, t_max, n_points) >>> y_train = gen_data(t_train, a, b, c, noise=0.1, n_outliers=3)
定义用于计算残差和参数初始估计的函数。
>>> def fun(x, t, y): ... return x[0] + x[1] * np.exp(x[2] * t) - y ... >>> x0 = np.array([1.0, 1.0, 0.0])
计算标准最小二乘解:
>>> res_lsq = least_squares(fun, x0, args=(t_train, y_train))
现在用两个不同的鲁棒损失函数计算两个解。该参数 f_scale 设置为0.1,意味着Inlier残差不应显著超过0.1(使用的噪波级别)。
>>> res_soft_l1 = least_squares(fun, x0, loss='soft_l1', f_scale=0.1, ... args=(t_train, y_train)) >>> res_log = least_squares(fun, x0, loss='cauchy', f_scale=0.1, ... args=(t_train, y_train))
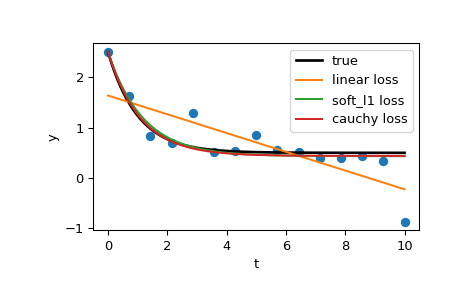
最后,绘制所有的曲线。我们通过选择适当的 loss 即使在存在强烈异常值的情况下,我们也可以得到接近最优的估计。但请记住,通常建议先尝试“SOFT_L1”或“HUBER”损失(如果有必要),因为其他两个选项可能会在优化过程中造成困难。
>>> t_test = np.linspace(t_min, t_max, n_points * 10) >>> y_true = gen_data(t_test, a, b, c) >>> y_lsq = gen_data(t_test, *res_lsq.x) >>> y_soft_l1 = gen_data(t_test, *res_soft_l1.x) >>> y_log = gen_data(t_test, *res_log.x) ... >>> import matplotlib.pyplot as plt >>> plt.plot(t_train, y_train, 'o') >>> plt.plot(t_test, y_true, 'k', linewidth=2, label='true') >>> plt.plot(t_test, y_lsq, label='linear loss') >>> plt.plot(t_test, y_soft_l1, label='soft_l1 loss') >>> plt.plot(t_test, y_log, label='cauchy loss') >>> plt.xlabel("t") >>> plt.ylabel("y") >>> plt.legend() >>> plt.show()
在下一个示例中,我们将展示如何使用优化复变量的复值残差函数
least_squares()。请考虑以下函数:>>> def f(z): ... return z - (0.5 + 0.5j)
我们将其包装成实数变量的函数,该函数只需将实数和虚数部分作为独立变量处理,即可返回实数残差:
>>> def f_wrap(x): ... fx = f(x[0] + 1j*x[1]) ... return np.array([fx.real, fx.imag])
因此,我们优化了2n个实变量的2m-D实数函数,而不是原来的n个复变量的m-D复函数:
>>> from scipy.optimize import least_squares >>> res_wrapped = least_squares(f_wrap, (0.1, 0.1), bounds=([0, 0], [1, 1])) >>> z = res_wrapped.x[0] + res_wrapped.x[1]*1j >>> z (0.49999999999925893+0.49999999999925893j)