摘要: 等比数列介绍 等比数列是说假如一个数列从第2项起，每一项与它的前一项的比值等于同一个常数。这个常数叫做等比数列的公比，公比通常用字母q表明(q≠0)，等比数列a1≠ 0。其间an中的每一项均不为0。注：q=1 时，an为常数列。 公式介绍 （1）定义式： \(...
等比数列介绍
等比数列是说假如一个数列从第2项起，每一项与它的前一项的比值等于同一个常数。这个常数叫做等比数列的公比，公比通常用字母q表明(q≠0)，等比数列a1≠ 0。其间an中的每一项均不为0。注：q=1 时，an为常数列。
公式介绍
（1）定义式：
\(a_n=a_1 * q^{n-1}\)
（2）通项公式（等比数列通项公式经过界说式叠乘而来）
（3）求和公式：
\(S_n=na_1\)（q=1）
\(S_n= \frac { a_1(1-q^n) }{1-q}\)
求和公式用文字来描绘就是：
Sn=首相（1-末项）/1-公比（公比≠1）
任意两项a_m，a_n的关系为\(a_n=a_m * q^{n-m}\)；在运用等比数列的前n项和时，必定要注意讨论公比q是不是为1.
（4）从等比数列的界说、通项公式、前n项和公式能够推出：
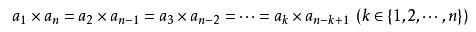
（5）等比中项：若a_qa_p=[a_r]^2，那么a_r为a_p，a_q等比中项。
记πn=a1·a2…an，则有π2n-1=(an)2n-1，π2n+1=(an+1)2n+1。
别的，一个各项均为正数的等比数列各项取同底数后构成一个等差数列；反之，以任一个正数C为底，用一个等差数列的各项做指数结构幂Can，则是等比数列。在这个含义下，咱们说：一个正项等比数列与等差数列是“同构”的。
等比中项界说：从第二项起，每一项（有穷数列的末项在外）都是它的前一项与后一项的等比中项。
等比中项公式：
\(a_{n-1}a_{n+1}=[a_n]^2\)或许\( \frac {a_n} {a_{n-1}} = \frac {a_{n+1}} {a_n} \)。
（6）无量递缩等比数列各项和公式：
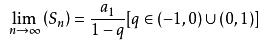
无量递缩等比数列各项和公式：公比的绝对值小于1的无量等比数列，当n无限增大时的极限叫做这个无量等比数列各项的和。
(7)由等比数列组成的新的等比数列的公比：
{an}是公比为q的等比数列
1.若A=a1+a2+……+an
B=an+1+……+a2n
C=a2n+1+……a3n
则，A、B、C构成新的等比数列，公比\(Q=q^n\)
2.若A=a1+a4+a7+……+a3n-2
B=a2+a5+a8+……+a3n-1
C=a3+a6+a9+……+a3n
则，A、B、C构成新的等比数列，公比\(Q=q\)
