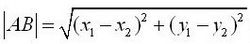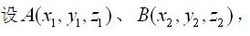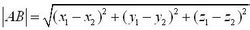摘要: 两点间距离公式 常用于函数图形内求距离、再而通过距离来求点的坐标的应用题。 平面直角坐标系中 设A(X1,Y1)、B(X2,Y2),则; 或者∣AB∣=∣X1-X2∣secα=∣Y1-Y2∣/sinα, 其中α为直线AB的倾斜角,k为直线AB的斜率。 ...
两点间距离公式
常用于函数图形内求距离、再而通过距离来求点的坐标的应用题。
平面直角坐标系中
设A(X1,Y1)、B(X2,Y2),则;
或者∣AB∣=∣X1-X2∣secα=∣Y1-Y2∣/sinα,
其中α为直线AB的倾斜角,k为直线AB的斜率。
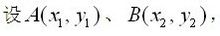
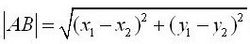
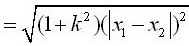
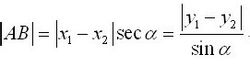
三维坐标系中
设A(x1,y1,z1),B(x2,y2,z2)
|AB|=√[(x2-x1)^2+(y2-y1)^2+(z2-z1)^2]
证明很简单,套用两次勾股定理。
两次勾股定理的套用:
第一次套用勾股定理:在三维坐标中,首先计算两点在平面坐标中的距离,也就是X,Y轴上的平面距离,这时第一次套用勾股定理计算出两点间的平面距离。
第二次套用勾股定理:已经计算出两点在X,Y轴上的平面距离,再计算出两点在Z轴上的垂直距离:Z1-Z2。这时就可以再次套用勾股定理计算出两点在三维坐标中的距离了。即:|AB|=√[(x2-x1)^2+(y2-y1)^2+(z2-z1)^2]