分数指数

1.整数指数幂的运算性质

a^m*aⁿ=a^{m+n(m,n∈ Z)}

(a^m)ⁿ=a^mn(m,n∈Z)

(ab)ⁿ=aⁿ*bⁿ(n∈Z)

2.根式的运算性质

（1）当n为任意正整数时，（n√a）ⁿ=a

（2）当n为奇数时，n√aⁿ=a

当n为偶数时，n√aⁿ=

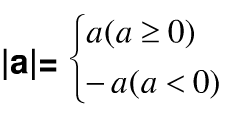
用语音叙述上面两个公式：

（1）非负实数a的n次方根的n次幂是它本身

（2）n为奇数时，实数a的n次幂的n次方根是a本身；n为偶数时，实数a的n次幂的n次方根是a的绝对值

引例：当a>0时

（1）

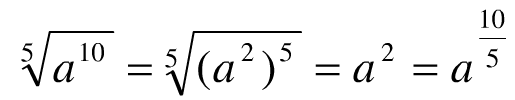
（2）

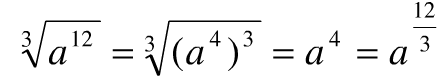
当根式的被开方数的指数能被根指数整除时，根式可以写成分数指数幂的形式。

当根式的被开方数的指数不能被根指数整除时，根式也可以写成分数指数幂的形式。