摘要: 棱锥的概念 一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。棱锥用表示顶点和底面各顶点的字母,或者用表示顶点和底面的一条对角线端点的字母来表示。如棱锥S-ABCDE,或者棱锥S-AC。 棱锥的底面: 棱锥中的多边...
棱锥的概念
一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。棱锥用表示顶点和底面各顶点的字母,或者用表示顶点和底面的一条对角线端点的字母来表示。如棱锥S-ABCDE,或者棱锥S-AC。
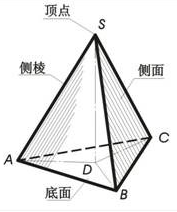
棱锥的底面: 棱锥中的多边形叫做棱锥的底面。如下图中的面ABCD就是棱锥的底面。
棱锥的侧面: 棱锥中除底面以外的各个面都叫做棱锥的侧面。如图中的面PAB、面PCD等都是棱锥的侧面。
棱锥的侧棱: 相邻侧面的公共边叫做棱锥的侧棱。如图中PA、PB等都是棱锥的侧棱。
棱锥的顶点; 棱锥中各个侧面的公共顶点叫做棱锥的顶点。如图中P是各个侧面的公共顶点,P是棱锥的顶点。
棱锥的高: 棱锥的顶点到底面的距离叫做棱锥的高。
棱锥的对角面; 棱锥中过不相邻的两条侧棱的截面叫做对角面。
棱锥的特征
棱锥是多面体中重要的一种,它有两个本质特征:①有一个面是多边形;②其余的各面是有一个公共顶点的三角形,二者缺一不可。因此棱锥有一个面是多边形,其余各面都是三角形。但是也要注意“有一个面是多边形,其余各面都是三角形”的几何体未必是棱锥。
棱锥的相关公式
\(S侧=S1+S2+…+Sn\)(其中Si,i=1,2…n为第i个侧面的面积)
\(S全=S侧+S底\)
\(V=1/3S底h\)(S为锥体的底面积,h为锥体的高).
斜棱锥的侧面积=各侧的面积之和
正棱锥的侧面积:\(S正棱锥侧=1/2chˊ\)(c为底面周长,hˊ为斜高)
棱锥的中截面面积:\(S中截面=1/4S底\)
