4.7.2.2. 均方位移 MDAnalysis.analysis.msd

作者:

雨果·麦克德莫特--Opeskin

年:

2020

版权所有:

GNU公共许可证v2

该模块实现了由爱因斯坦关系计算均方位移(MSD)。MSD可以用来描述粒子运动的速度，它起源于对布朗运动的研究。关于MSD背后的理论和随后的自扩散系数的计算的完整解释，请将读者引导至 [Maginn2018] 。MSD可以通过以下表达式计算，称为 Einstein formula ：

\[Msd(r_{d})=\Bigg{\Lange}\FRAC{1}{N}\sum_{i=1}^{N}|r_{d} -r_{d}(T_0)|^2\Bigg{\Rangle}_{t_{0}}\]

哪里 \(N\) 是计算MSD的等效粒子数， \(r\) 是它们的坐标和 \(d\) MSD的所需维度。请注意，虽然MSD的定义是通用的，但计算MSD有许多实际注意事项，不同的实现会有所不同。在本模块中，我们将计算加窗的MSD，其中MSD是所有可能的滞后时间的平均值 \(\tau \le \tau_{{max}}\) ，在哪里 \(\tau_{{max}}\) 是轨迹的长度，从而最大化样本数。

以这种方式计算MSD可能是计算密集型的，因为它的 \(N^2\) 相对于以下方面进行缩放 \(\tau_{{max}}\) 。一种计算MSD的算法 \(N log(N)\) 基于快速傅里叶变换的缩放是已知的，并且可以通过设置 fft=True [Calandri2011] [Buyl2018] 。基于FFT的方法要求 tidynamics 包已安装；否则代码将引发 ImportError 。

请举出 [Calandri2011] [Buyl2018] 如果您在正常的MDAnalysis引用之外使用此模块。

警告

要使用此分析模块正确计算MSD，必须在 展开 这是惯例。也就是说，当原子通过周期边界时，它们不能 包好 回到主模拟单元格。MDAnalysis目前不在 MDAnalysis.transformations API，尽管具有相似名称的函数。我们计划在未来实施适当的转型。与此同时，各种模拟包提供了将坐标转换为展开约定的实用程序。例如，在GROMACS中，这可以使用 gmx trjconv 使用 -pbc nojump 旗帜。

4.7.2.2.1. 计算MSD

此示例计算100个粒子进行随机行走的移动的3D MSD。使用作为MDAnalysis测试套件一部分提供的文件(在变量中 RANDOM_WALK 和 RANDOM_WALK_TOPO )

首先加载所有模块和测试数据

import MDAnalysis as mda
import MDAnalysis.analysis.msd as msd
from MDAnalysis.tests.datafiles import RANDOM_WALK_TOPO, RANDOM_WALK

给定一个包含轨迹数据的宇宙，可以使用类来提取MSD分析 EinsteinMSD

u = mda.Universe(RANDOM_WALK_TOPO, RANDOM_WALK)
MSD = msd.EinsteinMSD(u, select='all', msd_type='xyz', fft=True)
MSD.run()

然后，可以通过以下方式访问MSD

msd =  MSD.results.timeseries
MSD的目视检查很重要，所以让我们用一个

简单的情节。

import matplotlib.pyplot as plt
nframes = MSD.n_frames
timestep = 1 # this needs to be the actual time between frames
lagtimes = np.arange(nframes)*timestep # make the lag-time axis
fig = plt.figure()
ax = plt.axes()
# plot the actual MSD
ax.plot(lagtimes, msd, lc="black", ls="-", label=r'3D random walk')
exact = lagtimes*6
# plot the exact result
ax.plot(lagtimes, exact, lc="black", ls="--", label=r'$y=2 D\tau$')
plt.show()

这给了我们关于滞后时间的MSD的曲线图 (\(\tau\) )。我们可以看到，MSD对于以下各项近似成线性 \(\tau\) 。这是一个已知理论结果的数值例子，即随机游动的MSD关于滞后时间是线性的，斜率为 \(2d\) 。在这个表达式中 \(d\) 是MSD的维度。对于我们的3D MSD，这是3。为了进行比较，我们绘制了这条线 \(y=6\tau\) 3D随机游动的集合应该汇聚到该集合。

MSD图

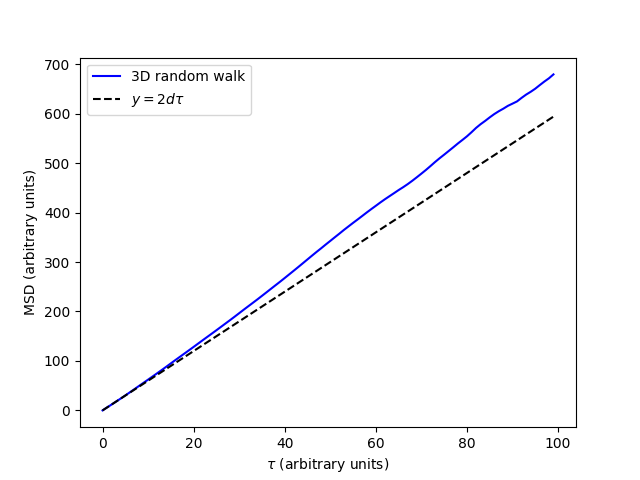
请注意，MSD的一段需要是线性的，才能准确地确定自扩散系数。这个线性段代表所谓的MSD图的“中间”，在那里，短时间滞后的弹道轨迹与长时间滞后的平均较差的数据一起被排除在外。我们可以通过索引MSD和时滞来选择MSD的“中间”。MSD的适当线性段可以用通常推荐的对数-对数曲线图来确认 [Maginn2018] 其中“中间”段可以被标识为具有1的斜率。

plt.loglog(lagtimes, msd)
plt.show()

既然我们已经确定了要分析的MSD的哪一部分，让我们来计算自扩散系数。

4.7.2.2.2. 计算自扩散系数

自扩散系数与MSD密切相关。

\[D_d=\FRAC{1}{2d}\LIM_{t\to\inty}\FRAC{d}{dt}MSD(r_{d})\]

来自MSD的自扩散系数 \(D\) 具有所需的维度 \(d\) 可以通过将相对于滞后时间的MSD拟合到线性模型来计算。下面显示了一个这样的示例，它使用在上面的示例中计算的MSD。中间的线段 \(\tau = 20\) 和 \(\tau = 60\) 用于演示MSD段的选择。

from scipy.stats import linregress
start_time = 20
start_index = int(start_time/timestep)
end_time = 60
linear_model = linregress(lagtimes[start_index:end_index],
                                              msd[start_index:end_index])
slope = linear_model.slope
error = linear_model.stderr
# dim_fac is 3 as we computed a 3D msd with 'xyz'
D = slope * 1/(2*MSD.dim_fac)

我们现在已经计算出了一个自扩散系数！

4.7.2.2.3. 组合多个副本

在计算MSD时，通常会合并重复项。下面使用MSD1和MSD2显示了一个这样的示例。

u1 = mda.Universe(RANDOM_WALK_TOPO, RANDOM_WALK)
MSD1 = msd.EinsteinMSD(u1, select='all', msd_type='xyz', fft=True)
MSD1.run()

u2 = mda.Universe(RANDOM_WALK_TOPO, RANDOM_WALK)
MSD2 = msd.EinsteinMSD(u2, select='all', msd_type='xyz', fft=True)
MSD2.run()

combined_msds = np.concatenate((MSD1.results.msds_by_particle,
                                MSD2.results.msds_by_particle), axis=1)
average_msd = np.mean(combined_msds, axis=1)

由于在第一个轨迹的最后一帧和下一个轨迹的帧0之间的跳跃将导致MSD的人为膨胀以及由此计算的任何后续扩散系数，因此不能通过在单个运行中连接复制品来实现同样的目的。

备注

在建立和处理用于计算自扩散系数的轨迹时，必须考虑几个因素。其中包括有关模拟设置的特定说明、使用展开轨迹以及在保存的帧之间保持相对较小的运行时间。此外，对有限尺寸效应的校正有时与估计误差的各种手段一起使用 [Yeh2004, von Bülow2020] 读者可参考下面的评论，其中描述了许多常见的陷阱 [Maginn2018] 。还有其他方法可以计算自扩散率，例如通过格林-久保积分。目前，这些方法不在本模块的讨论范围内。

还要注意的是，MSD的计算非常耗费内存。如果这被证明是一个问题，那么明智地使用 start ， stop ， step 可能需要控制合并哪些帧的关键字。

引用

[Maginn2018] (1,2,3,4,5,6,7,8,9)

Edward J. Maginn, Richard A. Messerly, Daniel J. Carlson, Daniel R. Roe, and J. Richard Elliot. Best practices for computing transport properties self-diffusivity and viscosity from equilibrium molecular dynamics. Living Journal of Computational Molecular Science, 1(1):6324, Dec. 2018. URL: https://livecomsjournal.org/index.php/livecoms/article/view/v1i1e6324, doi:10.33011/livecoms.1.1.6324.

[Yeh2004] (1,2,3)

In-Chul Yeh and Gerhard Hummer. System-size dependence of diffusion coefficients and viscosities from molecular dynamics simulations with periodic boundary conditions. The Journal of Physical Chemistry B, 108(40):15873–15879, 2004. doi:10.1021/jp0477147.

[von Bülow2020] (1,2,3)

Sören von Bülow, Jakob Tómas Bullerjahn, and Gerhard Hummer. Systematic errors in diffusion coefficients from long-time molecular dynamics simulations at constant pressure. The Journal of Chemical Physics, 153(2):021101, 2020. doi:10.1063/5.0008316.