scipy.integrate.solve_bvp¶
- scipy.integrate.solve_bvp(fun, bc, x, y, p=None, S=None, fun_jac=None, bc_jac=None, tol=0.001, max_nodes=1000, verbose=0, bc_tol=None)[源代码]¶
解一个常微分方程组的边值问题。
此函数以数值方式求解受两点边界条件约束的一阶常微分方程系统:
dy / dx = f(x, y, p) + S * y / (x - a), a <= x <= b bc(y(a), y(b), p) = 0
这里x是一维自变量,y(X)是N维矢量值函数,p是未知参数的k-D矢量,它将与y(X)一起找到。对于要确定的问题,必须有n+k个边界条件,即BC必须是(n+k)-D函数。
系统右侧的最后一个单数项是可选的。它由n乘以n的矩阵S定义,使得解必须满足Sy(A)=0。此条件将在迭代过程中强制执行,因此它不能与边界条件冲突。看见 [2] 用于解释在数值求解边值问题时如何处理这一项。
复杂领域中的问题也可以解决。在这种情况下,y和p被认为是复数,f和bc被假定为复值函数,但x保持为实数。请注意,f和bc必须是复数可微的(满足Cauchy-Riemann方程 [4]) ,否则你应该分别重写实部和虚部的问题。要解决复杂领域中的问题,请使用复杂数据类型传递y的初始猜测(见下文)。
- 参数
- fun可调用
系统的右侧。调用签名为
fun(x, y),或fun(x, y, p)如果参数存在。所有参数都是ndarray:x形状为(m,),y形状为(n,m),意思是y[:, i]对应于x[i],以及p形状为(k,)。返回值必须是形状为(n,m)且布局与相同的数组y。- bc可调用
计算边界条件残差的函数。调用签名为
bc(ya, yb),或bc(ya, yb, p)如果参数存在。所有参数都是ndarray:ya和yb形状(n,),和p形状为(k,)。返回值必须是形状为(n+k,)的数组。- x类似阵列,形状(m,)
初始网格。必须是一个严格递增的实数序列
x[0]=a和x[-1]=b。- y类似数组,形状(n,m)
对网格节点处函数值的初始猜测,第i列对应于
x[i]。对于复杂域过程中的问题 y 具有复杂数据类型(即使最初的猜测是纯真实的)。- p具有形状(k,)的ARRAY_LIKE或NONE,可选
对未知参数的初步猜测。如果为None(默认值),则假定问题与任何参数无关。
- S具有Shape(n,n)或None的ARRAY_LIKE
定义单数项的矩阵。如果为None(默认值),则不使用单数项即可解决问题。
- fun_jac可调用或无,可选
函数计算f关于y和p的导数。调用签名是
fun_jac(x, y),或fun_jac(x, y, p)如果参数存在。返回必须按以下顺序包含1或2个元素:df_dy:形状为(n,n,m)的类似数组,其中元素(i,j,q)等于df_i(x_q,y_q,p)/d(Y_Q)_j。
df_dp:形状为(n,k,m)的类似数组,其中元素(i,j,q)等于df_i(x_q,y_q,p)/dp_j。
这里,q表示定义了x和y的节点,而i和j表示矢量分量。如果在没有未知参数的情况下解决问题,则不应返回df_dp。
如果 fun_jac 为NONE(默认值),则导数将由正向有限差分估计。
- bc_jac可调用或无,可选
函数计算BC关于ya、yb和p的导数。调用签名为
bc_jac(ya, yb),或bc_jac(ya, yb, p)如果参数存在。返回必须包含2或3个元素,顺序如下:dbc_dya:形状为(n,n)的类似数组,其中元素(i,j)等于dbc_i(ya,yb,p)/dya_j。
dbc_dyb:形状为(n,n)的类似数组,其中元素(i,j)等于dbc_i(ya,yb,p)/dyb_j。
dbc_dp:形状为(n,k)的类似数组,其中元素(i,j)等于dbc_i(ya,yb,p)/dp_j。
如果在没有未知参数的情况下解决问题,则不应返回DBC_DP。
如果 bc_jac 为NONE(默认值),则导数将由正向有限差分估计。
- tol浮动,可选
解决方案的所需公差。如果我们定义
r = y' - f(x, y),其中y是找到的解,则求解器尝试在每个网格间隔上实现norm(r / (1 + abs(f)) < tol,在哪里norm以均方根意义估计(使用数值求积公式)。默认值为1e-3。- max_nodes整型,可选
允许的最大网格节点数。如果超过,算法将终止。默认值为1000。
- verbose{0,1,2},可选
算法的详细程度:
0(默认值):静默工作。
1:显示终止报告。
2:显示迭代过程中的进度。
- bc_tol浮动,可选
边界条件残差的所需绝对公差: bc 值应满足
abs(bc) < bc_tol组件方式。等于 tol 默认情况下。最多允许10次迭代才能达到此容差。
- 退货
- 捆绑定义了以下字段的对象:
- solPPoly
找到Y AS的解决方案
scipy.interpolate.PPoly实例,C1连续三次样条曲线。- pndarray或None,Shape(k,)
找到参数。如果问题中不存在参数,则返回None。
- xndarray,形状(m,)
最终网格的节点。
- yndarray,形状(n,m)
网格节点处的解算值。
- ypndarray,形状(n,m)
网格节点处的解导数。
- rms_residualsndarray,形状(m-1,)
每个网格间隔内的相对残差值的均方根值(请参阅的说明 tol 参数)。
- niter集成
已完成的迭代数。
- status集成
算法终止原因:
0:算法收敛到所需的精度。
1:已超过最大网格节点数。
2:求解配置系统时遇到的奇异雅可比。
- message字符串
终止原因的口头描述。
- success布尔尔
如果算法收敛到所需的精度,则为true (
status=0)。
注意事项
此函数实现四阶配置算法,其残差控制类似于 [1]. 配置系统由带有仿射不变准则函数的阻尼牛顿法求解,如中所述 [3].
请注意,在 [1] 积分残差是在没有按区间长度进行归一化的情况下定义的。因此,它们的定义与这里使用的定义不同,乘数为h**0.5(h是区间长度)。
0.18.0 新版功能.
参考文献
- 1(1,2)
J.Kierzenka,L.F.Shampine,“一个基于残差控制和Maltab PSE的BVP求解器”,ACM Trans。数学课。软文,第27卷,第3号,第299-316页,2001年。
- 2
作者:L.F.Shampine,P.H.Muir,H.Xu,“一个界面友好的Fortran BVP求解器”。
- 3
U.Ascher,R.Mattheij和R.Russell,“常微分方程边值问题的数值解”。
- 4
Cauchy-Riemann equations 在维基百科上。
示例
在第一个示例中,我们解决了Bratu的问题:
y'' + k * exp(y) = 0 y(0) = y(1) = 0
对于k=1。
我们将方程重写为一阶系统,并实现其右侧求值:
y1' = y2 y2' = -exp(y1)
>>> def fun(x, y): ... return np.vstack((y[1], -np.exp(y[0])))
实施边界条件残差的评估:
>>> def bc(ya, yb): ... return np.array([ya[0], yb[0]])
定义具有5个节点的初始网格:
>>> x = np.linspace(0, 1, 5)
众所周知,这个问题有两种解决方案。为了同时获得它们,我们对y使用两种不同的初始猜测。我们用下标a和b表示它们。
>>> y_a = np.zeros((2, x.size)) >>> y_b = np.zeros((2, x.size)) >>> y_b[0] = 3
现在我们准备好运行求解器了。
>>> from scipy.integrate import solve_bvp >>> res_a = solve_bvp(fun, bc, x, y_a) >>> res_b = solve_bvp(fun, bc, x, y_b)
让我们画出这两个找到的解决方案。我们利用样条形式的解来生成平滑的图形。
>>> x_plot = np.linspace(0, 1, 100) >>> y_plot_a = res_a.sol(x_plot)[0] >>> y_plot_b = res_b.sol(x_plot)[0] >>> import matplotlib.pyplot as plt >>> plt.plot(x_plot, y_plot_a, label='y_a') >>> plt.plot(x_plot, y_plot_b, label='y_b') >>> plt.legend() >>> plt.xlabel("x") >>> plt.ylabel("y") >>> plt.show()
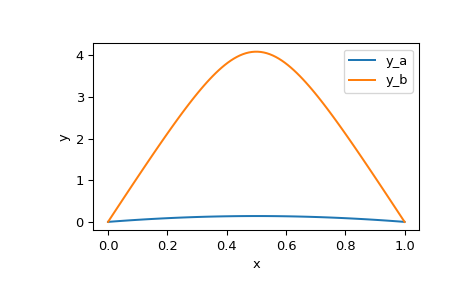
我们看到这两个解决方案具有相似的形状,但在规模上有很大的不同。
在第二个示例中,我们解决了一个简单的Sturm-Liouville问题:
y'' + k**2 * y = 0 y(0) = y(1) = 0
已知非平凡解y=A SIN(k x)对于k=π*n是可能的,其中n是整数。为了建立归一化常数A=1,我们添加一个边界条件:
y'(0) = k
同样,我们将方程重写为一阶系统,并实现其右侧求值:
y1' = y2 y2' = -k**2 * y1
>>> def fun(x, y, p): ... k = p[0] ... return np.vstack((y[1], -k**2 * y[0]))
请注意,参数p作为向量传递(在我们的示例中只有一个元素)。
实施边界条件:
>>> def bc(ya, yb, p): ... k = p[0] ... return np.array([ya[0], yb[0], ya[1] - k])
设置初始网格并猜测y。我们的目标是找到k=2的解 Pi,为了实现这一点,我们将y的值设置为大致跟随sin(2 Pi*x):
>>> x = np.linspace(0, 1, 5) >>> y = np.zeros((2, x.size)) >>> y[0, 1] = 1 >>> y[0, 3] = -1
使用6作为k的初始猜测来运行求解器。
>>> sol = solve_bvp(fun, bc, x, y, p=[6])
我们看到找到的k大致正确:
>>> sol.p[0] 6.28329460046
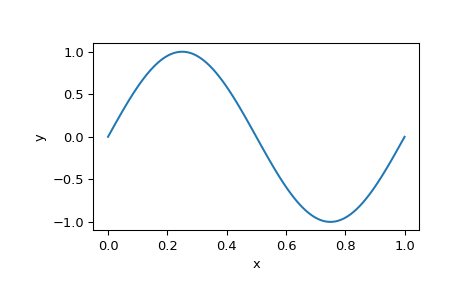
最后,绘制解决方案以查看预期的正弦曲线:
>>> x_plot = np.linspace(0, 1, 100) >>> y_plot = sol.sol(x_plot)[0] >>> plt.plot(x_plot, y_plot) >>> plt.xlabel("x") >>> plt.ylabel("y") >>> plt.show()