摘要: 圆是不论何时何地都能看到的图形,例如:大本钟,太阳,月亮等等。到底圆这个美丽的图形是被定义的呢? 圆是一种几何图形,指的是平面中到一个定点距离为定值的所有点的集合。这个给定的点称为圆的圆心。 圆形,是一个看起来比较简单的图形,实际上它是非常奇妙的形状。古人最早...
圆是不论何时何地都能看到的图形,例如:大本钟,太阳,月亮等等。到底圆这个美丽的图形是被定义的呢?
圆是一种几何图形,指的是平面中到一个定点距离为定值的所有点的集合。这个给定的点称为圆的圆心。
圆形,是一个看起来比较简单的图形,实际上它是非常奇妙的形状。古人最早是从太阳、农历十五的月亮得到圆的概念的。在很久以前的山顶洞人曾经在兽牙、砾石和石珠上钻孔,那些孔有的就很圆。到了陶器年代,很多陶器都是圆的。圆的陶器是将泥土放在一个转盘上制成的。当大家开始织线,又做了圆形的石纺锤或陶纺锤。古人还发现搬运圆的木头时滚着走对比省劲。后来他们在转移重物的时候,就把几段圆木垫在大树、大石头下面滚着走,这样当然比扛着走省劲得多。
大约在6000年前,美索不达米亚人,做出了世界上第一个轮子——圆型的木盘。大约在4000多年前,人类将圆的木盘固定在木架下,这就成了最初的车子。
就算会作圆,但不必定就懂得圆的性质。古代埃及人就以为:圆,是神赐给人的神圣图形。一直到两千多年前我国的墨子才给圆下了一个定义:圆,一中同长也。
意思是说:圆有一个圆心,圆心到圆周的长都持平。这个定义比希腊数学家欧几里得给圆下定义要早100年。
那么圆都有哪些性质呢?
(1)圆是轴对称图形,其对称轴是任意一条经过圆心的直线。圆也是中心对称图形,其对称中心是圆心。垂径定理:垂直于弦的直径平分这条弦,而且平分弦所对的2条弧。逆定理:平分弦(不是直径)的直径垂直于弦,而且平分弦所对的2条弧。
(2)关于圆周角和圆心角的性质和定理
①在同圆或等圆中,假如两个圆心角,两个圆周角,两组弧,两条弦,两条弦心距中有一组量相等,那么他们所对应的其他各组量都相同。
②在同圆或等圆中,相等的弧所对的圆周角等于它所对的圆心角的一半。
直径所对的圆周角是直角。90度的圆周角所对的弦是直径。
圆心角计算公式: θ=(L/2πr)×360°=180°L/πr=L/r(弧度)。
即圆心角的度数等于它所对的弧的度数;圆周角的度数等于它所对的弧的度数的一半。
③假如一条弧的长是另一条弧的2倍,那其所对的圆周角和圆心角是另一条弧的2倍。
(3)有关外接圆和内切圆的性质和定理(如图:)
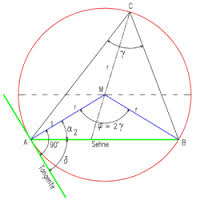
①一个三角形有唯一断定的外接圆和内切圆。外接圆圆心是三角形各边垂直平分线的交点,到三角形三个顶点间隔持平;
②内切圆的圆心是三角形各内角平分线的交点,到三角形三边间隔相同。
③R=2S△÷L(R:内切圆半径,S:三角形面积,L:三角形周长)。
④两相切圆的连心线过切点。
⑤圆O中的弦PQ的中点M,过点M任作两弦AB,CD,弦AD与BC各自交PQ于X,Y,则M为XY之中点。
(4)假如两圆相交,那么连接两圆圆心的线段垂直平分公共弦。
(5)弦切角的度数等于它所夹的弧的度数的一半。
(6)圆内角的度数等于这个角所对的弧的度数之和的一半。
(7)圆外角的度数等于这个角所截两段弧的度数之差的一半。
(8)周长相等,圆面积比正方形、长方形、三角形的面积大。
关于圆的计算公式,
1、圆的周长为C=2πr(r为半径)或者C=πd(d为直径);
2、圆的面积为S=πr2;
3、圆的直径d=2r;
4、圆中的扇形弧长L=n°πr/180°(n为圆心角);
5、圆中的扇形面积S=nπ r²/360=Lr/2(L为扇形的弧长);
6、圆锥侧面积 S=πrl(l为母线长);
7、圆锥底面半径 r=n°/360°L(L为母线长)(r为底面半径)。
圆的应用也是非常的广泛的。比如说现在的汽车车胎就是圆形的,方向盘也是圆形的,电风扇等等,所以说我们已经离不开这个奇妙的图形-圆形。
