复数减法的运算

复数的减法运算

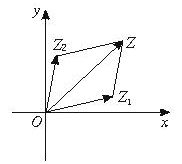
复数减法的几何意义：如图所示，复数的减法运算是加法运算的逆运算．设0Z1及0Z2分别与复数 \(a＋bi\) 及复数 \(c＋di\) 对应，且不共线，则OZ所表示的向量Z2Z1就是与复数 \((a－c)＋(b－d)i\) 对应的向量

复数减法由计算器编程来执行减法运算的两个复数运算在线工具。复数 \(a + bi\) 形式，其中a和b都是实数的表达。如果 \(z = a + bi\) 的是一个复数，然后被称为a和b的实部和虚部的z，分别表示为（z）的和Im（z）的。使用复杂的数字在许多科学领域，包括工程，电磁学，量子物理学，应用数学理论。因此， 有必要学习复杂的数字运算。

从公式中可以推导出两个复数z1和z2之间的减法

\(z1 = a + bj\)

\(z2 = c + dj\)

复数减法公式：

\(z1 + z2 = (a + bj) - (c + dj) = (a - c) + (b - d)j\)