摘要: 素数定理 下面是对π(x)更好的估计: x→ ∞,\(Li(x)=∫^x_2 \frac {dt}{logt}\).而关系式右边第二项是误差估计,详见大O符号。下表比较了π(x),x/ln x和Li(x): x π(x) π(x) - x/ln(x) Li(...
素数定理
下面是对π(x)更好的估计:
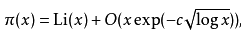
x→ ∞,\(Li(x)=∫^x_2 \frac {dt}{logt}\).而关系式右边第二项是误差估计,详见大O符号。下表比较了π(x),x/ln x和Li(x): x π(x) π(x) - x/ln(x) Li(x) - π(x) x/π(x)
(如图所示)
素数定理
| x | π(x) | π(x)-x/ln(x) | li(x)-π(x) | x/π(x) |
|---|---|---|---|---|
| 101 | 4 | 0 | 2 | 2.500 |
| 102 | 25 | 3 | 5 | 4.000 |
| 103 | 168 | 23 | 10 | 5.952 |
| 104 | 1.229 | 143 | 17 | 8.137 |
| 105 | 9,592 | 906 | 38 | 10.430 |
| 106 | 78,498 | 6,116 | 130 | 12.740 |
| 107 | 664,579 | 44,159 | 339 | 15.050 |
| 108 | 5,761,455 | 332,774 | 754 | 17.360 |
| 109 | 50,847,534 | 2,592,592 | 1,701 | 19.670 |
| 1010 | 455,052,511 | 20,758,029 | 3,104 | 21.980 |
| 1011 | 4,118,054,813 | 169,923,159 | 11,588 | 24.280 |
| 1012 | 37,607,912,018 | 1,416,705,193 | 38,263 | 26.590 |
| 1013 | 346,065,536,839 | 11,992,858,452 | 108,971 | 28.900 |
| 1014 | 3,204,941,750,802 | 102,838,308,636 | 314,890 | 31.200 |
| 1015 | 29,844,570,422,669 | 891,604,962,452 | 1,052,619 | 35.810 |
| 1016 | 279,238,341,033,925 | 7,804,289,844,392 | 3,214,632 | 35.810 |
| 4 * 1016 | 1,075,292,778,753,150 | 28,929,900,579,949 | 5,538,861 | 37.200 |
素数定理可以给出第n个素数p(n)的渐近估计:p(n)~nlogn.它也给出从整数中抽到素数的概率。从不大于自然数随机选择一个,它是素数的概率大约是1/ln n.
