10.6. OpenCV中的K-均值聚类¶

10.6.1. 目标¶

学会使用 cv2.kmeans（） OpenCV中的数据聚类功能

10.6.2. 了解参数¶

输入参数¶

样品：应该是 np.float32 数据类型，每个特性都应该放在一个列中。

N类（K） ：结束时所需的群集数

标准：这是迭代终止条件。当满足此条件时，算法迭代停止。实际上，它应该是由3个参数组成的元组。他们是 ( type, max_iter, epsilon ) ：

3.a-终止条件的类型：它有3个标志，如下所示：

cv2.TERM_CRITERIA_EPS -如果指定精度，则停止算法迭代， ε ，已到达。 cv2.TERM_CRITERIA_MAX_ITER -在指定的迭代次数后停止算法， max_iter . cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER -满足上述任一条件时停止迭代。

3.b-max_iter-指定最大迭代次数的整数。

3.c-epsilon-所需精度

尝试：标志，指定使用不同初始标记执行算法的次数。算法返回产生最佳紧性的标签。这种紧凑性作为输出返回。

旗帜：此标志用于指定初始中心的获取方式。通常使用两个标志： cv2.KMEANS_PP_CENTERS 和 cv2.KMEANS_RANDOM_CENTERS .

输出参数¶

致密性 ：这是从每个点到其对应中心的平方距离之和。

标签：这是标签数组（与上一篇文章中的“code”相同），其中每个元素都标记为“0”、“1”…。。

中心：这是群集中心的数组。

现在我们将通过三个例子来看看如何应用K-均值算法。

10.6.3. 一。只有一个特征的数据¶

考虑一下，你有一组只有一个特征的数据，即一维。例如，我们可以解决我们的t恤问题，你只需要用人的身高来决定t恤的尺寸。

所以我们首先创建数据并将其绘制在Matplotlib中

>>> %matplotlib inline
>>>
>>> import numpy as np
>>> import cv2 as cv
>>> from matplotlib import pyplot as plt
>>> x = np.random.randint(25,100,25)
>>> y = np.random.randint(175,255,25)
>>> z = np.hstack((x,y))
>>> z = z.reshape((50,1))
>>> z = np.float32(z)
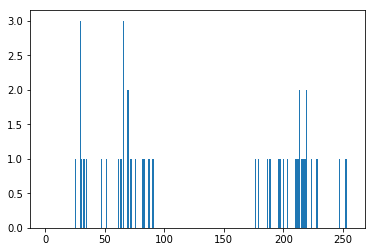
>>> plt.hist(z,256,[0,256]),plt.show()

((array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
         0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 3., 1., 0., 1., 0.,
         1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0.,
         1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 1., 0., 3., 0., 0.,
         0., 2., 0., 1., 1., 0., 0., 1., 0., 0., 0., 0., 0., 1., 1., 1., 0.,
         0., 1., 1., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
         0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
         0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
         0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
         0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
         0., 0., 0., 0., 0., 0., 1., 0., 0., 1., 0., 0., 0., 0., 0., 0., 1.,
         0., 1., 1., 0., 0., 0., 0., 0., 0., 1., 1., 0., 0., 1., 0., 0., 1.,
         0., 0., 0., 0., 0., 0., 1., 1., 1., 2., 0., 1., 1., 1., 1., 2., 0.,
         0., 0., 1., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
         0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 1., 1., 0.,
         0.]),
  array([  0.,   1.,   2.,   3.,   4.,   5.,   6.,   7.,   8.,   9.,  10.,
          11.,  12.,  13.,  14.,  15.,  16.,  17.,  18.,  19.,  20.,  21.,
          22.,  23.,  24.,  25.,  26.,  27.,  28.,  29.,  30.,  31.,  32.,
          33.,  34.,  35.,  36.,  37.,  38.,  39.,  40.,  41.,  42.,  43.,
          44.,  45.,  46.,  47.,  48.,  49.,  50.,  51.,  52.,  53.,  54.,
          55.,  56.,  57.,  58.,  59.,  60.,  61.,  62.,  63.,  64.,  65.,
          66.,  67.,  68.,  69.,  70.,  71.,  72.,  73.,  74.,  75.,  76.,
          77.,  78.,  79.,  80.,  81.,  82.,  83.,  84.,  85.,  86.,  87.,
          88.,  89.,  90.,  91.,  92.,  93.,  94.,  95.,  96.,  97.,  98.,
          99., 100., 101., 102., 103., 104., 105., 106., 107., 108., 109.,
         110., 111., 112., 113., 114., 115., 116., 117., 118., 119., 120.,
         121., 122., 123., 124., 125., 126., 127., 128., 129., 130., 131.,
         132., 133., 134., 135., 136., 137., 138., 139., 140., 141., 142.,
         143., 144., 145., 146., 147., 148., 149., 150., 151., 152., 153.,
         154., 155., 156., 157., 158., 159., 160., 161., 162., 163., 164.,
         165., 166., 167., 168., 169., 170., 171., 172., 173., 174., 175.,
         176., 177., 178., 179., 180., 181., 182., 183., 184., 185., 186.,
         187., 188., 189., 190., 191., 192., 193., 194., 195., 196., 197.,
         198., 199., 200., 201., 202., 203., 204., 205., 206., 207., 208.,
         209., 210., 211., 212., 213., 214., 215., 216., 217., 218., 219.,
         220., 221., 222., 223., 224., 225., 226., 227., 228., 229., 230.,
         231., 232., 233., 234., 235., 236., 237., 238., 239., 240., 241.,
         242., 243., 244., 245., 246., 247., 248., 249., 250., 251., 252.,
         253., 254., 255., 256.], dtype=float32),
  <a list of 256 Patch objects>),
 None)

所以我们有一个大小为50的数组'z'，值从0到255。我把“z”改成了列向量。当存在多个功能时，它将更加有用。然后我制作了np.float32类型的数据。

我们得到以下图像：

现在我们应用KMeans函数。在此之前，我们需要指定 \(criteria\) . 我的标准是，只要运行10次算法迭代，或者 epsilon = 1.0 到达时，停止算法并返回答案。

>>> # Define criteria = ( type, max_iter = 10 , epsilon = 1.0 )
>>> criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 10, 1.0)
>>> # Set flags (Just to avoid line break in the code)
>>> flags = cv.KMEANS_RANDOM_CENTERS
>>> # Apply KMeans
>>> compactness,labels,centers = cv.kmeans(z,2,None,criteria,10,flags)

这给了我们紧凑性，标签和中心。在这种情况下，我得到的中心是60和207。标签的大小与测试数据的大小相同，其中每个数据将根据其质心标记为“0”、“1”、“2”等。现在，我们根据标签将数据分成不同的集群。

>>> A = z[labels==0]
>>> B = z[labels==1]

现在我们用红色绘制A，用蓝色绘制B，用黄色绘制质心。

>>> # Now plot 'A' in red, 'B' in blue, 'centers' in yellow
>>> plt.hist(A,256,[0,256],color = 'r')
>>> plt.hist(B,256,[0,256],color = 'b')
>>> plt.hist(centers,32,[0,256],color = 'y')
>>> plt.show()

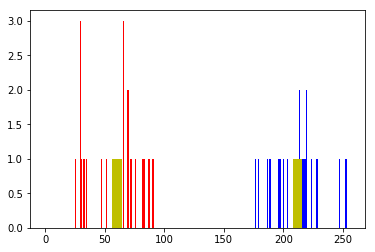
下面是我们得到的输出：

10.6.4. 2。多功能数据¶

在上一个例子中，我们只考虑了t恤问题的高度。在这里，我们要兼顾身高和体重。

记住，在前面的例子中，我们将数据转换为一个列向量。每个特性都排列在一列中，而每一行对应于一个输入测试样本。

例如，在本例中，我们设置了一个50x2大小的测试数据，即50人的身高和体重。第一列对应所有50人的身高，第二列对应他们的体重。第一行包含两个元素，第一个元素是第一个人的身高，第二个元素是他的体重。同样，剩余的行对应于其他人的身高和体重。检查下面的图像：

现在我直接转到代码：

>>> import numpy as np
>>> import cv2 as cv
>>> from matplotlib import pyplot as plt
>>> X = np.random.randint(25,50,(25,2))
>>> Y = np.random.randint(60,85,(25,2))
>>> Z = np.vstack((X,Y))
>>> # convert to np.float32
>>> Z = np.float32(Z)
>>> # define criteria and apply kmeans()
>>> criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 10, 1.0)
>>> ret,label,center=cv.kmeans(Z,2,None,criteria,10,cv.KMEANS_RANDOM_CENTERS)
>>> # Now separate the data, Note the flatten()
>>> A = Z[label.ravel()==0]
>>> B = Z[label.ravel()==1]
>>> # Plot the data
>>> plt.scatter(A[:,0],A[:,1])
>>> plt.scatter(B[:,0],B[:,1],c = 'r')
>>> plt.scatter(center[:,0],center[:,1],s = 80,c = 'y', marker = 's')
>>> plt.xlabel('Height'),plt.ylabel('Weight')
>>> plt.show()

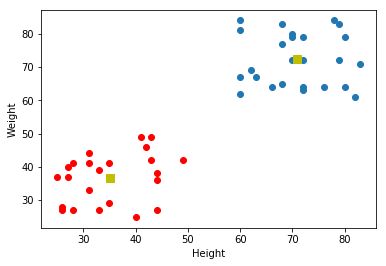
下面是我们得到的输出：

10.6.5. 三。色彩量化¶

颜色量化是减少图像中颜色数量的过程。这样做的一个原因是减少内存。有时，某些设备可能有限制，因此只能产生有限数量的颜色。在这些情况下，还执行颜色量化。这里我们使用k-均值聚类进行颜色量化。

这里没有什么新的解释。有3个特性，比如R，G，B。所以我们需要将图像重塑为Mx3大小的数组（M是图像中的像素数）。在聚类之后，我们将质心值（也就是R，G，B）应用于所有像素，这样得到的图像将具有指定数量的颜色。再次，我们需要重塑它回到原始图像的形状。下面是代码：

>>> import numpy as np
>>> import cv2 as cv
>>> img = cv.imread('/cvdata/home.jpg')
>>> Z = img.reshape((-1,3))
>>> # convert to np.float32
>>> Z = np.float32(Z)
>>> # define criteria, number of clusters(K) and apply kmeans()
>>> criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 10, 1.0)
>>> K = 8
>>> ret,label,center=cv.kmeans(Z,K,None,criteria,10,cv.KMEANS_RANDOM_CENTERS)
>>> # Now convert back into uint8, and make original image
>>> center = np.uint8(center)
>>> res = center[label.flatten()]
>>> res2 = res.reshape((img.shape))
>>>
>>> plt.imshow(res2)
>>>
>>> # cv.imshow('res2',res2)
>>> # cv.waitKey(0)
>>> # cv.destroyAllWindows()

<matplotlib.image.AxesImage at 0x7f224a830128>

K=8见下表：