原生晶体

备注

这些晶体中的每一个都将与任何Cartan矩阵输入一起工作(具有与给定Cartan矩阵对应的权重晶格中的权重)。

T形晶体

Let lambda be a weight. As defined in [Kashiwara1993] (see, also, [Kashiwara1995]) the crystal T_{lambda} = { t_{lambda} } is a single element crystal with the crystal structure defined by

\[\mathrm{wt}(t_\lambda) = \lambda, \quad e_i t_{\lambda} = f_i t_{\lambda} = 0, \quad \varepsilon_i(t_{\lambda}) = \varphi_i(t_{\lambda}) = -\infty.\]

The crystal T_{lambda} shifts the weights of the vertices in a crystal B by lambda when tensored with B, but leaves the graph structure of B unchanged. That is, for all b in B, we have mathrm{wt}(t_lambda otimes b) = mathrm{wt}(b) + lambda:

sage: B = crystals.Tableaux(['A',2],shape=[2,1])
sage: T = crystals.elementary.T(['A',2], B.Lambda()[1] + B.Lambda()[2])
sage: V = crystals.TensorProduct(T,B)
sage: for x in V:
....:     print(x.weight())
....:
(4, 2, 0)
(3, 3, 0)
(3, 2, 1)
(3, 1, 2)
(2, 2, 2)
(4, 1, 1)
(3, 2, 1)
(2, 3, 1)
sage: for x in B:
....:     print(x.weight() + T[0].weight())
....:
(4, 2, 0)
(3, 3, 0)
(3, 2, 1)
(3, 1, 2)
(2, 2, 2)
(4, 1, 1)
(3, 2, 1)
(2, 3, 1)

警告

Sage使用了与Kashiwara定义相反的张量积规则，因此在将这里的例子与Kashiwara的论文进行比较时必须小心。

以下是使用双曲Cartan矩阵的示例：

sage: A = CartanMatrix([[2,-4],[-4,2]])
sage: La = RootSystem(A).weight_lattice().fundamental_weights()
sage: La
Finite family {0: Lambda[0], 1: Lambda[1]}
sage: T = crystals.elementary.T(A,La[1])
sage: T
The T crystal of type [ 2 -4]
[-4  2] and weight Lambda[1]

C-晶体

定义于 [Kashiwara1993], 组元晶体 C = {c} 是单元素晶体，其晶体结构由

\[\mathrm{wt}(c) = 0, \quad e_i c = f_i c = 0, \quad \varepsilon_i(c) = \varphi_i(c) = 0.\]

注意事项 C cong B(0) ，在哪里 B(0) 是最重最重的水晶 0 。

The crystal C otimes T_mu is useful when finding subcrystals inside irreducible highest weight crystals B(lambda) where lambda is larger than mu in the lexicographic order. For example:

sage: P = RootSystem("C2").weight_lattice()
sage: La = P.fundamental_weights()
sage: h = P.simple_coroots()
sage: T = crystals.elementary.T("C2", 2*La[1])
sage: C = crystals.elementary.Component(P)
sage: B = crystals.TensorProduct(C,T)
sage: b = B(C[0],T[0])
sage: for i in B.index_set(): print(b.epsilon(i))
-2
0
sage: for i in B.index_set(): print(b.phi(i))
0
0
sage: for i in B.index_set(): print(b.f(i))
None
None
sage: for i in B.index_set(): print(b.e(i))
None
None

这种新晶体可以概括为下面的R-晶体。

R-晶体

For a fixed weight lambda, the crystal R_{lambda} = { r_{lambda} } is a single element crystal with the crystal structure defined by

\[\mathrm{wt}(r_{\lambda}) = \lambda, \quad e_i r_{\lambda} = f_i r_{\lambda} = 0, \quad \varepsilon_i(r_{\lambda}) = -\langle h_i, \lambda\rangle, \quad \varphi_i(r_{\lambda}) = 0,\]

哪里 {h_i} 就是那些简单的乌鸦。参见第146页 [Joseph1995], 例如，有关更多详细信息。(请注意，在 [Joseph1995], 这块水晶由 S_lambda 。)

张量 R_{lambda} 带着一颗水晶 B 会导致移动中顶点的权重 B 通过 lambda 并且还可以从原始图形中剪切出 B 。

警告

Sage使用了与Kashiwara定义相反的张量积规则，因此在将这里的例子与一些文献进行比较时必须小心。

For example, suppose mu le lambda in lexicographic ordering on weights, and one wants to see B(mu) as a subcrystal of B(lambda). Then B(mu) may be realized as the connected component of R_{mu-lambda}otimes B(lambda) containing the highest weight r_{mu-lambda} otimes u_lambda, where u_lambda is the highest weight vector in B(lambda):

sage: La = RootSystem(['B',4]).weight_lattice().fundamental_weights()
sage: Bla = crystals.NakajimaMonomials(['B',4], La[1]+La[2])
sage: Bmu = crystals.NakajimaMonomials(['B',4], La[1])
sage: R = crystals.elementary.R(['B',4], -La[2])
sage: T = crystals.TensorProduct(R,Bla)
sage: mg = mg = T(R[0], Bla.module_generators[0])
sage: S = T.subcrystal(generators=[mg])
sage: G = T.digraph(subset=S)
sage: Bmu.digraph().is_isomorphic(G, edge_labels=True)
True
sage: view(G, tightpage=True) # optional - dot2tex graphviz, not tested (opens external window)
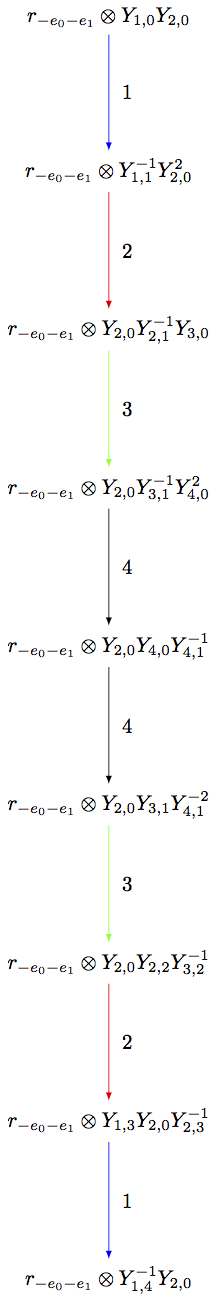
../_images/RmutensorBlambda.png

i -TH单晶

为 i 类型的索引集合中的元素 X ，水晶 B_i 类型的 X 是布景

\[B_i = \{ b_i(m) : m \in \ZZ \},\]

where the crystal structure is given by mathrm{wt}bigl(b_i(m)bigr) = malpha_i and

\[\begin{split}\begin{aligned} \varphi_j\bigl(b_i(m)\bigr) &= \begin{cases} m & \text{ if } j=i, \\ -\infty & \text{ if } j\neq i, \end{cases} & \varepsilon_j\bigl(b_i(m)\bigr) &= \begin{cases} -m & \text{ if } j=i, \\ -\infty & \text{ if } j\neq i, \end{cases} \\ f_j b_i(m) &= \begin{cases} b_i(m-1) & \text{ if } j=i, \\ 0 & \text{ if } j\neq i, \end{cases} & e_j b_i(m) &= \begin{cases} b_i(m+1) & \text{ if } j=i, \\ 0 & \text{ if } j\neq i. \end{cases} \end{aligned}\end{split}\]

看见 [Kashiwara1993] 或 [Kashiwara1995] 以获取更多信息。以下是一个示例：

sage: B = crystals.elementary.Elementary("A2",1)
sage: S = B.subcrystal(max_depth=4, generators=[B(0)])
sage: sorted(s for s in S)
[-4, -3, -2, -1, 0, 1, 2, 3, 4]
sage: G = B.digraph(subset=S)
sage: view(G, tightpage=True) # optional - dot2tex graphviz, not tested (opens external window)
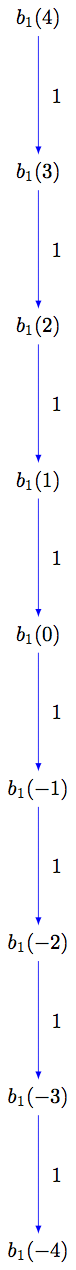
../_images/elementaryA2.png

警告

To reiterate, Sage uses the opposite convention for the tensor product rule to Kashiwara's definition. In particular, using Sage's convention, one has T_lambda otimes B_i cong B_i otimes T_{s_ilambda}, where s_i is the i-th simple reflection.