仿射最高重量晶体

仿射最高重量晶体是无限维的。它们的基本权格是包括零根的扩展权格 delta 。这与有限维仿射晶体形成对比，例如Kirillov-Reshetikhin晶体，其基本权重晶格是经典权重晶格，即不包括 delta 。

因此，要在Sage中使用它们，我们需要一些进一步的工具。

Littelmann路径模型

在Sage中实现了最高质量晶体的Littelmann路径模型。它模拟有限的最高晶体以及无限维的仿射最高重量晶体。晶体的元素是扩展的权重空间中的分段线性映射 QQ 。有关Littelmann路径模型的详细信息，请参阅 [L1995].

由于仿射的最高重量晶体是无限的，所以不可能列出所有元素或绘制整个晶体图。然而，如果用户只对离最高重量元素一定距离或深度的晶体感兴趣，则可以使用相应的亚晶体。要查看晶体的相应上部，可以构建关联的有向图：：

sage: R = RootSystem(['C',3,1])
sage: La = R.weight_space(extended = True).basis()
sage: LS = crystals.LSPaths(2*La[1]); LS
The crystal of LS paths of type ['C', 3, 1] and weight 2*Lambda[1]
sage: LS.weight_lattice_realization()
Extended weight space over the Rational Field of the Root system of type ['C', 3, 1]
sage: C = LS.subcrystal(max_depth=3)
sage: sorted(C, key=str)
[(-Lambda[0] + 2*Lambda[1] - Lambda[2] + Lambda[3] - delta, Lambda[1]),
 (-Lambda[0] + Lambda[1] + Lambda[2] - delta, Lambda[0] - Lambda[1] + Lambda[2]),
 (-Lambda[0] + Lambda[1] + Lambda[2] - delta, Lambda[1]),
 (-Lambda[1] + 2*Lambda[2] - delta, Lambda[1]),
 (2*Lambda[0] - 2*Lambda[1] + 2*Lambda[2],),
 (2*Lambda[1],),
 (Lambda[0] + Lambda[2] - Lambda[3], Lambda[1]),
 (Lambda[0] - Lambda[1] + Lambda[2], Lambda[1]),
 (Lambda[0] - Lambda[2] + Lambda[3], Lambda[0] - Lambda[1] + Lambda[2]),
 (Lambda[0] - Lambda[2] + Lambda[3], Lambda[1])]

sage: G = LS.digraph(subset = C)
sage: view(G, tightpage=True)  # optional - dot2tex graphviz, not tested (opens external window)
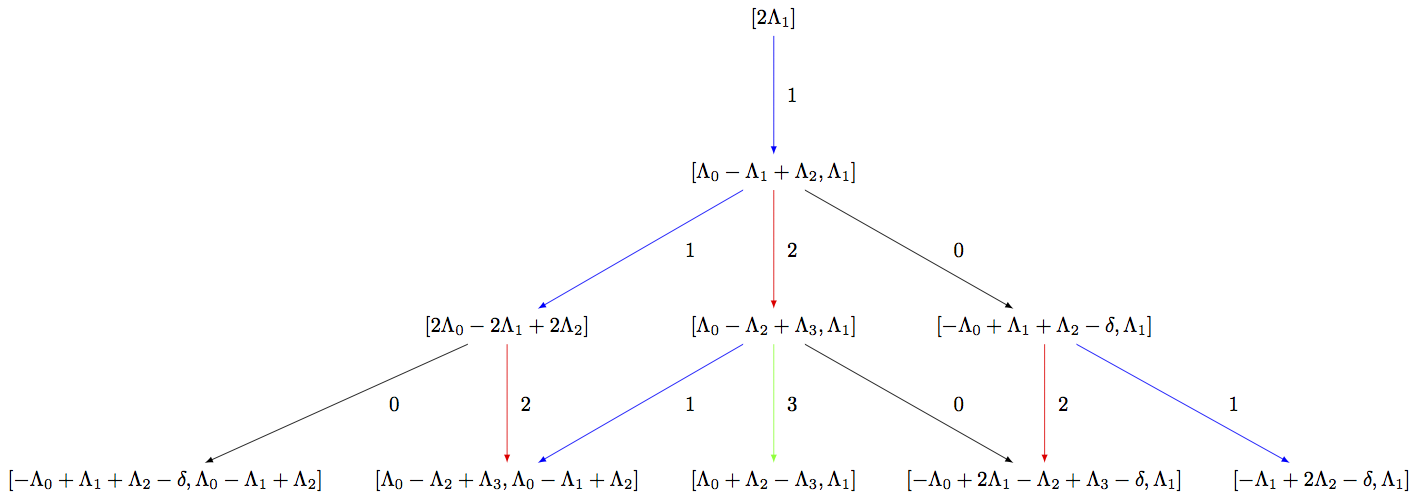
../_images/LScrystal.png

Littelmann路径模型也适合作为双无限零能级晶体的模型。要切割出这些晶体的切片，可以使用亚晶体中的方向选项：：

sage: R = RootSystem(['A',2,1])
sage: La = R.weight_space(extended = True).basis()
sage: LS = crystals.LSPaths(La[1]-La[0]); LS
The crystal of LS paths of type ['A', 2, 1] and weight -Lambda[0] + Lambda[1]
sage: C = LS.subcrystal(max_depth=2, direction='both')
sage: G = LS.digraph(subset = C)
sage: G.set_latex_options(edge_options=lambda uvl: ({}))
sage: view(G, tightpage=True)  # optional - dot2tex graphviz, not tested (opens external window)
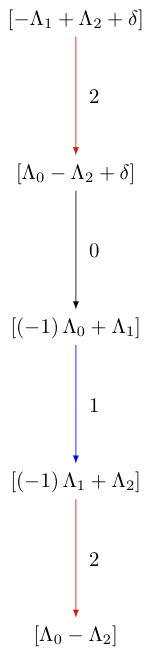
../_images/level_zero_crystal.png

修正Nakajima单项式

Modified Nakajima monomials have also been implemented in Sage. They model highest weight crystals in all symmetrizable types. The elements are given in terms of commuting variables Y_i(n) where i in I and n in ZZ_{geq 0}. For more information on the modified Nakajima monomials, see [KKS2007].

我们给出了一个仿射型的例子，并验证了直到深度3，它与Littelmann路径模型是一致的。与LS路径模型不同，Nakajima单项晶体由权重晶格(而不是权重空间)中的元素索引：

sage: La = RootSystem(['C',3,1]).weight_space(extended = True).fundamental_weights()
sage: LS = crystals.LSPaths(2*La[1]+La[2])
sage: SL = LS.subcrystal(max_depth=3)
sage: GL = LS.digraph(subset=SL)

sage: La = RootSystem(['C',3,1]).weight_lattice(extended = True).fundamental_weights()
sage: M = crystals.NakajimaMonomials(['C',3,1], 2*La[1]+La[2])
sage: SM = M.subcrystal(max_depth=3)
sage: GM = M.digraph(subset=SM)
sage: GL.is_isomorphic(GM, edge_labels=True)
True

现在我们做一个简单花边(因此可对称化)双曲线类型的例子 H_1^{(4)} ，它来自4个顶点上的完整图：：

sage: CM = CartanMatrix([[2, -1, -1,-1],[-1,2,-1,-1],[-1,-1,2,-1],[-1,-1,-1,2]]); CM
[ 2 -1 -1 -1]
[-1  2 -1 -1]
[-1 -1  2 -1]
[-1 -1 -1  2]
sage: La = RootSystem(CM).weight_lattice().fundamental_weights()
sage: M = crystals.NakajimaMonomials(CM, La[0])
sage: SM = M.subcrystal(max_depth=4)
sage: GM = M.digraph(subset=SM) # long time
../_images/hyperbolic_La0.png