经典晶体

经典晶体是来自有限(经典)类型的晶体。 A_r, B_r, C_r, D_r, E_{6,7,8}, F_4 ，以及 G_2 。在这里，我们先介绍一些背景知识，然后再进入晶体的一般理论和类型相关的组合学。

画面和表现形式 GL(n)

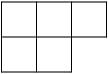
Let lambda be a partition. The Young diagram of lambda is the array of boxes having lambda_i boxes in the i-th row, left adjusted. Thus if lambda = (3, 2) the diagram is:

../_images/tableau1.png

A semi-standard Young tableau 形状的 lambda 是由行在微弱增加而列在严格增加的整数填充的框。因此，

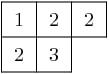
../_images/tableau2.png

是一个半标准的年轻画面。Sage有一个 Tableau 类，您可以按如下方式创建此画面：

sage: T = Tableau([[1,2,2], [2,3]]); T
[[1, 2, 2], [2, 3]]

A partition of length le r+1 is a dominant weight for GL(r+1, mathbf{C}) according to the description of the ambient space in 环境空间的标准实现. Therefore it corresponds to an irreducible representation pi_lambda = pi_lambda^{GL(r+1)} of GL(r+1, mathbf{C}).

It is true that not every dominant weight lambda is a partition, since a dominant weight might have some values lambda_i negative. The dominant weight lambda is a partition if and only if the character of lambda is a polynomial as a function on the space hbox{Mat}_n(mathbf{C}). Thus for example det^{-1} = pi_lambda with lambda = (-1, dots, -1), which is a dominant weight but not a partition, and the character is not a polynomial function on hbox{Mat}_n(mathbf{C}).

Theorem [Littlewood] If lambda is a partition, then the number of semi-standard Young tableaux with shape lambda and entries in {1,2,ldots,r+1} is the dimension of pi_lambda.

For example, if lambda = (3,2) and r = 2, then we find 15 tableaux with shape lambda and entries in {1,2,3}:

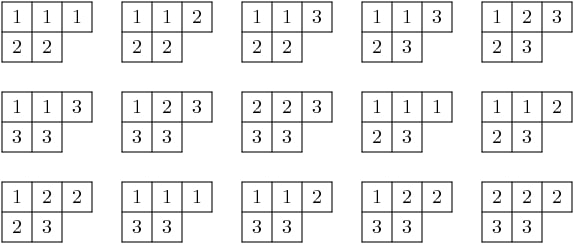
../_images/tableaux.png

这与定理是一致的，因为不可约表示的维度 GL(3) 具有最高权重的 (3,2,0) 尺寸为15：：

sage: A2 = WeylCharacterRing("A2")
sage: A2(3,2,0).degree()
15

In fact we may obtain the character of the representation from the set of tableaux. Indeed, one of the definitions of the Schur polynomial (due to Littlewood) is the following combinatorial one. If T is a tableaux, define the weight of T to be hbox{wt}(T) = (k_1,dots,k_n) where k_i is the number of i's in the tableaux. Then the multiplicity of mu in the character chi_lambda is the number of tableaux of weight lambda. Thus if mathbf{z} = (z_1,dots,z_n), we have

\[\chi_\lambda(\mathbf{z}) = \sum_T \mathbf{z}^{\hbox{wt}(T)}\]

where the sum is over all semi-standard Young tableaux of shape lambda that have entries in {1, 2, ldots, r+1}.

Frobenius-Schur二元性

Frobenius-Schur对偶是对称群的表示理论与一般线性群的表示理论之间的一种关系。我们将在下一节中将这一点与场景相关联。

Representations of the symmetric group S_k are parametrized by partitions lambda of k. The parametrization may be characterized as follows. Let n be any integer ge k. Then both GL(n,mathbf{C}) and S_k act on otimes^k V where V = mathbf{C}^n. Indeed, GL(n) acts on each V and S_k permutes them. Then if pi_lambda^{GL(n)} is the representation of GL(n,mathbf{C}) with highest weight vector lambda and pi_lambda^{S_k} is the irreducible representation of S_k parametrized by lambda then

\[\otimes^k V \cong \bigoplus_{\lambda\vdash k}\pi^{GL(n)}_\lambda\otimes\pi^{S_k}_\lambda\]

作为两组的双模。这是 Frobenius-Schur duality 并且它用来刻画不可约表示的参数化。 S_k 通过以下分区 k 。

计算成对的画面

在这两种表征理论中， GL(n) 和表象理论 S_k ，不可约表示的次数可以用适当类型的表的个数来表示。我们已经陈述了以下定理 GL(n) 。为 S_k ，它是这样的。

让我们假设一个半标准的Young画面 T 形状的 lambdavdash k 是 standard 如果 T 包含每个条目 1,2,dots,k 只有一次。因此，行和列都在严格增加。

Theorem [Young, 1927] The degree of pi_lambda is the number of standard tableaux of shape lambda.

Now let us consider the implications of Frobenius-Schur duality. The dimension of otimes^k V is n^k. Therefore n^k is equal to the number of pairs (T1,T2) of tableaux of the same shape lambdavdash k, where the first tableaux is standard (in the alphabet 1,2,ldots,k), and the second the second semistandard (in the alphabet 1,2,ldots,n).

Robinson-Schensted-Knuth对应

最后一个纯组合陈述有一个基于Robinson-Schensted-Knuth(RSK)对应的组合证明。

参考资料：

RSK对应给出了不同类型的画面对和不同类型的组合对象之间的双射。我们不会在这里详细查看通信，但请参阅参考资料。我们注意到，Schensted插入被实现为方法 schensted_insertion 在塞奇的Tableau班级。

因此，我们有以下两个猜想：

  • Pairs of tableaux T_1 and T_2 of shape lambda where lambda runs through the partitions of k such that T_1 is a standard tableau and T_2 is a semistandard tableau in 1,2,dots,n are in bijection with the n^k words of length k in 1,2,dots,n.

  • 两对相同形状的标准画面 lambda AS lambda 贯穿所有分区 k 都与 k! 元素： S_k 。

  • 成对的场面 T_1 和 T_2 形状相同的 lambda 但任意大小的 1,2,3,dots,n 与……存在着矛盾 n times n 正整数矩阵。

  • 成对的场面 T_1 和 T_2 共轭形状的 lambda 和 lambda' 与……存在着矛盾 n times n 带条目的矩阵 0 或 1 。

The second of these four bijection gives a combinatorial proof of the fact explained above, that the number of pairs (T1,T2) of tableaux of the same shape lambdavdash k, where the first tableaux is standard (in the alphabet 1,2,cdots,k), and the second the second semistandard (in the alphabet 1,2,cdots,n). So this second bijection is a combinatorial analog of Frobenius-Schur duality.

表示论与组合学之间的类比

上面引用的四个组合双射(RSK的变体)在表示理论中有以下相似之处。

  • 第一个组合事实对应于Frobenius-Schur对偶，正如我们已经解释过的。

  • The second combinatorial fact also has an analog in representation theory. The group algebra mathbf{C}[S_k] is an S_k times S_k bimodule with of dimension k!. It decomposes as a direct sum of pi_lambda^{S_k} otimes pi_lambda^{S_k}.

无论是组合事实还是分解 mathbf{C}[S_k] 显示标准画面的大小对的数量 k 同样的形状等于 k! 。

  • The third combinatorial fact is analogous to the decomposition of the ring of polynomial functions on hbox{Mat}(n, mathbf{C}) on which GL(n, mathbf{C}) times GL(n, mathbf{C}) acts by (g_1, g_2)f(X) = f({^t g_1}X g_2). The polynomial ring decomposes into the direct sum of pi^{GL(n)}_lambda otimes pi^{GL(n)}_lambda.

跟踪会给你带来 Cauchy identity ：

\[\sum_\lambda s_\lambda(x_1,\cdots,x_n) s_\lambda(y_1,\cdots,y_n) =\prod_{i,j}(1-x_i y_j)^{-1}\]

哪里 x_i 是的特征值 g_1 和 y_j 是的特征值 g_2 。总和是所有分区的总和 lambda 。

  • 最后一个组合事实类似于外代数在上的分解。 hbox{Mat}(n, mathbf{C}) 。

跟踪会给你带来 dual Cauchy identity ：

\[\sum_\lambda s_\lambda(x_1,\cdots,x_n) s_{\lambda'}(y_1,\cdots,y_n) =\prod_{i,j}(1+x_i y_j).\]

总和再一次超过了分区 lambda 还有这里 lambda' 是共轭分割。

表现论与组合学之间的插补

The theory of quantum groups interpolates between the representation theoretic picture and the combinatorial picture, and thereby explains these analogies. The representation pi_lambda^{GL(n)} is reinterpreted as a module for the quantized enveloping algebra U_q(mathfrak{gl}_n(mathbf{C})), and the representation pi_lambda^{S_k} is reinterpreted as a module for the Iwahori Hecke algebra. Then Frobenius-Schur duality persists. See [Jimbo1986]. When q to 1, we recover the representation story. When q to 0, we recover the combinatorial story.

柏原水晶

参考资料：

Kashiwara认为量子化包络代数的最高权模 U_q(mathfrak{g}) 在限制的时候 q to 0 。在以下情况下不能定义包络代数 q = 0 ，但仍可检测到限制结构。这是 crystal basis 该模块的。

鹿原的晶体碱具有一种组合结构，甚至可以揭示早于量子群的台面上的纯组合结构。它很好地推广了其他Cartan类型(或者更一般地推广到Kac-Moody代数)。

Let Lambda be the weight lattice of a Cartan type with root system Phi. We now define a crystal of type Phi. Let mathcal{B} be a set, and let 0 notin mathcal{B} be an auxiliary element. For each index 1 le i le r we assume there given maps e_i, f_i : mathcal{B} longrightarrow mathcal{B} cup {0}, maps varepsilon_i, varphi_i : mathcal{B} longrightarrow mathbf{Z} and a map hbox{wt} : mathcal{B} longrightarrow Lambda satisfying certain assumptions, which we now describe. It is assumed that if x, y in mathcal{B} then e_i (x) = y if and only if f_i (y) = x. In this case, it is assumed that

\[\hbox{wt} (y) = \hbox{wt} (x) + \alpha_i, \qquad \varepsilon_i (x) = \varepsilon_i (y) + 1, \qquad \varphi_i (x) = \varphi_i (y) - 1.\]

此外，我们假设

\[\varphi_i (x) - \varepsilon_i (x) = \left\langle \hbox{wt} (x), \alpha^{\vee}_i \right\rangle\]

为了所有人 x in mathcal{B} 。

We call a crystal regular if it satisfies the additional assumption that varepsilon_i(v) is the number of times that e_i may be applied to v, and that phi_i(v) is the number of times that f_i may be applied. That is, varphi_i (x) = max {k | f_i^k x neq 0} and varepsilon_i (x) = max {k | e_i^k (x) neq 0}. Kashiwara also allows varepsilon_i and varphi_i to take the value -infty.

备注

我们在这里关注的大多数晶体都是规则的。

给出了水晶 mathcal{B} vt.的. character chi_{mathcal{B}} 是：

\[\sum_{v\in\mathcal{B}} {\mathbf{z}}^{wt(v)}.\]

Given any highest weight lambda, constructions of Kashiwara and Nakashima, Littelmann and others produce a crystal chi_{mathcal{B}_lambda} such that chi_{mathcal{B}_lambda} = chi_lambda, where chi_lambda is the irreducible character with highest weight lambda, as in 表象和人物.

The crystal mathcal{B}_lambda is not uniquely characterized by the properties that we have stated so far. For Cartan types A, D, E (more generally, any simply-laced type) it may be characterized by these properties together with certain other Stembridge axioms. We will take it for granted that there is a unique "correct" crystal mathcal{B}_lambda and discuss how these are constructed in Sage.

正在安装dot2tex

在给出水晶的例子之前，我们离题来帮助您安装 dot2tex ，你将需要它来制作水晶的 Latex 图像。

dot2tex 是SAGE的可选程序包，可通过以下方式安装最新版本：

$ sage -i dot2tex

这也需要各种 Latex 包装。以下命令会检查这些选项是否可用：

sage: from sage.graphs.graph_latex import check_tkz_graph
sage: check_tkz_graph() # random

Sage中的tableaux报表

当前在Sage中的所有晶体都可以通过 crystals.<tab> 。

For type A_r, Kashiwara and Nakashima put a crystal structure on the set of tableaux with shape lambda in 1, 2, ldots, r+1, and this is a realization of mathcal{B}_{lambda}. Moreover, this construction extends to other Cartan types, as we will explain. At the moment, we will consider how to draw pictures of these crystals.

一旦你有了 dot2tex 安装后，您可以使用如下命令制作水晶的图像图片：：

sage: fn = tmp_filename(ext=".tex")
sage: crystals.Tableaux("A2", shape=[2,1]).latex_file(fn)

Here lambda = (2,1)=(2,1,0). The crystal C is mathcal{B}_{lambda}. The character chi_lambda will therefore be the eight-dimensional irreducible character with this highest weight. Then you may run pdflatex on the file a2rho.tex. This can also be achieved without the detour of saving the latex file via:

sage: B = crystals.Tableaux(['A',2], shape=[2,1])
sage: view(B, tightpage=True) # optional - dot2tex graphviz, not tested (opens external window)

这将生成水晶图：

../_images/a2rho_color.png

您可能还希望通过指定其他 Latex 选项来为边缘添加不同的颜色：

sage: B = crystals.Tableaux(['A',2], shape=[2,1])
sage: G = B.digraph()
sage: G.set_latex_options(color_by_label = {1:"red", 2:"yellow"})
sage: view(G, tightpage=True) # optional - dot2tex graphviz, not tested (opens external window)

As you can see, the elements of this crystal are exactly the eight tableaux of shape lambda with entries in {1,2,3}. The convention is that if x,y in mathcal{B} and f_i(x) = y, or equivalently e_i(y) = x, then we draw an arrow from x to y. Thus the highest weight tableau is the one with no incoming arrows. Indeed, this is:

\[\]
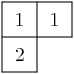
../_images/tableau3.png

我们记得画面的份量是 (k_1,k_2,k_3) 哪里 k_i 是指 i 在画面中，所以这个画面很有份量 (2,1,0) ，这确实等于 lambda 。

创建晶体后，您可以通过该方法访问环境空间及其方法 weight_lattice_realization() **

sage: C = crystals.Tableaux("A2", shape=[2,1])
sage: L = C.weight_lattice_realization(); L
Ambient space of the Root system of type ['A', 2]
sage: L.fundamental_weights()
Finite family {1: (1, 0, 0), 2: (1, 1, 0)}

最高权重向量如下所示：

sage: C = crystals.Tableaux("A2", shape=[2,1])
sage: v = C.highest_weight_vector(); v
[[1, 1], [2]]

或者更简单：：

sage: C = crystals.Tableaux("A2", shape=[2,1])
sage: C[0]
[[1, 1], [2]]

现在我们可以应用运算符 e_i 和 f_i 要在水晶中四处移动：：

sage: C = crystals.Tableaux("A2", shape=[2,1])
sage: v = C.highest_weight_vector()
sage: v.f(1)
[[1, 2], [2]]
sage: v.f(1).f(1)
sage: v.f(1).f(1) is None
True
sage: v.f(1).f(2)
[[1, 3], [2]]
sage: v.f(1).f(2).f(2)
[[1, 3], [3]]
sage: v.f(1).f(2).f(2).f(1)
[[2, 3], [3]]
sage: v.f(1).f(2).f(2).f(1) == v.f(2).f(1).f(1).f(2)
True

如果首先制作一个Weyl角色环：：，则可以构造角色

sage: A2 = WeylCharacterRing("A2")
sage: C = crystals.Tableaux("A2", shape=[2,1])
sage: C.character(A2)
A2(2,1,0)

字母的水晶

对于每个经典的Cartan类型，都有一个 standard crystal mathcal{B}_{hbox{standard}} 通过取张量积和提取组成的不可约晶体，可以从这些晶体中建立起其他晶体。此过程对Cartan类型已足够 A_r 和 C_r 。对于类型 B_r 和 D_r 标准晶体必须添加 spin crystals 。看见 [KashiwaraNakashima1994] 或 [HongKang2002] 了解更多细节。

这是一种典型的标准水晶 A_r 。

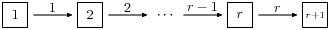
../_images/stand-a.png

您可以创建水晶并使用它，如下所示：

sage: C = crystals.Letters("A6")
sage: v0 = C.highest_weight_vector(); v0
1
sage: v0.f(1)
2
sage: v0.f(1).f(2)
3
sage: [v0.f(1).f(2).f(x) for x in [1..6]]
[None, None, 4, None, None, None]
sage: [v0.f(1).f(2).e(x) for x in [1..6]]
[None, 2, None, None, None, None]

这是一种典型的标准水晶 B_r 。

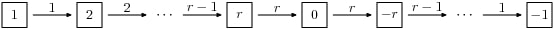
../_images/stand-b.png

There is, additionally, a spin crystal for B_r, corresponding to the 2^r-dimensional spin representation. We will not draw it, but we will describe it. Its elements are vectors epsilon_1otimescdotsotimesepsilon_r, where each spin epsilon_i=pm.

If i<r, then the effect of the operator f_i is to annihilate v = epsilon_1 otimes cdots otimes epsilon_r unless epsilon_i otimes epsilon_{i+1} = + otimes -. If this is so, then f_i(v) is obtained from v by replacing epsilon_i otimes epsilon_{i+1} by - otimes +. If i=r, then f_r annihilates v unless epsilon_r=+, in which case it replaces epsilon_r by -.

创建旋转晶体，如下所示。晶体元素在签名表示中表示，列出 epsilon_i **

sage: C = crystals.Spins("B3")
sage: C.list()
[+++, ++-, +-+, -++, +--, -+-, --+, ---]

这是一种典型的标准水晶 C_r 。

../_images/stand-c.png

这是一种典型的标准水晶 D_r 。

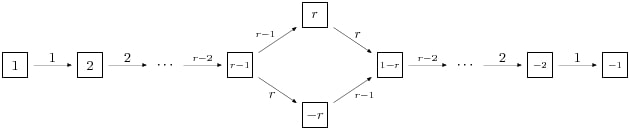
../_images/stand-d.png

There are two spin crystals for type D_r. Each consists of epsilon_1 otimes cdots otimes epsilon_r with epsilon_i = pm, and the number of spins either always even or always odd. We will not describe the effect of the root operators f_i, but you are invited to create them and play around with them to guess the rule:

sage: Cplus = crystals.SpinsPlus("D4")
sage: Cminus = crystals.SpinsMinus("D4")

也有可能为类型构造标准晶体 G_2 ， E_6 ，以及 E_7 。这就是打字用的 G_2 (对应于阶数7的表示法)：

../_images/stand-g.png

字母水晶是画面水晶的特例，从这个意义上说 mathcal{B}_{hbox{standard}} 与其最大重量的画面晶体同构 lambda 是标准表示形式的最高权重向量。因此，请比较：

sage: crystals.Letters("A3")
The crystal of letters for type ['A', 3]
sage: crystals.Tableaux("A3", shape=[1])
The crystal of tableaux of type ['A', 3] and shape(s) [[1]]

这两个晶体在实现上不同，但它们是同构的。事实上，第二个晶体是由第一个晶体构成的。我们可以测试晶体之间的同构，如下所示：

sage: Cletter = crystals.Letters(['A',3])
sage: Ctableaux = crystals.Tableaux(['A',3], shape = [1])
sage: Cletter.digraph().is_isomorphic(Ctableaux.digraph())
True
sage: Cletter.digraph().is_isomorphic(Ctableaux.digraph(), certificate = True)
(True, {1: [[1]], 2: [[2]], 3: [[3]], 4: [[4]]})

在最后一步中，给出了晶体顶点之间的显式映射。

字母晶体在这一理论中具有特殊的作用，因为它们特别简单，但正如鹿原和中岛所展示的那样，可以用它们来创造画面的晶体。我们将回顾这是如何运作的。

晶体的张量积

Kashiwara defined the tensor product of crystals in a purely combinatorial way. The beauty of this construction is that it exactly parallels the tensor product of crystals of representations. That is, if lambda and mu are dominant weights, then mathcal{B}_lambda otimes mathcal{B}_mu is a (usually disconnected) crystal, which may contain multiple copies of mathcal{B}_nu (for another dominant weight nu), and the number of copies of mathcal{B}_nu is exactly the multiplicity of chi_nu in chi_lambda chi_mu.

我们将描述晶体张量积的两个约定。

柏原的定义

As a set, the tensor product mathcal{B} otimes mathcal{C} of crystals mathcal{B} and mathcal{C} is the Cartesian product, but we denote the ordered pair (x, y) with x in mathcal{B} and y in mathcal{C} by x otimes y. We define hbox{wt} (x otimes y) = hbox{wt} (x) + hbox{wt}(y). We define

\[\begin{split}f_i (x \otimes y) = \begin{cases} f_i (x) \otimes y & \text{if $\varphi_i (x) > \varepsilon_i (y)$},\\ x \otimes f_i (y) & \text{if $\varphi_i (x) \le \varepsilon_i (y)$}, \end{cases}\end{split}\]

和

\[\begin{split}e_i (x \otimes y) = \begin{cases} e_i (x) \otimes y & \text{if $\varphi_i (x) \ge \varepsilon_i (y)$},\\ x \otimes e_i (y) & \text{if $\varphi_i (x) < \varepsilon_i (y)$}. \end{cases}\end{split}\]

据了解， x otimes 0 = 0 otimes x = 0 。我们还定义了：

\[\varphi_i (x \otimes y) = \max (\varphi_i (y), \varphi_i (x) + \varphi_i (y) - \varepsilon_i (y)),\]
\[\varepsilon_i (x \otimes y) = \max (\varepsilon_i (x), \varepsilon_i (x) + \varepsilon_i (y) - \varphi_i (x)) .\]

备选定义

As a set, the tensor product mathcal{B} otimes mathcal{C} of crystals mathcal{B} and mathcal{C} is the Cartesian product, but we denote the ordered pair (y, x) with y in mathcal{B} and x in mathcal{C} by x otimes y. We define hbox{wt} (x otimes y) = hbox{wt} (y) + hbox{wt}(x). We define

\[\begin{split}f_i (x \otimes y) = \begin{cases} f_i (x) \otimes y & \text{if $\varphi_i (y) \le \varepsilon_i (x)$},\\ x \otimes f_i (y) & \text{if $\varphi_i (y) > \varepsilon_i (x)$}, \end{cases}\end{split}\]

和

\[\begin{split}e_i (x \otimes y) = \begin{cases} e_i (x) \otimes y & \text{if $\varphi_i (y) < \varepsilon_i (x)$},\\ x \otimes e_i (y) & \text{if $\varphi_i (y) \ge \varepsilon_i (x)$}. \end{cases}\end{split}\]

据了解， y otimes 0 = 0 otimes y = 0 。我们还定义了

\[\varphi_i (x \otimes y) = \max (\varphi_i (x), \varphi_i (y) + \varphi_i (x) - \varepsilon_i (x)),\]
\[\varepsilon_i (x \otimes y) = \max (\varepsilon_i (y), \varepsilon_i (y) + \varepsilon_i (x) - \varphi_i (y)).\]

The tensor product is associative: (x otimes y) otimes z mapsto x otimes(y otimes z) is an isomorphism (mathcal{B} otimes mathcal{C}) otimes mathcal{D} to mathcal{B} otimes (mathcal{C} otimes mathcal{D}), and so we may consider tensor products of arbitrary numbers of crystals.

两种定义之间的关系

The relationship between the two definitions is simply that the Kashiwara tensor product mathcal{B} otimes mathcal{C} is the alternate tensor product mathcal{C} otimes mathcal{B} in reverse order. Sage uses the alternative tensor product. Even though the tensor product construction is a priori asymmetrical, both constructions produce isomorphic crystals, and in particular Sage's crystals of tableaux are identical to Kashiwara's.

备注

Using abstract crystals (i.e. they satisfy the axioms but do not arise from a representation of U_q(mathfrak{g})), we can construct crystals mathcal{B}, mathcal{C} such that mathcal{B} otimes mathcal{C} neq mathcal{C} otimes mathcal{B} (of course, using the same convention).

Sage中晶体的张量积

你可以在Sage中构造几个晶体的张量积，使用 crystals.TensorProduct **

sage: C = crystals.Letters("A2")
sage: T = crystals.TensorProduct(C,C,C); T
Full tensor product of the crystals [The crystal of letters for type ['A', 2],
The crystal of letters for type ['A', 2], The crystal of letters for type ['A', 2]]
sage: T.cardinality()
27
sage: T.highest_weight_vectors()
([1, 1, 1], [2, 1, 1], [1, 2, 1], [3, 2, 1])

这个水晶有四个最高的重量向量。我们可以这样理解：

sage: A2 = WeylCharacterRing("A2")
sage: C = crystals.Letters("A2")
sage: T = crystals.TensorProduct(C,C,C)
sage: chi_C = C.character(A2)
sage: chi_T = T.character(A2)
sage: chi_C
A2(1,0,0)
sage: chi_T
A2(1,1,1) + 2*A2(2,1,0) + A2(3,0,0)
sage: chi_T == chi_C^3
True

As expected, the character of T is the cube of the character of C, and representations with highest weight (1,1,1), (3,0,0) and (2,1,0). This decomposition is predicted by Frobenius-Schur duality: the multiplicity of pi_lambda^{GL(n)} in otimes^3mathbf{C}^3 is the degree of pi_lambda^{S_3}.

能够选择一个不可约的组份是有用的 T 。如果我们只想要一个不可还原的成分 T ，我们可以通过选项指定最高权重向量的列表 generators 。如果列表只有一个元素，那么我们得到一个不可约的晶体。我们可以制造四个这样的晶体：

sage: A2 = WeylCharacterRing("A2")
sage: C = crystals.Letters("A2")
sage: T = crystals.TensorProduct(C,C,C)
sage: [T1,T2,T3,T4] = \
  [crystals.TensorProduct(C,C,C,generators=[v]) for v in T.highest_weight_vectors()]
sage: [B.cardinality() for B in [T1,T2,T3,T4]]
[10, 8, 8, 1]
sage: [B.character(A2) for B in [T1,T2,T3,T4]]
[A2(3,0,0), A2(2,1,0), A2(2,1,0), A2(1,1,1)]

我们看到其中两个晶体是同构的，有特征 A2(2,1,0) 。尝试：：

sage: A2 = WeylCharacterRing("A2")
sage: C = crystals.Letters("A2")
sage: T = crystals.TensorProduct(C,C,C)
sage: [T1,T2,T3,T4] = \
  [crystals.TensorProduct(C,C,C,generators=[v]) for v in T.highest_weight_vectors()]
sage: T1.plot()
Graphics object consisting of 35 graphics primitives
sage: T2.plot()
Graphics object consisting of 25 graphics primitives
sage: T3.plot()
Graphics object consisting of 25 graphics primitives
sage: T4.plot()
Graphics object consisting of 2 graphics primitives

Elements of crystals.TensorProduct(A,B,C, ...) are represented by sequences [a,b,c, ...] with a in A, b in B, etc. This of course represents a otimes b otimes c otimes cdots.

作为晶体张量积的Tableaux晶体

Sage实现了 CrystalOfTableaux 作为张量积的子晶 ClassicalCrystalOfLetters 。您可以看到它是如何完成的，如下所示：

sage: T = crystals.Tableaux("A4",shape=[3,2])
sage: v = T.highest_weight_vector().f(1).f(2).f(3).f(2).f(1).f(4).f(2).f(3); v
[[1, 2, 5], [3, 4]]
sage: list(v)
[3, 1, 4, 2, 5]

我们已经查看了内部表示 v 的四次张量次方的元素来表示 ClassicalCrystalOfLetters 。我们看到画面：

\[\]
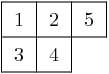
../_images/tableau4.png

被解释为张量：

\[\]
../_images/tensor.png

画面的元素从下到上，从左到右阅读。这是 inverse middle-Eastern reading 在画面上。见洪和康， loc. cit. 讨论画面的读数。

自旋晶体

对于Cartan类型的 A_r ， C_r 或 G_2 ， CrystalOfTableaux 能够制造出任何有限的晶体。(对于类型 A_r 有必要将最高的重量 lambda 成为一个分区。)

对于Cartan类型 B_r 和 D_r ，也存在自旋表示。相应的晶体实现为 spin crystals 。对于这些类型， CrystalOfTableaux 还允许输入形状 lambda 如果它是高度的，则是半积分的 r 。例如：：

sage: C = crystals.Tableaux(['B',2], shape = [3/2, 1/2])
sage: C.list()
[[++, [[1]]], [++, [[2]]], [++, [[0]]], [++, [[-2]]], [++, [[-1]]], [+-, [[-2]]],
[+-, [[-1]]], [-+, [[-1]]], [+-, [[1]]], [+-, [[2]]], [-+, [[2]]], [+-, [[0]]],
[-+, [[0]]], [-+, [[-2]]], [--, [[-2]]], [--, [[-1]]]]

Here the first list of + and - gives a spin column that is discussed in more detail in the next section and the second entry is a crystal of tableau element for lambda = (lfloor lambda_1 rfloor, lfloor lambda_2 rfloor, ldots ). For type D_r, we have the additional feature that there are two types of spin crystals. Hence in CrystalOfTableaux the r-th entry of lambda in this case can also take negative values:

sage: C = crystals.Tableaux(['D',3], shape = [1/2, 1/2,-1/2])
sage: C.list()
[[++-, []], [+-+, []], [-++, []], [---, []]]

对于排名第二的Cartan类型，我们也有 crystals.FastRankTwo 这为这些晶体提供了不同的快速实现：

sage: B = crystals.FastRankTwo(['B',2], shape=[3/2,1/2]); B
The fast crystal for B2 with shape [3/2,1/2]
sage: v = B.highest_weight_vector(); v.weight()
(3/2, 1/2)

B型自旋晶体

自旋晶体具有最高的重量 (1/2,dots,1/2) 。这是最后一个基本权重。具有这个权重的不可约表示是度的自旋表示 2^r 。它的水晶用Sage：：手工编码。

sage: Cspin = crystals.Spins("B3"); Cspin
The crystal of spins for type ['B', 3]
sage: Cspin.cardinality()
8

The crystals with highest weight lambda, where lambda is a half-integral weight, are constructed as a tensor product of a spin column and the highest weight crystal of the integer part of lambda. For example, suppose that lambda = (3/2, 3/2, 1/2). The corresponding irreducible character will have degree 112:

sage: B3 = WeylCharacterRing("B3")
sage: B3(3/2,3/2,1/2).degree()
112

So mathcal{B}_lambda will have 112 elements. We can find it as a subcrystal of Cspin otimes mathcal{B}_mu, where mu = lambda-(1/2,1/2,1/2) = (1,1,0):

sage: B3 = WeylCharacterRing("B3")
sage: B3(1,1,0)*B3(1/2,1/2,1/2)
B3(1/2,1/2,1/2) + B3(3/2,1/2,1/2) + B3(3/2,3/2,1/2)

我们看到，只要取这两个晶体的张量积，就会产生一个有三个组分的可约晶体，我们想要提取我们想要的那个。我们的做法如下：

sage: B3 = WeylCharacterRing("B3")
sage: C1 = crystals.Tableaux("B3", shape=[1,1])
sage: Cspin = crystals.Spins("B3")
sage: C = crystals.TensorProduct(C1, Cspin, generators=[[C1[0],Cspin[0]]])
sage: C.cardinality()
112

或者，我们可以直接从 CrystalOfTableaux **

sage: C = crystals.Tableaux(['B',3], shape = [3/2,3/2,1/2])
sage: C.cardinality()
112

这就是我们想要的水晶。

D型自旋晶体

类似的情况也适用于文字 D_r ，但现在有两个自旋晶体，都是程度不同的 2^{r-1} 。这些代码在SAGE中手工编码：：

sage: SpinPlus = crystals.SpinsPlus("D4")
sage: SpinMinus = crystals.SpinsMinus("D4")
sage: SpinPlus[0].weight()
(1/2, 1/2, 1/2, 1/2)
sage: SpinMinus[0].weight()
(1/2, 1/2, 1/2, -1/2)
sage: [C.cardinality() for C in [SpinPlus,SpinMinus]]
[8, 8]

与B型晶体类似，我们通过允许具有半整数值的分区来获得具有自旋重量的晶体，最后一项可以是负值，这取决于自旋的类型。

Lusztig对合

The Lusztig involution on a finite-dimensional highest weight crystal B(lambda) of highest weight lambda maps the highest weight vector to the lowest weight vector and the Kashiwara operator f_i to e_{i^*}, where i^* is defined as alpha_{i^*} = -w_0(alpha_i). Here w_0 is the longest element of the Weyl group acting on the i-th simple root alpha_i. For example, for type A_n we have i^*=n+1-i, whereas for type C_n we have i^*=i. For type D_n and n even also have i^*=i, but for n odd this map interchanges nodes n-1 and n. Here is how to achieve this in Sage:

sage: B = crystals.Tableaux(['A',3],shape=[2,1])
sage: b = B(rows=[[1,2],[3]])
sage: b.lusztig_involution()
[[2, 4], [3]]

对于类型 A_n ，Lusztig对合与Schuetzenberger对合(在Sage中定义在Tableaux上)相同：

sage: t = Tableau([[1,2],[3]])
sage: t.schuetzenberger_involution(n=4)
[[2, 4], [3]]

对于给定晶体中的所有画面，可以通过以下方式进行测试：

sage: B = crystals.Tableaux(['A',3],shape=[2])
sage: all(b.lusztig_involution().to_tableau() == b.to_tableau().schuetzenberger_involution(n=4) for b in B)
True

对于特殊类型的有限维最高重量晶体，也定义了Lusztig对合：

sage: C = CartanType(['E',6])
sage: La = C.root_system().weight_lattice().fundamental_weights()
sage: T = crystals.HighestWeight(La[1])
sage: t = T[4]; t
[(-2, 5)]
sage: t.lusztig_involution()
[(-3, 2)]

晶体的Levi分枝规则

让我们 G 做一个李群 H 李维亚群。我们已经看到了动态金图 H 是从以下内容获得的 G 通过擦除一个或多个节点。

如果 mathcal{C} 是一颗水晶 G ，那么我们就可以得到相应的晶体 H 通过类似的过程。例如，如果动态金图 H 是从动态金图中获得的 G 通过擦除 i -第1个节点，那么如果我们擦除晶体中的所有边 mathcal{C} 它们都标有 i ，我们得到了一个晶体， H 。

在Sage中，这是通过指定在有向图方法中使用的索引集来实现的：

sage: T = crystals.Tableaux(['D',4],shape=[1])
sage: G = T.digraph(index_set=[1,2,3])

我们看到，这种类型 D_4 晶体确实分解成两种类型 A_3 组件。

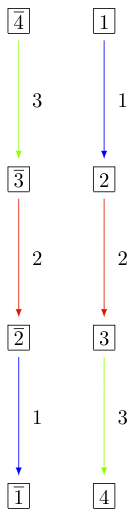
../_images/parabolic_subcrystal.png

有关分支规则的详细信息，请参阅 极大子群与分枝规则 或 Levi子群 有关Levi亚群的详细信息。

亚晶

有时，可能需要处理晶体的亚晶体。例如，人们可能想要查看所有 {2,3,ldots,n} 晶体的最高元素，并查看特定的此类成分：：

sage: T = crystals.Tableaux(['D',4],shape=[2,1])
sage: hw = [ t for t in T if t.is_highest_weight(index_set = [2,3,4]) ]; hw
[[[1, 1], [2]],
 [[1, 2], [2]],
 [[2, -1], [-2]],
 [[2, -1], [-1]],
 [[1, -1], [2]],
 [[2, -1], [3]],
 [[1, 2], [3]],
 [[2, 2], [3]],
 [[1, 2], [-2]],
 [[2, 2], [-2]],
 [[2, 2], [-1]]]
sage: C = T.subcrystal(generators = [T(rows=[[2,-1],[3]])], index_set = [2,3,4])
sage: G = T.digraph(subset = C, index_set=[2,3,4])