李群基础¶
本节的目标¶
因为我们在这里必须简短,所以这不是一个真正学习李群或李代数的地方。相反,这一节的重点是概述您需要了解哪些知识才能有效地使用Sage进行测谎计算,并确定想法和符号。
半单群和约化群¶
如果 g in GL(n,CC) ,那么 g 可以被唯一地分解为 g_1 g_2 哪里 g_1 和 g_2 通勤,与 g_1 半单(可对角化)和 g_2 幂等(它的所有特征值都等于1)。这源于约旦河的规范形式。如果 g = g_1 然后 g 名为 semisimple 如果 g = g_2 然后 g 名为 unipotent 。
我们认为李群 G 和一类表示,如果一个元素 g in G 是一元性的(分别是半单)在来自类的一个忠实表示中,则它是单幂等的。半简单)在班级的每一个忠实代表中。因此,半单或一元性的概念是内在的。例如:
具有连续表示的紧李群
具有解析表示的复解析群
上的代数群 RR 用代数表示法。
……的一个子群 G 名为 unipotent 如果它是连通的,并且它的所有元素都是幂等的。它被称为 torus 如果它是连通的,则它是阿贝尔的,其所有元素都是半单的。这群人 G 名为 reductive 如果它没有非平凡的正规幂等子群。例如, GL(2,CC) 是还原的,但它的子群:
不是因为它有正规的幂等子群
群有一个唯一的最大正规么等子群,称为 unipotent radical ,所以它是约化的当且仅当幂等根是平凡的。
李群称为 semisimple 它是约化的,而且不存在非平凡的法环面。例如 GL(2,CC) 是还原的,但不是半简单的,因为它有一个法线环面:
这群人 SL(2,CC) 是半简单的。
基本群和中心¶
如果 G 是半单李群,则它的中心群和基本群是有限阿贝尔群。泛覆盖群 tilde G 因此是具有相同李代数的有限扩张。任何代表 G 可以被重新解释为单连接的 tilde G 。因此,我们不妨考虑 tilde G ,并将我们自己限制在简单连接的群体中。
抛物子群和Levi子群¶
让我们 G 是一个约化复数分析群。的极大可解子群 G 被称为 Borel subgroup 。所有的Borel子群都是共轭的。任何子群 P 包含Borel子群的群称为 parabolic subgroup 。我们可以写信给 P 作为其极大正规酉子群的半直积或 unipotent radical P 和一个约化子群 M ,这是由配偶关系决定的。亚群 M 被称为 Levi subgroup 。
Example: 让我们 G = GL_n(CC) 让我们 r_1, ldots, r_k 是和为 n 。然后,我们可以考虑以下形式的矩阵:
哪里 g_i in GL(r_i,CC) 。幂等根由子群组成,其中所有子群 g_i = I_{r_i} 。Levi亚群(由共轭决定)为:
and is isomorphic to M = GL(r_1,CC) times cdots times GL(r_k,CC). Therefore M is a Levi subgroup.
Levi子群的概念可以推广到紧李群。因此, U(r_1) times cdots times U(r_k) 是的Levi子群 U(n) 。然而,紧Lie群不存在抛物线子群。
Cartan型¶
半单李群是按它们的 Cartan types 。《Sage》中既有可约的Cartan类型,也有不可约的Cartan类型。让我们从不可约类型开始。这样的类型在Sage中是成对实现的 ['X', r] 其中‘X’是A、B、C、D、E、F或G中的一种 r 是正整数。如果‘X’是‘D’,那么我们一定有 r > 1 如果“X”是 exceptional types 然后是‘E’、‘F’或‘G’ r 仅限于少数几种可能性。例外类型包括:
['G', 2], ['F', 4], ['E', 6], ['E', 7] or ['E', 8].
单连通半单群是单李群的直积,单李群如下表所示。该整数 r 被称为 rank ,是最大环面的维度。
以下是与经典类型对应的李群:
紧群 |
复分析群 |
卡坦型 |
|---|---|---|
SU(r+1) |
SL(r+1,CC) |
A_r |
spin(2r+1) |
spin(2r+1,CC) |
B_r |
Sp(2r) |
Sp(2r,CC) |
C_r |
spin(2r) |
spin(2r,CC) |
D_r |
您可以按如下方式创建这些Cartan类型及其动态关系图:
sage: ct = CartanType("D5"); ct
['D', 5]
这里 "D5" 是的缩写, ['D',5] 。这群人 spin(n) 是正交群的单连通二重覆盖 SO(n) 。
双Cartan型¶
每个Cartan类型都有一个DUAL,您可以从Sage::
sage: CartanType("B4").dual()
['C', 4]
类型不是 B_r 和 C_r 为 r > 2 是自对偶的,即对偶与原始类型同构;然而,Cartan型与其对偶的同构可能会重新标记顶点。我们可以看到以下几点:
sage: CartanType("F4").dynkin_diagram()
O---O=>=O---O
1 2 3 4
F4
sage: CartanType("F4").dual()
['F', 4] relabelled by {1: 4, 2: 3, 3: 2, 4: 1}
sage: CartanType("F4").dual().dynkin_diagram()
O---O=>=O---O
4 3 2 1
F4 relabelled by {1: 4, 2: 3, 3: 2, 4: 1}
可约Cartan型¶
如果 G 是中的有限指数李群 G_1 times G_2 ,在哪里 G_1 和 G_2 是正维的李群,那么 G 名为 reducible 。在这种情况下, G 是植物根系的不相交的结合 G_1 和 G_2 ,它们位于的权空间的环境空间的正交子空间中 G 。Cartan类型的 G 是这样的 reducible 。
Sage中支持的可还原Cartan类型如下:
sage: RootSystem("A1xA1")
Root system of type A1xA1
sage: WeylCharacterRing("A1xA1")
The Weyl Character Ring of Type A1xA1 with Integer Ring coefficients
低维Cartan型¶
有一些同构在低程度上发生。
卡尔坦型 |
集团化 |
等价类型 |
同构群 |
|---|---|---|---|
B_2 |
spin(5) |
C_2 |
Sp(4) |
D_3 |
spin(6) |
A_3 |
SL(4) |
D_2 |
spin(4) |
A1 times A_1 |
SL(2)times SL(2) |
B_1 |
spin(3) |
A_1 |
SL(2) |
C_1 |
Sp(2) |
A_1 |
SL(2) |
有时,冗余的Cartan类型,如 D_3 和 D_2 被排除在Cartan类型列表之外。然而,Sage允许它们,因为排除它们会导致算法中必须做出例外。Sage遵循的一种更好的方法是允许冗余的Cartan类型,但将同构显式实现为分支规则的特殊情况。这种方法的实用性可以通过考虑排名第一的组来看出 SL(2) 有不同的自然权重格子实现,这取决于我们是否认为它是 SL(2) , spin(2) 或 Sp(2) **
sage: RootSystem("A1").ambient_space().simple_roots()
Finite family {1: (1, -1)}
sage: RootSystem("B1").ambient_space().simple_roots()
Finite family {1: (1)}
sage: RootSystem("C1").ambient_space().simple_roots()
Finite family {1: (2)}
重新标记的Cartan型¶
默认情况下,Sage使用来自 [Bourbaki46]. 由于Dykin的原因,还有另一个顶点的标记。大部分文献如下 [Bourbaki46], 尽管 [Kac] 追随着丹金。
如果您需要使用dykin的标签,您应该知道Sage确实支持重新标记的Cartan类型。请参阅中的文档 sage.combinat.root_system.type_relabel 了解更多信息。
环境空间的标准实现¶
这些实现遵循中的附录 [Bourbaki46]. 请参阅 Root system plot tutorial 如何将它们形象化。
A类¶
对于类型 A_r 我们使用一种 r+1 多维环境空间。这意味着我们正在对李群进行建模 U(r+1) 或 GL(r+1,CC) 而不是 SU(r+1) 或 SL(r+1,CC) 。环境空间被标识为 mathbf{Q}^{r+1} **
sage: RootSystem("A3").ambient_space().simple_roots()
Finite family {1: (1, -1, 0, 0), 2: (0, 1, -1, 0), 3: (0, 0, 1, -1)}
sage: RootSystem("A3").ambient_space().fundamental_weights()
Finite family {1: (1, 0, 0, 0), 2: (1, 1, 0, 0), 3: (1, 1, 1, 0)}
sage: RootSystem("A3").ambient_space().rho()
(3, 2, 1, 0)
The dominant weights consist of integer r+1-tuples lambda = (lambda_1,dots,lambda_{r+1}) such that lambda_1 ge dots ge lambda_{r+1}.
看见 SL与GL 有关A类的进一步评论,请访问。
B型¶
对于剩余的经典Cartan类型 B_r , C_r 和 D_r 我们使用一种 r -多维环境空间::
sage: RootSystem("B3").ambient_space().simple_roots()
Finite family {1: (1, -1, 0), 2: (0, 1, -1), 3: (0, 0, 1)}
sage: RootSystem("B3").ambient_space().fundamental_weights()
Finite family {1: (1, 0, 0), 2: (1, 1, 0), 3: (1/2, 1/2, 1/2)}
sage: RootSystem("B3").ambient_space().rho()
(5/2, 3/2, 1/2)
这是卡尔坦类型的 spin(2r+1) 。最后一个基本权重 (1/2, 1/2, ..., 1/2) 是最高权重的 2^r 维数 spin representation 。所有其他基本表示通过同态来表示因子 spin(2r+1) to SO(2r+1) 和是正交群的表示。
The dominant weights consist of r-tuples of integers or half-integers (lambda_1,dots,lambda_r) such that lambda_1 ge lambda_2 dots ge lambda_r ge 0, and such that the differences lambda_i - lambda_j in mathbf{Z}.
C型¶
sage: RootSystem("C3").ambient_space().simple_roots()
Finite family {1: (1, -1, 0), 2: (0, 1, -1), 3: (0, 0, 2)}
sage: RootSystem("C3").ambient_space().fundamental_weights()
Finite family {1: (1, 0, 0), 2: (1, 1, 0), 3: (1, 1, 1)}
sage: RootSystem("C3").ambient_space().rho()
(3, 2, 1)
这是辛群的Cartan型 Sp(2r) 。
The dominant weights consist of r-tuples of integers lambda = (lambda_1,dots,lambda_{r+1}) such that lambda_1 ge cdots ge lambda_r ge 0.
D型¶
sage: RootSystem("D4").ambient_space().simple_roots()
Finite family {1: (1, -1, 0, 0), 2: (0, 1, -1, 0), 3: (0, 0, 1, -1), 4: (0, 0, 1, 1)}
sage: RootSystem("D4").ambient_space().fundamental_weights()
Finite family {1: (1, 0, 0, 0), 2: (1, 1, 0, 0), 3: (1/2, 1/2, 1/2, -1/2), 4: (1/2, 1/2, 1/2, 1/2)}
sage: RootSystem("D4").ambient_space().rho()
(3, 2, 1, 0)
这是卡尔坦类型的 spin(2r) 。最后两个基本权重是两个权重中最高的一个 2^{r-1} -维自旋表示。
The dominant weights consist of r-tuples of integers lambda = (lambda_1,dots,lambda_{r+1}) such that lambda_1 ge cdots ge lambda_{r-1} ge |lambda_r|.
特殊类型¶
我们让读者来研究一下特殊的类型。您可以使用Sage列出基本的支配权重和简单根。
权重和环境空间¶
Let G be a reductive complex analytic group. Let T be a maximal torus, Lambda = X^{ast} (T) be its group of analytic characters. Then T cong (CC^{times})^r for some r and Lambda cong ZZ^r.
Example 1: Let G = hbox{GL}_{r+1} (CC). Then T is the diagonal subgroup and X^{ast} (T) cong ZZ^{r+1}. If lambda = (lambda_1, dots, lambda_n) then lambda is identified with the rational character
Example 2: Let G = hbox{SL}_{r+1} (CC). Again T is the diagonal subgroup but now if lambda in ZZ^{Delta} = {(d, cdots, d) | d in ZZ} subseteq ZZ^{r+1} then prod t_i^{lambda_i} = det ({bf t})^d = 1, so X^{ast} (T) cong ZZ^{r+1} /ZZ^{Delta} cong ZZ^r.
元素: Lambda 被称为 weights 。
If pi: G to GL(V) is any representation we may restrict pi to T. Then the characters of T that occur in this restriction are called the weights of pi.
G 通过共轭作用于其李代数( adjoint representation )。
伴随表示的非零权重称为 roots 。
The ambient space of Lambda is QQ otimes Lambda.
根系¶
As we have mentioned, G acts on its complexified Lie algebra mathfrak{g}_{CC} by the adjoint representation. The zero weight space mathfrak{g}_{CC}(0) is just the Lie algebra of T itself. The other nonzero weights each appear with multiplicity one and form an interesting configuration of vectors called the root system Phi.
It is convenient to partition Phi into two sets Phi^+ and Phi^- such that Phi^+ consists of all roots lying on one side of a hyperplane. Often we arrange things so that G is embedded in GL(n,CC) in such a way that the positive weights correspond to upper triangular matrices. Thus if alpha is a positive root, its weight space mathfrak{g}_{CC}(alpha) is spanned by a vector X_alpha, and the exponential of this eigenspace in G is a one-parameter subgroup of unipotent matrices. It is always possible to arrange that this one-parameter subgroup consists of upper triangular matrices.
If alpha is a positive root that cannot be decomposed as a sum of other positive roots, then alpha is called a simple root. If G is semisimple of rank r, then r is the number of positive roots. Let alpha_1, ldots, alpha_r be these.
Weyl群¶
Let G be a complex analytic group. Let T be a maximal torus, and let N(T) be its normalizer. Let W = N(T)/T be the Weyl group. It acts on T by conjugation; therefore it acts on the weight lattice Lambda and its ambient space. The ambient space admits an inner product that is invariant under this action. Let (v | w) denote this inner product. If alpha is a root let r_alpha denote the reflection in the hyperplane of the ambient space that is perpendicular to alpha. If alpha = alpha_i is a simple root, then we use the notation s_i to denote r_alpha.
然后 s_1, ldots, s_r 生成 W ,这是一种 Coxeter group 。这意味着它是由元素生成的 s_i 二阶的,如果 m(i,j) 的顺序是 s_i s_j ,那么
is a presentation. An important function ell : W to ZZ is the length function, where ell(w) is the length of the shortest decomposition of w into a product of simple reflections.
双重根系¶
这个 coroots 是环境空间上的某些线性泛函,它们也构成了一个根系。由于环境空间允许 W -不变内积 (|) ,它们可以被识别为环境空间本身的元素。然后它们与根成比例,尽管如果根的长度不同,长根对应短根,反之亦然。与根相对应的根 alpha 是
我们也可以用这个不变的内积来描述根和根之间的自然配对
动态金图¶
动态图是一个图,它的顶点与集合的单根是双射的。我们连接与非正交的根相对应的顶点。通常两个这样的根(顶点)成一个角 2pi/3 ,在这种情况下,我们用一个键将它们联系起来。偶尔,他们可能会从一个角度 3pi/4 在这种情况下,我们用双键将它们连接起来,或者 5pi/6 在这种情况下,我们用三重键将它们连接起来。如果键是单键,则根部相对于周围空间上的内积具有相同的长度。在双键或三键的情况下,问题中的两个简单根的长度不同,键被画成从长根到短根的箭头。仅限特殊群体 G_2 有三重键。
有多种方法可以在Sage::中获取动态金图:
sage: DynkinDiagram("D5")
O 5
|
|
O---O---O---O
1 2 3 4
D5
sage: ct = CartanType("E6"); ct
['E', 6]
sage: ct.dynkin_diagram()
O 2
|
|
O---O---O---O---O
1 3 4 5 6
E6
sage: B4 = WeylCharacterRing("B4"); B4
The Weyl Character Ring of Type B4 with Integer Ring coefficients
sage: B4.dynkin_diagram()
O---O---O=>=O
1 2 3 4
B4
sage: RootSystem("G2").dynkin_diagram()
3
O=<=O
1 2
G2
Cartan矩阵¶
Consider the natural pairing langle,rangle between coroots and roots, then the defining matrix of this pairing is called the Cartan matrix. That is to say, the Cartan matrix A = (a_{ij})_{ij} is given by
这唯一地对应于根系统/动态金图/李群。
我们注意到,我们已经做出了约定选择,而相反的约定对应于接受Cartan矩阵的转置。
基本权与Weyl向量¶
有一定的权重 omega_1, ldots, omega_r 那就是:
如果 G 是半简单的,则它们是唯一确定的,而如果 G 是还原的,但不是半简单的,我们可以方便地选择它们。
让我们 rho 是基本支配权重之和。如果 G 是半简单的,那么 rho 是正根之和的一半。万一 G 不是半简单的,我们已经注意到,基本权不完全由上面给出的内积条件决定。如果我们做出不同的选择,那么 rho 被与所有根垂直的向量改变。对于许多目的来说,这是一个无害的改变,比如Weyl字符公式。
在Sage中,这个问题只出现在Cartan类型 A_r 。看见 SL与GL 。
表象和人物¶
Let T be a maximal torus and Lambda = X^{ast} (T) be the group of rational characters. Then Lambda cong ZZ^r.
回想一下, Lambda cong ZZ^r 被称为 weights 。
Weyl群 W = N(T)/T 作用于 T ,因此 Lambda 及其周围空间的共轭。
The ambient space QQ otimes X^{ast} (T) cong QQ^r has a fundamental domain mathcal{C}^+ for the Weyl group W called the positive Weyl chamber. Weights in mathcal{C}^+ are called dominant.
Then mathcal{C}^+ consists of all vectors such that (alpha | v) geq 0 for all positive roots alpha.
它很有用,可以嵌入 Lambda 在……里面 RR^r 并将权重视为格点。
If (pi, V) is a representation then restricting to T, the module V decomposes into a direct sum of weight eigenspaces V(mu) with multiplicity m (mu) for weight mu.
There is a unique highest weight lambda with respect to the partial order. We have lambda in mathcal{C} and m (lambda) = 1.
V longleftrightarrow lambda gives a bijection between irreducible representations and weights lambda in mathcal{C}^+.
Assuming that G is simply-connected (or more generally, reductive with a simply-connected derived group) every dominant weight lambda is the highest weight of a unique irreducible representation pi_lambda, and lambda mapsto pi_lambda gives a parametrization of the isomorphism classes of irreducible representations of G by the dominant weights.
The character of pi_lambda is the function chi_lambda(g) = tr(pi_lambda(g)). It is determined by its values on T. If mathbf(z) in T and mu in Lambda, let us write mathbf{z}^mu for the value of mu on mathbf{z}. Then the character:
有时这是这样写的
的含义 e^lambda 是可以解释的,但我们可以把它看作是加法群的形象 Lambda 在它的群代数中。然后,该特征标被认为是这个环的一个元素,即 Lambda 。
表示法:示例¶
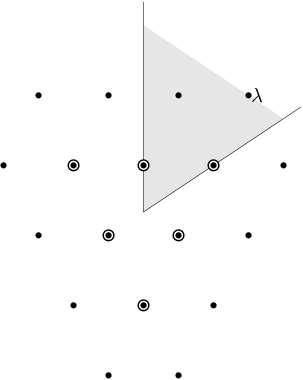
In this example, G = hbox{SL}(3,CC). We have drawn the weights of an irreducible representation with highest weight lambda. The shaded region is mathcal{C}^+. lambda is a dominant weight, and the labeled vertices are the weights with positive multiplicity in V(lambda). The weights weights on the outside have m(mu) = 1, while the six interior weights (with double circles) have m(mu) = 2.
分拆与Schur多项式¶
这一部分的考虑是针对以下类型的 A 。我们回顾了人物之间的关系 GL(n,CC) 和对称函数理论。
A partition lambda 是一系列递减的非负整数:
We do not distinguish between two partitions if they differ only by some trailing zeros, so (3, 2) = (3, 2, 0). If l is the last integer such that lambda_l > 0 then we say that l is the length of lambda. If k = sum lambda_i then we say that lambda is a partition of k and write lambda vdash k.
A partition of length le n=r+1 is therefore a dominant weight of
type ['A',r]. Not every dominant weight is a partition, since the
coefficients in a dominant weight could be negative. Let us say that
an element mu = (mu_1, mu_2, cdots, mu_n) of the ['A',r]
root lattice is effective if the mu_i ge 0. Thus an effective
dominant weight of ['A',r] is a partition of length le n, where
n = r+1.
Let lambda be a dominant weight, and let chi_lambda be the character of GL(n,CC) with highest weight lambda. If k is any integer we may consider the weight mu = (lambda_1+k,dots,lambda_n+k) obtained by adding k to each entry. Then chi_{mu} = det^k otimes chi_lambda. Clearly by choosing k large enough, we may make mu effective.
So the characters of irreducible representations of GL(n,CC) do not all correspond to partitions, but the characters indexed by partitions (effective dominant weights) are enough that we can write any character det^{-k}chi_{mu} where mu is a partition. If we take k = -lambda_n we could also arrange that the last entry in lambda is zero.
If lambda is an effective dominant weight, then every weight that appears in chi_lambda is effective. (Indeed, it lies in the convex hull of w(lambda) where w runs through the Weyl group W = S_n.) This means that if
then chi_lambda(g) is a polynomial in the eigenvalues of g. This is the Schur polynomial s_lambda(z_1, ldots, z_n).
仿射Cartan型¶
也有仿射Cartan型,它对应于(无限维)仿射李代数。有仿射Cartan类型的形式 [`X`, r, 1] 如果 X=A,B,C,D,E,F,G 和 [`X`, r] 是一种普通的卡坦型。也有 twisted affine types 表格中的 [X, r, k] ,在哪里 k = 2 或 3 如果普通Cartan型的动态图 [X, r] 有一个度的自同构 k 。什么时候 k = 1 ,仿射Cartan型据说是 untwisted 。
举例说明了可用于无扭仿射Cartan型的一些方法 ['A', 4, 1] **
sage: ct = CartanType(['A',4,1]); ct
['A', 4, 1]
sage: ct.dual()
['A', 4, 1]
sage: ct.classical()
['A', 4]
sage: ct.dynkin_diagram()
0
O-----------+
| |
| |
O---O---O---O
1 2 3 4
A4~
扭曲仿射Cartan类型是某些非扭曲Cartan类型的对偶的重新标记::
sage: CartanType(['A',3,2])
['B', 2, 1]^*
sage: CartanType(['D',4,3])
['G', 2, 1]^* relabelled by {0: 0, 1: 2, 2: 1}
仿射根与扩展的动态图¶
对于扩展的动态图,我们增加了一个负根 alpha_0 。对于非扭曲类型,这是其负数在伴随表示中的最高权重的根。有时这被称为 affine root 。我们像以前一样,通过测量根部之间的夹角来制作动态金图。这个扩展的动态图用于许多目的,例如寻找极大子群和描述仿射Weyl群。
特别是,用于反射的超平面 r_0 ,用于生成仿射Weyl群,从原点平移(因此它成为仿射超平面)。现在,根系统不被描述为欧几里得空间上的线性变换,而是由 affine 变形。因此,占主导地位的腔室具有有限的体积,并铺满了欧几里德空间。此外,每个这样的瓦片对应于仿射Weyl群中的唯一元素。
扩展的动态金图可以作为对应的无扭仿射类型的动态金图获得:
sage: ct = CartanType("E6"); ct
['E', 6]
sage: ct.affine()
['E', 6, 1]
sage: ct.affine() == CartanType(['E',6,1])
True
sage: ct.affine().dynkin_diagram()
O 0
|
|
O 2
|
|
O---O---O---O---O
1 3 4 5 6
E6~
扩展的动态图也是一种方法 WeylCharacterRing **
sage: WeylCharacterRing("E7").extended_dynkin_diagram()
O 2
|
|
O---O---O---O---O---O---O
0 1 3 4 5 6 7
E7~
我们注意到以下与经典案例的重要区别:
仿射Weyl群都是无限的。
类型 A_1^{(1)} 有两个反平行的根部,具有明显的反射。在这种情况下,动态金图由一个带有双向箭头的双键表示。
扭曲仿射根系¶
用于建造 alpha_0 在扭曲类型中,我们请读者参阅第8章 [Kac]. 如上所述,大多数扭曲类型可以通过取非扭曲类型的双重根系来构建。然而,该类型 A_{2n}^{(2)} 只能通过中定义的扭转过程构建根系 [Kac]. 它具有以下属性:
活字的动态图解 A_2^{(2)} 有一个从短根指向长根的箭头的四重键。
类型 A_{2n}^{(2)} 为 n > 1 有3个不同的根长。
进一步的概括¶
If a root system (on an Euclidean space) has only the angles pi/2, 2pi/3, 3pi/4, 5pi/6 between its roots, then we call the root system crystallographic (on :wikipedia:`Root_system`, this condition is called integrality since for any two roots we have langle beta, alpha rangle in ZZ). So if we look at the reflection group generated by the roots (this is not a Weyl group), we get general :wikipedia:`Coxeter groups <Coxeter_group>` (with non-infinite labels) and non-crystallographic Coxeter groups are not connected with Lie theory.
然而,我们可以推广动态金图(等价于Cartan矩阵),使其所有边都标记为 (a, b) 哪里 a, b in ZZ_{>0} 并对应于拥有 a 箭头指向一个方向 b 指向对方的箭头。例如,在类型中 A_{1}^{(1)} ,我们有一个优势 (2, 2) ,或在文字上 A_{2}^{(2)} ,我们有一个优势 (1, 4) (相当于 (4, 1) )。这些边标签位于 i 和 j 对应于条目 a_{ij} 和 a_{ji} 在卡尔坦矩阵中。它们被用来构造一类(通常是无限维的)李代数,称为Kac-Moody(Lie)代数,而Kac-Moody(Lie)代数又被用来构造量子群。我们请读者参阅 [Kac] 和 [HongKang2002] 以获取更多信息。