摘要: 既有方向又有大小的量叫做向量（物理学中叫做矢量），向量可以用小写黑体字母a，b，c，.......表达，也可以用表示向量的有向线段的起点和结尾字母表明。仅有大小没有方向的量叫做数量。在自然界中，有很多量既有大小又有方向，如力、速度等。我们为了研讨这些量的这个共...
既有方向又有大小的量叫做向量（物理学中叫做矢量），向量可以用小写黑体字母a，b，c，.......表达，也可以用表示向量的有向线段的起点和结尾字母表明。仅有大小没有方向的量叫做数量。在自然界中，有很多量既有大小又有方向，如力、速度等。我们为了研讨这些量的这个共性，在它们的基础上提取出了向量这个概念。这样，研究明白了向量的性质，当然用它来研讨其它量，就会方便很多。
向量(矢量)这个术语作为现代数学-物理学中的一个主要概念，首先是由英国数学家哈密顿使用的。向量的名词虽来自哈密顿，但向量作为一条有向线段的思路却由来已久。向量理论的来源与开展主要有三条头绪：物理学中的速度和力的平行四边形法则、位置几何、复数的几何表示。
物理学中的速度与力的平行四边形概念是向量理论的一个主要起源之一。18世纪中期之后，欧拉、拉格朗日、拉普拉斯和柯西等的工作，直接导致了在19世纪中期向量力学的成立。与此同时，向量概念是近代数学中主要和基本的概念之一，有着深刻的几何背景。它始于莱布尼兹的位置几何。
如今向量理论是在复数的几何表示这条头绪上发展起来的。18世纪，因为在一些数学的推导中用到复数，复数的几何表示变成人们讨论的热门。哈密顿在做3维复数的模仿物的过程中发现了四元数。随后，吉布斯和亥维赛在四元数基础上发明了向量分析系统，最终被广为接受。那向量我们应该怎么表示呢？如下：
1、几何表示
具有方向的线段叫做有向线段，我们以A为起点、B为结尾的有向线段记作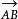
，则向量能够相应地记作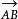。可是，区别于有向线段，在通常的数学研究中，向量是能够平移的。
2、坐标表示
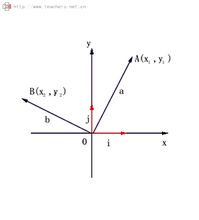
在直角坐标系内，我们各取与x轴、y轴方向一样的两个单位向量i、j作为基底。任作一个向量a，由平面向量基本定理可知，有且仅有一对实数x、y，使得：a=xi+yj，我们把(x,y)叫做向量a的坐标，记作：a=(x,y)。
其中x叫做a在x轴上的坐标，y叫做a在y轴上的坐标，上式叫做向量的坐标表示。在平面直角坐标系内，每一个平面向量都能够用一对实数表示。
依据定义，任取平面上两点A(x1,y1)，B(x2,y2)，则向量AB=(x2-x1,y2-y1)，即一个向量的坐标等于表示此向量的有向线段的终点坐标减去始点的坐标。
向量和数量一样，也可以进行计算。向量可以进行多种运算过程，包括线性运算、数量积、向量积与混合积等。
