等面积投影图的优点和示例

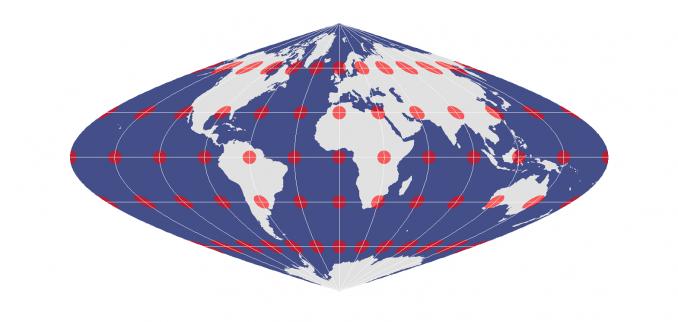
等面积投影图的优点和示例

等面积投影会在整个地图上保留该区域的相对大小。 因此，这意味着在地图中的任何给定区域，均等面积的投影将保留要素的真实大小。 尽管等面积投影保留了面积，但它扭曲了形状、角度且不能保形。 让我们回顾一下使用等面积投影图的优势和示例。

等面积投影图的示例

如下例所示，等面积投影图保留了真实面积的要素大小。 例如，密切关注格陵兰岛如何在每张地图上保留其真实的区域大小。

1.Behrmann

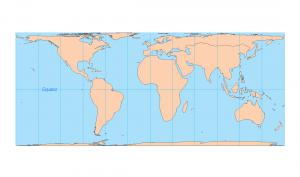
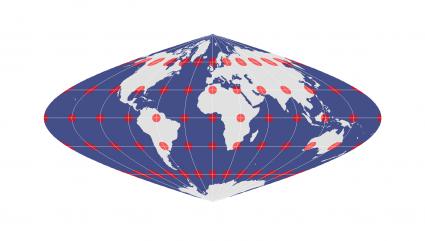
2.Sinusoidal

3.Mollweide

4.Hammer Aitoff

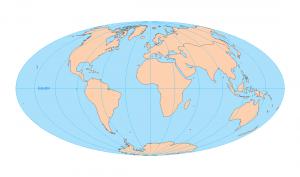
5.Bonne

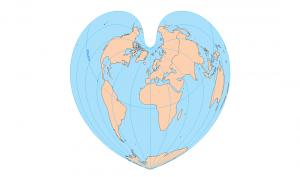
但是，如果查看下面的墨卡托投影图， 格陵兰岛由于两极区域的扭曲而变得异常大。

且南极洲看起来比所有其他大洲都要大。

USGS使用Albers等面积圆锥投影

USGS通常使用Albers等面积圆锥曲线投影， 显示了如何按比例表示同一地区的美国。

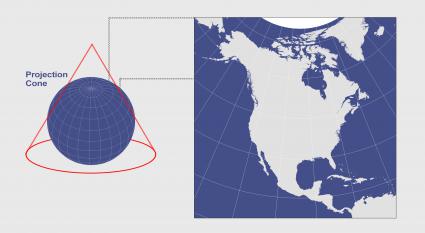
H. C. Albers于1805年首次引入了带有两个标准平行线（割线）的地图投影。 从那时起，制图师就使用它来显示需要等面积表示的大国。

像所有地图投影一样， “Albers等面积圆锥投影”也会扭曲地图中的其他属性。 例如，距离和比例尺仅在两个标准平行线上都适用。

尽管方向是相当准确的，但它不是共形的，透视的或等距的。

天梭圆与变形

在等面积投影中，天梭圆在地图上的相对大小都相同。

尽管天梭指标显示了如何从一个圆形变为一个椭圆形， 但相等区域投影仍保留相对大小。

所以，现在您知道相等区域投影的工作原理， 我们有一个部分完全致力于地图中发现的失真类型。

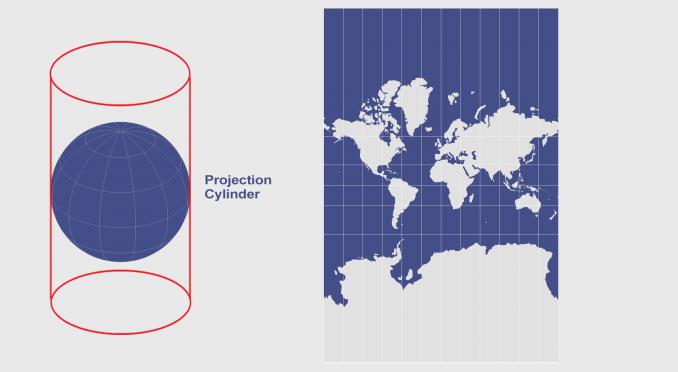
另外，我们还介绍了圆锥，圆柱体 和平面等可展开表面， 以及它们如何将3D地球扁平化为二维地图。

您最喜欢的等面积投影类型有哪些？请在下面发表评论让我们知道。