样本均值和样本方差
访问量: 167 次浏览
样本均值
样本均值又叫样本均数。即为样本的均值。均值是指在一组数据中所有数据之和再除以数据的个数。 它是反映数据集中趋势的一项指标。例如 1、2、3、4 四个数据的均值为(1+2+3+4)/4=2.5。
样本,是指从总体中抽出的一部分个体。 样本中所包含个体数目称样本容量或含量用符号N或n表示。
总体是指客观存在的,并在统一性质的基础上结合起来的许多个别单位的整体, 即具有某一特性的一类事物的全体,又叫母体或全域。简单地说,总体也就是我们所研究的性质相同个体的总和。
样本是受审查客体的反映形象或其自身的一部分。按一定方式从总体中抽取的若干个体, 用于提供总体的信息及由此对总体作统计推断。又称子样。例如因为人力和物力所限, 不能每年对全国的人口进行普查,但可以通过抽样调查的方式来得到需要的信息。 从总体中抽取样本的过程叫抽样。最常用的抽样方式是简单随机抽样, 按这种方式抽样,总体中每个个体都有同等的机会被抽入样本, 这样得到的样本称简单随机样本。样本的平均值称样本均值, 样本偏离样本均值的平方的平均值称为样本方差,在数理统计中, 常常用样本均值来估计总体均值,用样本方差来估计总体方差。
样本方差
样本方差为构成样本的随机变量对离散中心x之离差的平方和除以n-1用来表示一列数的变异程度。
样本关于给定点x在直线上散布的数字特征之 一,其中的点x称为方差中心。 样本方差数值上等于构成样本的随机变量对离散中心 x之方差的平方和。 设X、,…,各是同分布实随机变 量,点x是选定的方差中心(x〔R’)。 那么,量 s。\((x)=E(x一x)z\) 称为关于点x的样本方差。
实际上,样本方差可以理解成是对所给样本的方差做出的一个无偏估计。
方差定义
设x是一个随机变量,若E{[X-E(X)]2}存在, 则称E{[X-E(X)]2}为X的方差,记为V(X),是衡量一组数据的离散程度的统计量。
计算方法
样本方差
假设x1,x2,…,xn是一个样本,则样本方差的计算公式为:
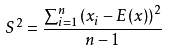
其中E(x)是样本均值。
例如,一样本取值为3,4,4,5,4,
则样本均值=\( \frac {3+4+4+5+4}{5} =4\)
样本方差\(S^2= \frac {(3-4)^2+(4-4)^2+(4-4)^2+(5-4)^2+(4-4)^2}{5-1} =0.5\)
样本方差是常用的统计量之一,是描述一组数据变异程度或分散程度大小的指标。
样本标准差
S称为样本标准差。如在上例中,\(S=0.7071\)。称(S/ X) ×100%为样本变异系数。 由于S与X都是从同一个样本资料中求得,两者的单位相同,故变异系数为一纯数。 当两种样本资料所用的单位不同时,只要计算出变异系数,就可以比较它们的变异程度。
本文链接 :样本均值和样本方差