6.1. 傅里叶变换¶
6.1.1. 目标¶
6.1.2. 理论¶
利用傅里叶变换分析了各种滤波器的频率特性。对于图像, 二维离散傅里叶变换(DFT) 用于查找频域。一种叫做 快速傅里叶变换 用于计算DFT。这些细节可以在任何图像处理或信号处理教科书中找到。请看 Additional Resources 部分。
对于正弦信号, \(x(t) = A \sin(2 \pi ft)\) ,我们可以说 \(f\) 是信号的频率,如果取它的频域,我们可以看到 \(f\) . 如果对信号进行采样形成离散信号,我们得到相同的频域,但在该范围内是周期性的 \([- \pi, \pi]\) 或 \([0,2\pi]\) (或) \([0,N]\) 对于N点DFT)。您可以将图像视为在两个方向上采样的信号。所以在X和Y方向上进行傅里叶变换可以得到图像的频率表示。
更直观地说,对于正弦信号,如果振幅在短时间内变化如此之快,可以说是高频信号。如果变化缓慢,那就是低频信号。你可以把同样的想法延伸到图像上。图像中的振幅在哪里剧烈变化?在边缘点,或噪音。所以我们可以说,边缘和噪声是图像中的高频成分。如果振幅没有太大变化,那就是低频分量。(一些链接被添加到 Additional Resources 用实例直观地解释了频率变换。
现在我们来看看如何找到傅里叶变换。
6.1.3. 傅里叶变换¶
首先我们将看到如何使用Numpy找到傅里叶变换。Numpy有一个FFT包来完成这个任务。 np.fft.fft2() 为我们提供一个复杂阵列的频率变换。它的第一个参数是输入图像,它是灰度的。第二个参数是可选的,它决定输出数组的大小。如果大于输入图像的大小,则在计算FFT之前用零填充输入图像。如果小于输入图像,则将剪切输入图像。如果未传递参数,则输出数组大小将与输入相同。
现在得到结果后,零频率分量(DC分量)将位于左上角。如果你想把它带到中心,你需要通过 \(\frac{{N}}{{2}}\) 在两个方向上。这只是由函数来完成的, np.fft.fftshift() . (更容易分析)。找到频率变换后,就可以找到幅度谱。
>>> %matplotlib inline
>>> import cv2
>>> import numpy as np
>>> from matplotlib import pyplot as plt
>>>
>>> img = cv2.imread('/cvdata/messi5.jpg',0)
>>> f = np.fft.fft2(img)
>>> fshift = np.fft.fftshift(f)
>>> magnitude_spectrum = 20*np.log(np.abs(fshift))
>>>
>>> plt.subplot(121),plt.imshow(img, cmap = 'gray')
>>> plt.title('Input Image'), plt.xticks([]), plt.yticks([])
>>> plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
>>> plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
>>> plt.show()

结果如下:
看,你可以在中心看到更白的区域,显示低频内容更多。
所以你找到了频率变换,现在你可以在频域做一些操作,比如高通滤波和重建图像,即找到逆DFT。为此,您只需通过使用大小为60x60的矩形窗口进行掩蔽来消除低频。然后使用 np.fft.ifftshift() 所以直流分量又出现在左上角。然后使用 np.ifft2() 功能。结果同样是一个复数。你可以取它的绝对值。
>>> rows, cols = img.shape
>>> crow,ccol = int(rows/2) , int(cols/2)
>>> crow
171
>>> ccol
274
>>> fshift
array([[ -124. +0.j , -42.19440414 -877.03617166j,
223.27548059+1046.60850634j, ...,
1202.61938833 +206.61865249j, 223.27548059-1046.60850634j,
-42.19440414 +877.03617166j],
[ 208.74536514 +64.60669315j, 1002.28500993 -234.50419799j,
1506.32632304+1222.65769814j, ...,
-1389.57648774 -150.87464627j, 109.36759417 +488.69796424j,
-57.03604421 +606.24574085j],
[ 900.36223857 +317.76577457j, 653.10253934 -411.72777201j,
-1280.58956522+1186.46570157j, ...,
-121.90161098+1372.27974992j, 519.73405635 +156.14284965j,
-549.90306456 -294.50881028j],
...,
[ 222.83408186 -992.83030536j, 12.48466653+1024.31486962j,
627.72474919 -709.13462585j, ...,
1305.90353042 +971.79340223j, -1576.22476438-1240.03645033j,
768.60806672+1088.72533153j],
[ 900.36223857 -317.76577457j, -549.90306456 +294.50881028j,
519.73405635 -156.14284965j, ...,
461.36292583+1732.90045983j, -1280.58956522-1186.46570157j,
653.10253934 +411.72777201j],
[ 208.74536514 -64.60669315j, -57.03604421 -606.24574085j,
109.36759417 -488.69796424j, ...,
-1478.63347024+1111.98404021j, 1506.32632304-1222.65769814j,
1002.28500993 +234.50419799j]])
>>> fshift[crow-30:crow+30, ccol-30:ccol+30] = 0
>>> f_ishift = np.fft.ifftshift(fshift)
>>> img_back = np.fft.ifft2(f_ishift)
>>> img_back = np.abs(img_back)
>>>
>>> plt.subplot(131),plt.imshow(img, cmap = 'gray')
>>> plt.title('Input Image'), plt.xticks([]), plt.yticks([])
>>> plt.subplot(132),plt.imshow(img_back, cmap = 'gray')
>>> plt.title('Image after HPF'), plt.xticks([]), plt.yticks([])
>>> plt.subplot(133),plt.imshow(img_back)
>>> plt.title('Result in JET'), plt.xticks([]), plt.yticks([])
>>>
>>> plt.show()

结果如下:
结果表明,高通滤波是一种边缘检测操作。这是我们在图像渐变章节中看到的。这也表明大部分图像数据存在于频谱的低频区域。不管怎样,我们已经看到了如何在纽比找到DFT,IDFT等。现在让我们看看如何在OpenCV中实现它。
如果你仔细观察结果,特别是最后一张喷射颜色的图像,你可以看到一些伪影(我用红色箭头标记的一个实例)。它显示了一些波纹状的结构,它被称为 振铃效应 . 这是由我们用来遮罩的矩形窗户造成的。此掩码转换为导致此问题的sinc形状。所以矩形窗口不用于过滤。更好的选择是高斯窗口。
6.1.4. OpenCV中的傅里叶变换¶
OpenCV提供了 cv2.dft() 和 cv2.idft() 为了这个。它返回与前面相同的结果,但有两个通道。第一个通道将具有结果的实部,第二个通道将具有结果的虚部。输入图像应首先转换为np.float32。我们看看怎么做。
>>> import numpy as np
>>> import cv2
>>> from matplotlib import pyplot as plt
>>>
>>> img = cv2.imread('/cvdata/messi5.jpg',0)
>>>
>>> dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
>>> dft_shift = np.fft.fftshift(dft)
>>>
>>> magnitude_spectrum = 20*np.log(cv2.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))
>>>
>>> plt.subplot(121),plt.imshow(img, cmap = 'gray')
>>> plt.title('Input Image'), plt.xticks([]), plt.yticks([])
>>> plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
>>> plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
>>> plt.show()

注意
您也可以使用 心血管2.软骨() 在一次拍摄中同时返回幅度和相位
所以,现在我们要做逆DFT。在前一个会话中,我们创建了一个HPF,这次我们将看到如何删除图像中的高频内容,即我们将LPF应用于图像。它实际上模糊了图像。为此,我们首先创建一个低频高值(1)的掩模,即我们通过低频内容,高频区域为0。
>>> rows, cols = img.shape
>>> crow,ccol = int(rows/2) , int(cols/2)
>>>
>>> # create a mask first, center square is 1, remaining all zeros
>>> mask = np.zeros((rows,cols,2),np.uint8)
>>> mask[crow-30:crow+30, ccol-30:ccol+30] = 1
>>>
>>> # apply mask and inverse DFT
>>> fshift = dft_shift*mask
>>> f_ishift = np.fft.ifftshift(fshift)
>>> img_back = cv2.idft(f_ishift)
>>> img_back = cv2.magnitude(img_back[:,:,0],img_back[:,:,1])
>>>
>>> plt.subplot(121),plt.imshow(img, cmap = 'gray')
>>> plt.title('Input Image'), plt.xticks([]), plt.yticks([])
>>> plt.subplot(122),plt.imshow(img_back, cmap = 'gray')
>>> plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
>>> plt.show()

查看结果:
注意
像往常一样,OpenCV函数 cv2.dft() 和 cv2.idft() 比核电站的同行要快。但是Numpy的功能更加友好。有关性能问题的更多详细信息,请参阅下面的部分。
6.1.5. DFT的性能优化¶
对于一定的阵列尺寸,DFT计算的性能更好。当数组大小是2的幂时,它是最快的。其大小是2、3和5的乘积的数组也被非常有效地处理。因此,如果您担心代码的性能,可以在找到DFT之前将数组的大小修改为任何最佳大小(填充零)。对于OpenCV,必须手动填充零。但是对于Numpy,您可以指定FFT计算的新大小,它会自动为您填充零。
那么我们如何找到这个最佳尺寸呢?OpenCV提供了一个函数, 获取最佳dftsize() 为了这个。适用于 cv2.dft() 和 np.fft.fft2() . 让我们使用IPython magic命令检查它们的性能 %timeit .
>>> img = cv2.imread('/cvdata/messi5.jpg',0)
>>> rows,cols = img.shape
>>> rows,cols
(342, 548)
>>> nrows = cv2.getOptimalDFTSize(rows)
>>> ncols = cv2.getOptimalDFTSize(cols)
>>> nrows, ncols
(360, 576)
请参见,大小(342548)修改为(360576)。现在让我们用零填充它(对于OpenCV)并找到它们的DFT计算性能。您可以创建一个新的大零数组并将数据复制到其中,或者使用 cv2.copyMakeBorder() .
>>> nimg = np.zeros((nrows,ncols))
>>> nimg[:rows,:cols] = img
或:
>>> right = ncols - cols
>>> bottom = nrows - rows
>>> bordertype = cv2.BORDER_CONSTANT #just to avoid line breakup in PDF file
>>> nimg = cv2.copyMakeBorder(img,0,bottom,0,right,bordertype, value = 0)
现在我们计算Numpy函数的DFT性能比较:
>>> %timeit fft1 = np.fft.fft2(img)
10 loops, best of 5: 31.4 ms per loop
>>> # 10 loops, best of 3: 40.9 ms per loop
>>>
>>> %timeit fft2 = np.fft.fft2(img,[nrows,ncols])
100 loops, best of 5: 10.1 ms per loop
>>>
>>> # 100 loops, best of 3: 10.4 ms per loop
它显示了4倍的加速。现在我们将对OpenCV函数进行同样的尝试。
>>> %timeit dft1= cv2.dft(np.float32(img),flags=cv2.DFT_COMPLEX_OUTPUT)
>>> # 100 loops, best of 3: 13.5 ms per loop
100 loops, best of 5: 11.6 ms per loop
>>>
>>> %timeit dft2= cv2.dft(np.float32(nimg),flags=cv2.DFT_COMPLEX_OUTPUT)
>>> # 100 loops, best of 3: 3.11 ms per loop
100 loops, best of 5: 2.55 ms per loop
它还显示了4倍的速度。您还可以看到OpenCV函数比Numpy函数快3倍左右。这也可以测试反FFT,这留给您作为练习。
6.1.6. 为什么拉普拉斯是高通滤波器?¶
在一个论坛上也提出了类似的问题。问题是,为什么拉普拉斯是高通滤波器?为什么索贝尔是一个高性能战斗机?等等,第一个答案是傅里叶变换。对于一些较大的FFT,只需对Laplacian进行fourier变换。分析一下:
>>> import cv2
>>> import numpy as np
>>> from matplotlib import pyplot as plt
>>>
>>> # simple averaging filter without scaling parameter
>>> mean_filter = np.ones((3,3))
>>>
>>> # creating a guassian filter
>>> x = cv2.getGaussianKernel(5,10)
>>> gaussian = x*x.T
>>>
>>> # different edge detecting filters
>>> # scharr in x-direction
>>> scharr = np.array([[-3, 0, 3],
>>> [-10,0,10],
>>> [-3, 0, 3]])
>>> # sobel in x direction
>>> sobel_x= np.array([[-1, 0, 1],
>>> [-2, 0, 2],
>>> [-1, 0, 1]])
>>> # sobel in y direction
>>> sobel_y= np.array([[-1,-2,-1],
>>> [0, 0, 0],
>>> [1, 2, 1]])
>>> # laplacian
>>> laplacian=np.array([[0, 1, 0],
>>> [1,-4, 1],
>>> [0, 1, 0]])
>>>
>>> filters = [mean_filter, gaussian, laplacian, sobel_x, sobel_y, scharr]
>>> filter_name = ['mean_filter', 'gaussian','laplacian', 'sobel_x', \
>>> 'sobel_y', 'scharr_x']
>>> fft_filters = [np.fft.fft2(x) for x in filters]
>>> fft_shift = [np.fft.fftshift(y) for y in fft_filters]
>>> mag_spectrum = [np.log(np.abs(z)+1) for z in fft_shift]
>>>
>>> for i in range(6):
>>> plt.subplot(2,3,i+1),plt.imshow(mag_spectrum[i],cmap = 'gray')
>>> plt.title(filter_name[i]), plt.xticks([]), plt.yticks([])
>>>
>>> plt.show()
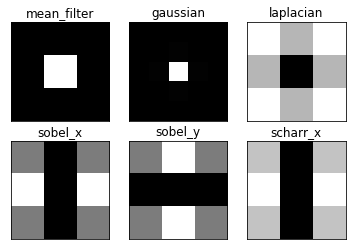
查看结果:
从图像中,您可以看到每个内核块的频率区域,以及它经过的区域。根据这些信息,我们可以解释为什么每个内核都是HPF或LPF