多样性计算 (skbio.diversity )¶
这个软件包提供了分析生物多样性的功能。它实现了alpha和beta多样性的度量,并提供了两个“驱动函数”,它们是scikit bio计算α和β多样性的主要接口。另外还提供了支持发现可用多样性度量的函数。本文档对如何使用 skbio.diversity 模块,并且应该是使用该模块之前阅读的第一个文档。
驱动程序功能¶
驾驶员的功能, skbio.diversity.alpha_diversity 和 skbio.diversity.beta_diversity ,用于计算一个或多个样本的α分集,或计算一对或多对样本的beta分集。分集驱动函数接受包含每个样本中otu频率向量的矩阵。
我们在这里使用术语“OTU”非常松散,因为这些实际上可以代表不同的特征类型,包括细菌种类、基因和代谢物。为了这些目的,“样品”一词的定义也很松散。这些都是为了代表一个单一的抽样单位,因此,一个单一的样本所代表的可能有很大的不同。例如,在微生物组调查中,这些可以代表来自一个口腔拭子的所有16srrna基因序列。另一方面,在比较基因组学研究中,一个样本可以代表一个生物体的基因组。
给定向量中的每个频率代表特定OTU观察到的个体数量。我们将单个样本的相关频率称为 计数向量 或 counts 在整个文档中。计数向量是 array_like :任何可以转换为一维numpy数组的内容都是可接受的输入。例如,您可以提供一个numpy数组或一个原生Python列表,结果将是相同的。如上所述,驱动函数在矩阵中接受这些向量中的一个或多个(代表一个或多个样本),该矩阵也是 array_like . 矩阵中的每一行表示单个样本的计数向量,因此行表示样本,列表示otu。
一些多样性度量通过参考系统发生树在计算中加入了otu之间的关系。这些指标还需要 skbio.TreeNode 对象和将计数向量中的值映射到树中的提示的OTU标识符列表。
驱动函数被优化,使得计算一次以上的分集度量(即,对于α分集度量的多个样本,或者对于beta分集度量的多对样本)通常比对度量的重复调用快得多。因此,驱动函数采用计数向量的矩阵,而不是α分集度量的单个计数向量或β分集度量的两个计数向量。这个 alpha_diversity 因此,驱动函数将计算矩阵中所有计数向量的α分集,并且 beta_diversity 驱动函数将计算矩阵中所有计数向量对的beta分集。
输入验证¶
默认情况下,驱动程序函数执行输入验证。验证可能很慢,因此可以通过传递禁用此步骤 validate=False . 然而,这可能是危险的。如果在禁用验证时遇到无效输入,则可能导致难以解释错误消息或不正确的结果。因此,我们建议用户在禁用验证之前小心确保其输入数据有效。
驱动程序功能验证的条件如下。如果禁用验证,用户应该确信这些条件满足。
计数向量中的数据可以安全地转换为整数
计数向量中没有负值
每个计数向量都是一维的
计数矩阵是二维的
所有计数向量的长度相等
此外,如果正在计算系统发育多样性度量,则还应确认以下条件:
提供的OTU标识符都是唯一的
每个计数向量的长度等于OTU标识符的数量
提供的树已生根
树有多个节点
提供的树中除根节点外的所有节点都具有分支长度
提供的树中的所有提示名称都是唯一的
所有提供的OTU标识符都对应于所提供树中的提示名称
计数向量¶
在生态学文献和相关软件中,计数向量有不同的表示方式。这里提供的多样性措施 总是 假设输入包含丰度数据:每个计数代表样本中特定OTU观察到的个体数量。例如,如果您有两个OTU,其中从第一个OTU观察到三个个体,而从第二个OTU中只观察到一个个体,那么您可以用以下形式表示这些数据(除其他外)。
作为计数向量。这是本模块中多样性度量的预期输入类型。OTU的索引0处有3个人,索引1处的OTU有1个人:
>>> counts = [3, 1]
作为指数的向量。索引0处的OTU观察3次,索引1处的OTU观察1次:
>>> indices = [0, 0, 0, 1]
作为频率向量。我们有一个OTU是单胎,1个OTU是三胎。我们没有任何0吨或双吨:
>>> frequencies = [0, 1, 0, 1]
始终将第一个表示(计数向量)用于此模块。
指定多样性度量¶
驱动程序函数需要一个参数, metric ,指定应应用哪种多样性度量。你提供的价值 metric 可以是字符串(例如。, "faith_pd" )或函数(例如。, skbio.diversity.alpha.faith_pd ). 度量通常应作为字符串传递,因为这通常使用度量的优化版本。例如,传球 metric="faith_pd" (一串)到 alpha_diversity 会比路过快几十倍 metric=skbio.diversity.alpha.faith_pd (a函数)当计算大约100个样本的Faith的PD时。同样,传球 metric="unweighted_unifrac" (一根绳子)会比传球快几百倍 metric=skbio.diversity.beta.unweighted_unifrac (一个函数)在大约100个样本上计算未加权的UniFrac时。如果只计算一个alpha或beta分集值,后者可能会更快,但在这些情况下,运行时间可能非常小,因此差异可以忽略不计。 因此,我们建议您尽可能将度量作为字符串传递。
如果您要运行的度量不是scikit bio所知道的,那么将无法将度量作为字符串传递。例如,如果您正在应用开发的自定义度量,则可能会出现这种情况。以发现scikit bio知道的作为字符串的度量名称,这些字符串可以作为 metric 到 alpha_diversity 或 beta_diversity ,你可以打电话 get_alpha_diversity_metrices 或 get_beta_diversity_metrics 分别是。这些函数返回scikit bio中实现的alpha和beta多样性度量列表。可能还有其他度量可以作为字符串传递,但不会在此处列出,例如在中实现的那些 scipy.spatial.distance.pdist .
子包¶
阿尔法多样性衡量标准(skBio.diffity.pha) |
|
贝塔多样性衡量标准(skBio.disposity.beta) |
功能¶
|
计算一个或多个样本的α多样性 |
|
计算所有样本对之间的距离 |
|
仅计算指定ID对之间的距离 |
|
执行块分解beta分集计算 |
列出scikit-bio的α多样性指标 |
|
列出scikit-bio的beta多样性指标 |
示例
创建包含6个样本(行)和7个OTU(列)的矩阵:
>>> data = [[23, 64, 14, 0, 0, 3, 1],
... [0, 3, 35, 42, 0, 12, 1],
... [0, 5, 5, 0, 40, 40, 0],
... [44, 35, 9, 0, 1, 0, 0],
... [0, 2, 8, 0, 35, 45, 1],
... [0, 0, 25, 35, 0, 19, 0]]
>>> ids = list('ABCDEF')
首先,我们将使用 alpha_diversity 驱动器功能:
>>> from skbio.diversity import alpha_diversity
>>> adiv_obs_otus = alpha_diversity('observed_otus', data, ids)
>>> adiv_obs_otus
A 5
B 5
C 4
D 4
E 5
F 3
dtype: int64
下一步我们将计算相同样本的费思的概率密度。因为这是一个系统发育多样性度量,我们首先创建一个树和一个有序的OTU标识符列表。
>>> from skbio import TreeNode
>>> from io import StringIO
>>> tree = TreeNode.read(StringIO(
... '(((((OTU1:0.5,OTU2:0.5):0.5,OTU3:1.0):1.0):0.0,'
... '(OTU4:0.75,(OTU5:0.5,(OTU6:0.5,OTU7:0.5):0.5):'
... '0.5):1.25):0.0)root;'))
>>> otu_ids = ['OTU1', 'OTU2', 'OTU3', 'OTU4', 'OTU5', 'OTU6', 'OTU7']
>>> adiv_faith_pd = alpha_diversity('faith_pd', data, ids=ids,
... otu_ids=otu_ids, tree=tree)
>>> adiv_faith_pd
A 6.75
B 7.00
C 6.25
D 5.75
E 6.75
F 5.50
dtype: float64
现在我们要计算所有样本对之间的布雷-柯蒂斯距离,一个beta分集度量。注意到 data 和 ids 参数提供给 beta_diversity 与提供给 alpha_diversity .
>>> from skbio.diversity import beta_diversity
>>> bc_dm = beta_diversity("braycurtis", data, ids)
>>> print(bc_dm)
6x6 distance matrix
IDs:
'A', 'B', 'C', 'D', 'E', 'F'
Data:
[[ 0. 0.78787879 0.86666667 0.30927835 0.85714286 0.81521739]
[ 0.78787879 0. 0.78142077 0.86813187 0.75 0.1627907 ]
[ 0.86666667 0.78142077 0. 0.87709497 0.09392265 0.71597633]
[ 0.30927835 0.86813187 0.87709497 0. 0.87777778 0.89285714]
[ 0.85714286 0.75 0.09392265 0.87777778 0. 0.68235294]
[ 0.81521739 0.1627907 0.71597633 0.89285714 0.68235294 0. ]]
接下来,我们将计算所有样本对之间的加权UniFrac距离。因为加权UniFrac是一种系统发育β多样性指标,我们需要通过 skbio.TreeNode 以及我们在上面创建的OTU ID列表。同样,这些值与提供给 alpha_diversity .
>>> wu_dm = beta_diversity("weighted_unifrac", data, ids, tree=tree,
... otu_ids=otu_ids)
>>> print(wu_dm)
6x6 distance matrix
IDs:
'A', 'B', 'C', 'D', 'E', 'F'
Data:
[[ 0. 2.77549923 3.82857143 0.42512039 3.8547619 3.10937312]
[ 2.77549923 0. 2.26433692 2.98435423 2.24270353 0.46774194]
[ 3.82857143 2.26433692 0. 3.95224719 0.16025641 1.86111111]
[ 0.42512039 2.98435423 3.95224719 0. 3.98796148 3.30870431]
[ 3.8547619 2.24270353 0.16025641 3.98796148 0. 1.82967033]
[ 3.10937312 0.46774194 1.86111111 3.30870431 1.82967033 0. ]]
接下来我们将使用这些beta分集距离矩阵做一些工作。首先,我们将通过计算UniFrac和Bray-Curtis距离矩阵之间的Mantel相关性来确定它们是否显著相关。然后我们将根据α0.05来确定p值是否有效。
>>> from skbio.stats.distance import mantel
>>> r, p_value, n = mantel(wu_dm, bc_dm)
>>> print(r)
0.922404392093
>>> alpha = 0.05
>>> print(p_value < alpha)
True
接下来,我们将对加权UniFrac距离矩阵执行主坐标分析(PCoA)。
>>> from skbio.stats.ordination import pcoa
>>> wu_pc = pcoa(wu_dm)
PCoA图只有在示例元数据的上下文中才真正有趣,所以在可视化这些结果之前,让我们先定义一些。
>>> import pandas as pd
>>> sample_md = pd.DataFrame([
... ['gut', 's1'],
... ['skin', 's1'],
... ['tongue', 's1'],
... ['gut', 's2'],
... ['tongue', 's2'],
... ['skin', 's2']],
... index=['A', 'B', 'C', 'D', 'E', 'F'],
... columns=['body_site', 'subject'])
>>> sample_md
body_site subject
A gut s1
B skin s1
C tongue s1
D gut s2
E tongue s2
F skin s2
现在,让我们绘制PCoA结果,根据样本的来源给每个样本着色:
>>> fig = wu_pc.plot(sample_md, 'subject',
... axis_labels=('PC 1', 'PC 2', 'PC 3'),
... title='Samples colored by subject', cmap='jet', s=50)
(Source code, png)
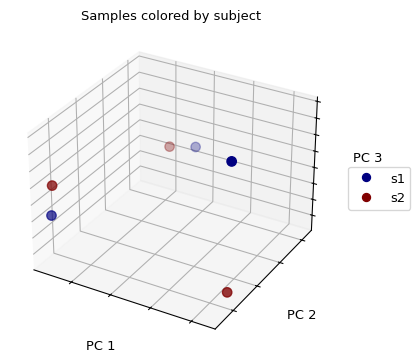
我们没有看到任何样本的聚集/分组。如果我们用从身体部位提取的样本来代替颜色,我们会发现来自同一身体部位的样本(那些颜色相同的)在三维空间中看起来更接近于另一个,然后它们与来自其他身体部位的样本相比较。
>>> import matplotlib.pyplot as plt
>>> plt.close('all') # not necessary for normal use
>>> fig = wu_pc.plot(sample_md, 'body_site',
... axis_labels=('PC 1', 'PC 2', 'PC 3'),
... title='Samples colored by body site', cmap='jet', s=50)
(Source code, png)
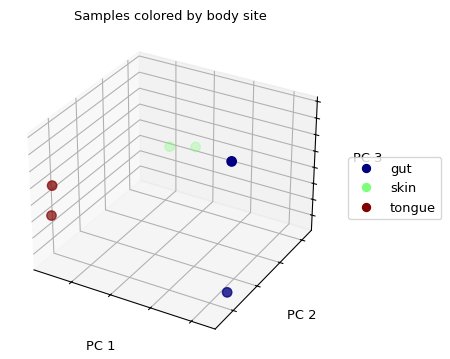
排序技术,如PCoA,对探索性分析很有用。下一步是量化我们在排序图中看到的分组/聚类的强度。有许多可用的统计方法来实现这一点;许多方法是对距离矩阵进行运算。让我们使用ANOSIM来量化我们在上面排序图中看到的聚类的强度,使用我们的加权UniFrac距离矩阵和样本元数据。
首先按受试者测试样本分组:
>>> from skbio.stats.distance import anosim
>>> results = anosim(wu_dm, sample_md, column='subject', permutations=999)
>>> results['test statistic']
-0.33333333333333331
>>> results['p-value'] < 0.1
False
ANOSIM的R统计量的负值表示反聚类,在α为0.1时p值不显著。
现在让我们测试按身体部位分组的样本:
>>> results = anosim(wu_dm, sample_md, column='body_site', permutations=999)
>>> results['test statistic']
1.0
>>> results['p-value'] < 0.1
True
R统计量表明,基于身体部位的样本具有很强的分离性。p值在α为0.1时显著。
我们还可以在示例元数据的上下文中探索alpha多样性。为此,让我们将观察到的OTU和Faith PD数据添加到示例元数据中。这是直截了当的博斯 alpha_diversity 还一只Pandas Series 对象,我们在Pandas中表示我们的示例元数据 DataFrame 对象。
>>> sample_md['Observed OTUs'] = adiv_obs_otus
>>> sample_md['Faith PD'] = adiv_faith_pd
>>> sample_md
body_site subject Observed OTUs Faith PD
A gut s1 5 6.75
B skin s1 5 7.00
C tongue s1 4 6.25
D gut s2 4 5.75
E tongue s2 5 6.75
F skin s2 3 5.50
我们可以在元数据类别的上下文中研究这些alpha多样性数据。例如,我们可以生成按身体部位显示Faith PD的箱线图。
>>> import matplotlib.pyplot as plt
>>> plt.close('all') # not necessary for normal use
>>> fig = sample_md.boxplot(column='Faith PD', by='body_site')
(Source code, png)
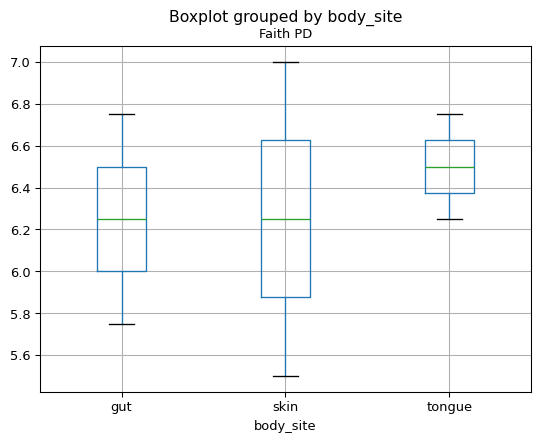
我们也可以计算所有列对之间的Spearman相关性 DataFrame . 因为我们的alpha多样性度量是仅有的两个数字列(因此也是唯一与Spearman相关的列),这将给我们一个对称的2x2相关矩阵。
>>> sample_md.corr(method="spearman", numeric_only=True)
Observed OTUs Faith PD
Observed OTUs 1.000000 0.939336
Faith PD 0.939336 1.000000
