Tsetlin库

引言

在本节中，我们学习一种简单的随机游走(或称马尔可夫链)，称为 Tsetlin library 。它将使我们有机会看到组合学、线性代数、表示理论和计算机探索之间的相互作用，而不需要大量的理论背景。我希望这会鼓励每个人玩弄这个或类似的系统，调查他们的财产！形式定理和证明可以在本节末尾的参考文献中找到。

众所周知，群表示理论可以方便地研究演化是随机的系统(马尔可夫链)，将它们分解成更简单的系统。最近，人们意识到，推广这一点(即用其他公理取代群的可逆性公理)解释了其他特别简单的马尔可夫链的行为，如Tsetlin库。

Tsetlin库

假设类库里有一个书架，里面有 n 各式各样的书。当一个人借了一本书，然后又归还了它，它就会被放回书架上，放在所有书的右边。这是我们自然而然地处理衣柜里的一堆衬衫的方式：在使用和清洗之后，衬衫被放在它的一堆衣服的顶部。因此，最受欢迎的书/衬衫更有可能出现在书架/书堆的右边/顶部。

这种类型的组织具有自适应的优势：

  • 最常用的书堆积在右边，因此很容易找到。

  • 如果使用随着时间的推移而改变，系统就会适应。

事实上，这种策略不仅在日常生活中使用，在计算机科学中也是如此。随之而来的自然问题是：

  • Stationary distribution ：系统收敛到什么状态(S)？在其他方面，这是用来评估一本书的平均访问时间的。

  • The rate of convergence 系统适应不断变化的环境的速度有多快？

让我们形式化地描述一下。Tsetlin库是离散马尔可夫链(离散时间、离散状态空间)，其描述如下：

  • 状态空间 Omega_n 的所有排列的集合给出 n 书。

  • The transition operators are denoted by partial_i colon Omega_n to Omega_n. When partial_i is applied to a permutation sigma, the number i is moved to the end of the permutation.

  • We assign parameters x_i ge 0 for all 1le ile n with sum_{i=1}^n x_i = 1. The parameter x_i indicates the probability of choosing the operator partial_i.

转移图和转移矩阵

One can depict the action of the operators partial_i on the state space Omega_n by a digraph. The following picture shows the action of partial_1, partial_2, partial_3 on Omega_3:

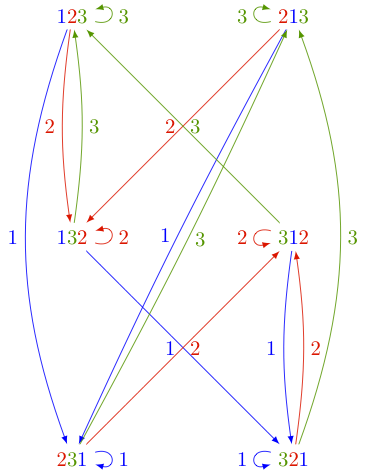
../_images/tsetlin-library.png

上述图片可在Sage中转载如下：

sage: P = Poset(([1,2,3],[]))

这是反链偏序集。它的线性扩张都是 {1,2,3} **

sage: L = P.linear_extensions()
sage: L
The set of all linear extensions of Finite poset containing 3 elements
sage: L.list()
[[3, 2, 1], [3, 1, 2], [1, 3, 2], [1, 2, 3], [2, 1, 3], [2, 3, 1]]

该图表通过以下方式生成：

sage: G = L.markov_chain_digraph(labeling='source'); G
Looped multi-digraph on 6 vertices
sage: view(G)  # not tested

现在我们可以查看转换矩阵，并查看是否注意到其特征值和特征向量的任何内容：

sage: M = L.markov_chain_transition_matrix(labeling='source')
sage: M
[-x0 - x1       x2        0        0       x2        0]
[      x1 -x0 - x2       x1        0        0        0]
[       0        0 -x0 - x1       x2        0       x2]
[      x0        0       x0 -x1 - x2        0        0]
[       0        0        0       x1 -x0 - x2       x1]
[       0       x0        0        0       x0 -x1 - x2]

该矩阵被规格化，因此所有列的总和为0。因此，我们需要添加 (x_0 + x_1 + x_2) 泰晤士报 6times 6 单位矩阵，以获取概率矩阵：：

sage: x = M.base_ring().gens()
sage: Mt = (x[0]+x[1]+x[2])*matrix.identity(6)+M
sage: Mt
[x2 x2  0  0 x2  0]
[x1 x1 x1  0  0  0]
[ 0  0 x2 x2  0 x2]
[x0  0 x0 x0  0  0]
[ 0  0  0 x1 x1 x1]
[ 0 x0  0  0 x0 x0]

自.以来 x_i 都是形式变量，我们需要计算符号环上的特征值和特征向量 SR **

sage: Mt.change_ring(SR).eigenvalues()
[x2, x1, x0, x0 + x1 + x2, 0, 0]

你看到什么图案了吗？事实上，如果你开始尝试更大的价值 n (基础排列的大小)，您可能会注意到每个子集都有一个特征值 S 的 {1,2,ldots,n} 并且重数由一个错位数给出 d_{n-|S|} 。乱序数计算没有固定点的排列。对于特征向量，我们得到：：

sage: Mt.change_ring(SR).eigenvectors_right()
[(x2, [(1, 0, -1, 0, 0, 0)], 1),
 (x1, [(0, 1, 0, 0, -1, 0)], 1),
 (x0, [(0, 0, 0, 1, 0, -1)], 1),
 (x0 + x1 + x2,
  [(1,
    (x0 + x1)/(x0 + x2),
    x0/x1,
    (x0^2 + x0*x1)/(x1^2 + x1*x2),
    (x0^2 + x0*x1)/(x0*x2 + x2^2),
    (x0^2 + x0*x1)/(x1*x2 + x2^2))], 1),
 (0, [(1, 0, -1, 0, -1, 1), (0, 1, -1, 1, -1, 0)], 2)]

平稳分布是特征值的特征向量 1=x_0+x_1+x_2 。你看到模式了吗？

结论

从么半群的观点研究了Tsetlin文库 [Bidigare1997] 和 [Brown2000]. 文中给出了概率矩阵的特征值和平稳分布的精确表述以及表述的证明。中给出了从反链到任意偏序集的Tsetlin库的推广 [AKS2013].

[Bidigare1997]

托马斯·帕特里克·比迪盖尔。 Hyperplane arrangement face algebras and their associated Markov chains 。ProQuest LLC，密西西比州安娜堡，1997年。论文(博士学位)密歇根大学。

[Brown2000]

肯尼斯·S·布朗 Semigroups, rings, and Markov chains 。J.Theoret。可能，13(3)：871-938,2000。

[AKS2013]

阿文德·艾耶，史蒂文·克利，安妮·希林。 Combinatorial Markov chains on linear extensions J·代数组合学， :doi:`10.1007/s10801-013-0470-9` ， :arxiv:`1205.7074` 。