n -多维数据集

这一部分提供了斯坦利书中第二章的一些例子 [Stanley2013], 它处理的是 n -立方体、Radon变换和行走的组合公式 n -立方体。

的顶点 n -立方体可以用向量来描述 mathbb{Z}_2^n 。首先，我们定义了两个向量的相加 u,v in mathbb{Z}_2^n 通过以下距离：

sage: def dist(u,v):
....:     h = [(u[i]+v[i])%2 for i in range(len(u))]
....:     return sum(h)

距离函数测量两个向量在多少个槽中 mathbb{Z}_2^n 不同：：

sage: u = (1,0,1,1,1,0)
sage: v = (0,0,1,1,0,0)
sage: dist(u,v)
2

现在，我们将定义 n -立方体作为包含顶点的图 mathbb{Z}_2^n 和顶点之间的边 u 和顶点 v 如果它们在一个插槽中不同，即距离函数为1：：

sage: def cube(n):
....:     G = Graph(2**n)
....:     vertices = Tuples([0,1],n)
....:     for i in range(2**n):
....:         for j in range(2**n):
....:             if dist(vertices[i],vertices[j]) == 1:
....:                 G.add_edge(i,j)
....:     return G

我们可以画出 3 和 4 -立方体：：

sage: cube(3).plot()
Graphics object consisting of 21 graphics primitives
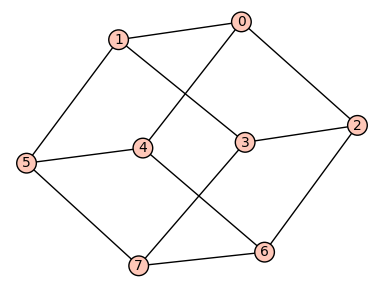
../_images/cube3.png 
sage: cube(4).plot()
Graphics object consisting of 49 graphics primitives
../_images/cube4.png

接下来，我们可以试验和检验斯坦利书中的推论2.4，该书指出 n -立方体有 n 选择 i 本征值等于 n-2i **

sage: G = cube(2)
sage: G.adjacency_matrix().eigenvalues()
[2, -2, 0, 0]

sage: G = cube(3)
sage: G.adjacency_matrix().eigenvalues()
[3, -3, 1, 1, 1, -1, -1, -1]

sage: G = cube(4)
sage: G.adjacency_matrix().eigenvalues()
[4, -4, 2, 2, 2, 2, -2, -2, -2, -2, 0, 0, 0, 0, 0, 0]

现在，通过连接折点可以很容易地略微更改此问题并更改边集 u 和 v 如果它们的距离为2(参见第2章中的问题4)：

sage: def cube_2(n):
....:     G = Graph(2**n)
....:     vertices = Tuples([0,1],n)
....:     for i in range(2**n):
....:         for j in range(2**n):
....:             if dist(vertices[i],vertices[j]) == 2:
....:                 G.add_edge(i,j)
....:     return G

sage: G = cube_2(2)
sage: G.adjacency_matrix().eigenvalues()
[1, 1, -1, -1]

sage: G = cube_2(4)
sage: G.adjacency_matrix().eigenvalues()
[6, 6, -2, -2, -2, -2, -2, -2, 0, 0, 0, 0, 0, 0, 0, 0]

请注意，该图实际上是断开的。你明白为什么吗？

sage: cube_2(4).plot()
Graphics object consisting of 65 graphics primitives
../_images/cube-dist.png